
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
М.8.7. Какие безразмерные координаты приняты в нормах (СНиП) для расчета напряжений?
Для расчета напряжений в нормах (СНиП) приняты две относительные координаты x и h, причем М.8.8. При каком значении Считается, что при h = 10 мы имеем значения напряжений s z, которыми для практических целей можно пользоваться и в случае плоской деформации, то есть когда следовало бы считать h =¥. М.8.9. Каким образом, зная эпюру напряжений s z вдоль оси z при равномерно распределенной нагрузке, действующей на участке шириной b, построить эпюру s z, если нагрузка будет действовать в пределах участка шириной 2 b? Как будет трансформироваться эпюра s z при дальнейшем увеличении ширины участка, в пределах которого она приложена? Если имеется эпюра напряжений s z при ширине загруженного участка b, то, зная ординату s z на глубине z, нужно эту же ординату для случая ширины 2 b отложить на глубине 2 z и т.д. (рис.М.8.9).
При дальнейшем росте ширины загруженного участка напряжения будут все медленнее рассеиваться и при увеличении b до бесконечности эпюра s z будет иметь постоянную ординату s z = p. Все эти эпюры имеют верхнюю ординату, равную p, и выходят поэтому из одной точки.
М.8.11. Каким образом влияет на эпюру s z при местной нагрузке наличие жесткого подстилающего слоя? В нижней части эпюры напряжений s z, построенных для оси симметрии, вблизи границы жесткого подстилающего слоя происходит так называемая "концентрация" напряжений, то есть их увеличение по сравнению с эпюрой для безграничного снизу слоя (полупространства). Эта концентрация напряжений имеет местное значение и с удалением от границы жесткого подстилающего слоя сравнительно быстро убывает (рис.М.8.11).
М.8.12. Каким образом распределяются напряжения s z под подошвой жесткого штампа? Чему равны реактивные напряжения под краем штампа? Чему равны реактивные напряжения под серединой ленточного и круглого жестких штампов?
В соответствии с решением задачи об абсолютно жестком штампе, плотно примыкающем к поверхности упругого полупространства и нагруженном симметричной нагрузкой, эпюра реактивных давлений имеет седлообразное очертание с минимальной ординатой в середине и наибольшими ординатами реактивных давлений, равными бесконечности, у краев. Эти бесконечно большие давления у краев штампа вызывают необходимый из постановки задачи "излом" поверхности в краевых точках. Если среднее давление под подошвой штампа равно p, то под серединой ленточного штампа ордината эпюры равна 0,637 p (то есть 2 p /p), а под круглым штампом 0,5 p (рис.М.8.12). М.8.13*. Что следует сделать, чтобы проверить условие равновесия, пользуясь эпюрой реактивных напряжений под подошвой штампа? Для этой цели следует найти объем эпюры реактивных давлений (для плоского штампа на единицу длины), и этот объем должен равняться суммарной внешней нагрузке, действующей на штамп, то есть сумма проекций на вертикальную ось действующих сил должна равняться нулю (условие равновесия). М.9. РАСЧЕТ ДЕФОРМАЦИЙ ОСНОВАНИЙ СООРУЖЕНИЙ
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.128.129 (0.005 с.) |
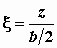 и
и  , где b - ширина (наименьшая сторона) подошвы прямоугольного фундамента, l - его длина (всегда l³ b).
, где b - ширина (наименьшая сторона) подошвы прямоугольного фундамента, l - его длина (всегда l³ b).
 Рис.М.8.10. Изменение эпюры s z в случае пространственной задачи при постоянной ширине загруженного участка и изменении его длины
Рис.М.8.10. Изменение эпюры s z в случае пространственной задачи при постоянной ширине загруженного участка и изменении его длины





