
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые законы распределения случайных величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
5.1. Биноминальное распределение. 5.2. Распределение Пуассона. 5.3. Равномерное распределение. 5.4. Нормальное распределение.
Биноминальное распределение Пусть производится п независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна р (следовательно, непоявления q = 1 – p. Рассмотрим в качестве дискретной случайной величины X число появлений события А в этих испытаниях. Поставим перед собой задачу: найти закон распределения величины X. Для ее решения требуется определить возможные значения X и их вероятности. Очевидно, событие А в п испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза,..., либо п раз. Таким образом, возможные значения X таковы: х1 = 0, x2 = 1, x3 = 2,..., xn+1= n. Остается найти вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли:
где k = 0, 1, 2,.... п. Данная формула и является аналитическим выражением искомого закона распределения. Биноминальным называют закон распределения дискретной случайной величины
где Таким образом, первый член разложения рп определяет вероятность наступления рассматриваемого события п раз в п независимых испытаниях; второй член Напишем биномиальный закон в виде таблицы:
При этом математическое ожидание и дисперсия соответственно равны:
Пример5.1. Монета брошена 2 раза. Написать в виде таблицы закон распределения случайной величины X — числа выпадений «герба». Решение. Вероятность появления «герба» в каждом бросании монеты При двух бросаниях монеты «герб» может появиться либо 2 раза, либо 1 раз, либо совсем не появиться. Таким образом, возможные значения X таковы: x1 = 2, х2 = 1, х3 = 0. Найдем вероятности этих возможных значений по формуле Бернулли:
Напишем искомый закон распределения:
Контроль: 0,25 + 0,5 + 0,25 = 1.
Распределение Пуассона. Пусть производится п независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна р (следовательно, непоявления q = 1 – p. Рассмотрим в качестве дискретной случайной величины X число появлений события А в этих испытаниях. Поставим перед собой задачу: найти закон распределения величины X. Если число испытаний велико, а вероятность появления события
где
Случайная величина, характеризующая число наступлений события
Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона:
Замечание. Имеются специальные таблицы, пользуясь которыми можно найти Пример 5.2. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равно 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия. Решение. По условию, п = 5000, р = 0,0002, k = 3. Найдем
По формуле Пуассона искомая вероятность приближенно равна:
Равномерное распределение Распределение вероятностей случайной величины Х называется равномерным на отрезке Выражение плотности распределения вероятностей
Функция равномерного распределения задается формулой:
Напомним, что вероятность попадания значений случайной величины Х в интервал
Математическое ожидание, дисперсия и среднее квадратическое отклонение соответственно равны:
Нормальное распределение. Распределение с непрерывной случайной величины называется нормальным, если плотность распределения ее описывается формулой:
где Функция распределения случайной величины Х, распределенной по нормальному закону:
Полученный интеграл нельзя выразить через элементарные функции, но его можно вычислить через специальную функцию:
называемую нормальной функцией распределения (функцией Лапласа). Эта функция неубывающая, непрерывная и Вероятность попадания случайной величины
где Замечание. Имеются специальные таблицы, пользуясь которыми можно найти значения функции Лапласа (Приложение 1).
Вероятность заданного отклонения вычисляется по формуле:
Математическое ожидание и дисперсия соответственно равны:
Правило трех сигм: Интервалом практически возможных значений случайной величины
Литература: 1. Гмурман, В. Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов/В. Е. Гмурман. — 9-е изд., стер. — М.: Высш. шк., 2003. — с. 66 – 74. 2. Гусак А.А. Теория вероятностей: справ. Пособие к решению задач / А.А. Гусак, Е.А. Бричикова. – 6-е изд. – Минск: ТетраСистемс, 2007. – с. 184 – 244. Контрольные вопросы: 1. Какое распределение случайной величины называется нормальным? 2. Какое распределение случайной величины называют биноминальным? 3. Какое распределение случайной величины называют равномерным? 4. Какое распределение называют распределением Пуассона?
Задания для самостоятельного решения Задание 5.1. В партии из шести деталей имеется четыре стандартных. Наудачу отобраны три детали. Составить закон распределения дискретной случайной величины X — числа стандартных деталей среди отобранных. Задание 5.2. Коробки с шоколадом упаковываются автоматически: средняя масса одной коробки – 1,06 кг. Известно, что только 5% коробок имеют массу меньше 1 кг. Найти стандартное отклонение, предполагая, что масса коробок распределена нормально. Задание 5.3. Найти математическое ожидание случайной величины X, равномерно распределенной в интервале (а, b). Тема 6
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 594; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |

 ,
, - числа появлений событий в
- числа появлений событий в 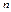 независимых испытаниях, в каждом из которых вероятность появления события равна
независимых испытаниях, в каждом из которых вероятность появления события равна  ; вероятность возможного значения
; вероятность возможного значения  (числа
(числа  появлений события) вычисляют по формуле Бернулли:
появлений события) вычисляют по формуле Бернулли: .
. определяет вероятность наступления события п – 1 раз;...; последний член qп определяет вероятность того, что событие не появится ни разу.
определяет вероятность наступления события п – 1 раз;...; последний член qп определяет вероятность того, что событие не появится ни разу.

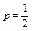 , следовательно, вероятность непоявления «герба»
, следовательно, вероятность непоявления «герба» 



 ,
, – среднее число появлений событий в
– среднее число появлений событий в  в
в 

 , зная k и
, зная k и  (Приложение 2).
(Приложение 2).
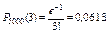
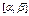 , если плотность вероятности равна нулю всюду, кроме отрезка
, если плотность вероятности равна нулю всюду, кроме отрезка  имеет следующий вид:
имеет следующий вид:




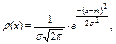
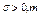 – параметры нормального распределения.
– параметры нормального распределения.


 , определяется следующим образом:
, определяется следующим образом: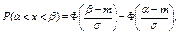
 функция Лапласа.
функция Лапласа.

 .
.


