
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегральная теорема ЛапласаСодержание книги
Поиск на нашем сайте
Предположим, что производится п испытаний, в каждом из которых вероятность появления события А постоянна и равна р (0 < р < 1). Как вычислить вероятность На этот вопрос отвечает интегральная теорема Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность
где При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами (Приложение 2), так как неопределенный интеграл не Функцию Ф(х) часто называют функцией Лапласа. Для того чтобы можно было пользоваться таблицей функции Лапласа, выполним следующие преобразования:
Итак, вероятность того, что событие А появится в п независимых испытаниях от
где
Пример 3.5. Вероятность того, что деталь не прошла проверку ОТК, равна р = 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей. Решение. По условию, р = 0,2; q = 1 – p = 0,8; n = 400; Воспользуемся интегральной теоремой Лапласа:
Вычислим нижний и верхний пределы интегрирования:
Таким образом, имеем
По таблице находим:
Искомая вероятность равна:
Литература: 1. Гмурман, В. Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов/В. Е. Гмурман. — 9-е изд., стер. — М.: Высш. шк., 2003. — с.55 – 61. 2. Гусак А.А. Теория вероятностей: справ. Пособие к решению задач / А.А. Гусак, Е.А. Бричикова. – 6-е изд. – Минск: ТетраСистемс, 2007. – с.173 – 184. Контрольные вопросы: 1. Какой вид имеет формула Бернулли? 2. Каким должны быть события, чтобы можно было применить формулу Бернулли? 3. Как вычислить вероятность того, что в nнезависимых испытаниях событие наступит: а) менее k раз; б) более k раз; в) от k1 раз до k2 раз?
Задания для самостоятельного решения Задание 3.1. Монету бросают пять раз. Найти вероятность того, что «герб» выпадет: а) менее двух раз; б) не менее двух раз. Задание 3.2. В семье пять детей. Найти вероятность того, что среди этих детей: а) два мальчика; б) не более двух мальчиков; в) более двух мальчиков; г) не менее двух и не более трех мальчиков. Вероятность рождения мальчика принять равной 0,51. Задание 3.3. Найти вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25. Тема 4 Случайные величины
4.1. Понятие случайной величины. 4.2. Виды случайных величин. 4.3. Закон распределения вероятностей дискретной случайной величины. 4.4. Функция распределения. 4.5. Математическое ожидание случайной величины. 4.6. Дисперсия случайной величины. Среднее квадратическое отклонение.
Понятие случайной величины Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены. Пример 4.1. Расстояние, которое пролетит снаряд при выстреле из орудия, есть случайная величина. Действительно, расстояние зависит не только от установки прицела, но и от многих других причин (силы и направления ветра, температуры и т. д.), которые не могут быть полностью учтены. Возможные значения этой величины принадлежат некоторому промежутку (а, b). Пример 4.2. Число родившихся мальчиков среди ста новорожденных есть случайная величина, которая имеет следующие возможные значения: 0, 1, 2,..., 100. Будем обозначать случайные величины прописными буквами X, Y, Z, а их возможные значения – соответствующими строчными буквами. Пример 4.3. Если случайная величина X имеет три возможных значения, то они будут обозначены так: х1, х2, х3.
Виды случайных величин. В примере 4.2 случайная величина X могла принять одно из следующих возможных значений: 0, 1, 2,..., 100. Эти значения отделены одно от другого промежутками, в которых нет возможных значений X. Таким образом, в этом примере случайная величина принимает отдельные, изолированные возможные значения. В примере 4.1 случайная величина могла принять любое из значений промежутка (а, b). Здесь нельзя отделить одно возможное значение от другого промежутком, не содержащим возможных значений случайной величины. Уже из сказанного можно заключить о целесообразности различать случайные величины, принимающие лишь отдельные, изолированные значения, и случайные величины, возможные значения которых сплошь заполняют некоторый промежуток. Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным. Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.99.221 (0.008 с.) |

 того, что событие А появится в п испытаниях не менее
того, что событие А появится в п испытаниях не менее  и не более
и не более  раз?
раз?

 и
и 
 не выражается через элементарные функции. В таблице даны значения функции Ф(х) для положительных значений х и для х = 0; для х < 0 пользуются той же таблицей (функция Ф(х) нечетна, т. е. Ф(–х) = – Ф(х)) В таблице приведены значения интеграла лишь до х = 5, так как для х > 5 можно принять Ф (х) = 0,5.
не выражается через элементарные функции. В таблице даны значения функции Ф(х) для положительных значений х и для х = 0; для х < 0 пользуются той же таблицей (функция Ф(х) нечетна, т. е. Ф(–х) = – Ф(х)) В таблице приведены значения интеграла лишь до х = 5, так как для х > 5 можно принять Ф (х) = 0,5.
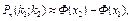
 и
и  = 70;
= 70;  =100.
=100.








