Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайные события и вероятностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В.П. Кошелева
«Теория вероятностей и Математическая статистика» (пособие для учащихся) Теория вероятности - это математическая наука, изучающая закономерности в случайных явлениях. Достоверным называют событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий S. Например, если в сосуде содержится вода при нормальном атмосферном давлении и температуре 20о, то событие ввода в сосуде находится в жидком состоянии? есть достоверное. В этом примере заданные атмосферное давление и температура воды составляют совокупность условий S. Невозможным называют событие, которое заведомо не произойдет, если будет осуществлена совокупность условий S. Например, событие вода в сосуде находится в твердом состоянии заведомо не произойдет, если будет осуществлена совокупность условий S из предыдущего примера(20о, нормальное атмосферное давление). Случайным называют событие, которое при осуществлении совокупности условий S может либо произойти, либо не произойти. Например, если брошена монет она может упасть вверх гербом или вверх надписью. Поэтому событие при бросании монеты выпал герб - случайное. Каждое случайное событие, в частности выпадение герба, есть следствие действия многих случайных причин (сила с которой брошена монета, форма монеты, вес и т.д.). Не возможно учесть влияние этих причин на результат, по сколку их число очень велико, по этому теория вероятностей не ставит перед собой задачу предсказать. Произойдет единичное событие или нет. По-иному обстоят дело, если рассматривать случайные события, которые могут многократно наблюдаться при осуществлении одних и тех же условий S, то есть если речь идет о массовых однородных случайных событиях. Оказывается, что достаточно большое число однородных случайных событий независимо от их конкретной природы подчиняется определенным закономерностям. Установлением этих закономерностей и занимается теория вероятностей. Следовательно, предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных событий. Знание закономерностей, которым подчиняются массовые случайные события, позволяет предвидеть, как эти события будут протекать. Методы теории вероятностей широко применяются в различных отраслях естествознания и техники: в теории надежности, теории массового обслуживания, в теоретической физике, геодезии, астрономии, теории автоматического управления и во многих других теоретических и прикладных науках. Теория вероятностей служит также для обоснования математической и прикладной статистики, которая в свою очередь используется при планировании и организации производства, при анализе технологических процессов, предупредительном и приемочном контроле качества продукции и для многих других целей. В последние годы методы теории вероятностей все шире и шире проникают в различные области науки и техники, способствуя их прогрессу. Тема 1 Элементы комбинаторики 1.1. Предмет комбинаторики. 1.2. Правила комбинаторики (сложения и произведения). 1.3. Понятие факториала. 1.4. Перестановки. 1.5. Размещения. 1.6. Сочетания. 1.1. Предмет комбинаторики Комбинаторика – это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания. Слово «комбинаторика» происходит от латинского combino — соединяю. Действительно, при получении любой комбинации мы составляем ее из отдельных элементов, последовательно соединяя их друг с другом. Чаще всего эти элементы выбираются из некоторого конечного множества.
Правила комбинаторики Подсчитать общее число возможных комбинаций помогает одно из важнейших правил комбинаторики — правило умножения: если первый элемент в комбинации можно выбрать m способами, после чего второй элемент — n способами, то общее число комбинаций из двух элементов будет m · n. Пример 1.1. Подсчитаем количество двузначных чисел, которые можно составить из цифр 1, 2, 3. На первое место цифру можно выбрать тремя способами, после чего на второе место — тоже тремя способами. Значит, всего таких чисел по правилу умножения будет 3 · 3 = 9. Можно проверить ответ, выписав друг за другом все эти числа в порядке возрастания: 11, 12, 13; 21, 22, 23; 31, 32, 33. В приведенном примере выбор второй цифры никак не связан с выбором первой. Но это далеко не всегда так. Пример 1.2. Подсчитаем количество двузначных чисел, которые можно составить из цифр 1, 2, 3 так, чтобы все цифры были различны. На первое место цифру можно выбрать тремя способами, после чего на второе место — только двумя способами (ту цифру, которая на первом месте, использовать уже нельзя). Значит, всего таких чисел по правилу умножения будет 3 · 2 = 6. Вот эти числа: 12, 13; 21, 23; 31, 32. Теперь в каждой из трех групп только по два элемента. В данных примерах две принципиально различные схемы выбора элементов: а) без возращения (повторений) элементов (это значит, что отбираются либо сразу все б ) с возвращением (повторением) элементов (выбор осуществляется поэлементно с обязательным возвращением отобранного элемента на каждом шаге и тщательном перемешиванием исходного множества перед следующим выбором). Но бывают задачи, в которых после выбора одного из m объектов в качестве первого элемента комбинации нельзя однозначно сказать, сколькими способами можно выбрать второй элемент — это зависит от того, какой именно объект был выбран первым. Рассмотрим такую ситуацию на примере. Пример 1.3. Подсчитаем количество двузначных чисел, которые можно составить из цифр 1, 2, 3 так, чтобы первая цифра была меньше второй. На первое место цифру можно выбрать тремя способами, а вот на второе место после этого: – двумя способами, если первой цифрой была выбрана 1; – одним способом, если 2; – нулем способов, если 3. Приходится применять комбинаторное правило сложения: разбить все комбинации на непересекающиеся классы, подсчитать количество комбинаций в каждом классе (например, по правилу умножения), а затем сложить эти количества. В предыдущем примере количество комбинаций равно: 2 + 1 = 3. Понятие факториала п -факториал - произведение всех натуральных чисел от 1 до п включительно.
Пример 1.4. 1) 2) Следует отметить, что 0! = 1. Перестановки Перестановки – комбинации из n элементов, которые отличаются друг от друга только порядком элементов. Общее число перестановок из n элементов обозначается
Пример 1.5. Из букв A, B, C можно составить следующие перестановки: ABC, ACB, BAC, BCA, CAB, CBA. Всего перестановок Пример 1.6. Сколькими способами можно расставить на книжной полке собрание сочинений Диккенса, включающее 30 томов? Решение: Каждый такой способ — это перестановка из 30 элементов. Всего таких перестановок будет
Число перестановок с повторениями можно найти применив формулу:
Размещения Размещения – комбинации из n элементов по m элементов, которые отличаются друг от друга или самими элементами или их порядком. Размещения обозначаются где n – числи всех имеющихся элементов, m – число элементов к каждой комбинации. При этом полагают, что
Пример 1.7. Пусть имеются четыре буквы А, В, С, D. Составив все комбинации только из двух букв, получим: АВ, АС, АD, ВА, ВС, ВD, СА, СВ, СD, DA, DB, DC. Все полученные комбинации отличаются или буквами, или порядком (комбинации ВА и АВ считаются различными). Кратко это можно записать так:
Пример 1.8. На книжную полку влезает только 8 любых томов из 30-томного собрания Диккенса. Сколькими способами можно заполнить этими томами такую полку? Решение: Каждый способ — это размещение из 30 элементов по 8. Всего таких размещений будет
Число размещений с повторениями равно:
Сочетания Сочетания – все возможные комбинации из n элементов по m элементов, которые отличаются друг от друга по крайней мере хотя бы одним элементом. Сочетания обозначаются
Пример 1.9. Из четырех различных букв А, В, С, D можно составить следующие комбинации, отличающиеся друг от друга хотя бы одним элементом: АВ, АС, АD, ВС, ВD, СD. Значит число сочетаний из четырех элементов по два равно 6. Это можно найти и по вышеприведенной формуле:
Для сочетаний справедливы равенства:
Число перестановок, размещений и сочетаний связаны равенством:
Литература: 1. Гмурман, В. Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов/В. Е. Гмурман. — 9-е изд., стер. — М.: Высш. шк., 2003. — с.22 – 23. 2. Гусак А.А. Теория вероятностей: справ. Пособие к решению задач / А.А. Гусак, Е.А. Бричикова. – 6-е изд. – Минск: ТетраСистемс, 2007. – с.13 – 21. Контрольные вопросы: 1. В чем сущность комбинаторики? 2. Сформулируйте правило сложения. 3. Сформулируйте правило умножения. 4. В чем отличие выбора элементов с возращениями и без возращений? 5. Что называют перестановками? 6. По какой формуле вычисляют число перестановок из п различных элементов? 7. По какой формуле вычисляют число перестановок из п различных элементов с повторениями? 8. Что называют размещениями? 9. По какой формуле вычисляют число размещений из п различных элементов по m элементов? 10. Что называют сочетаниями? 11. По какой формуле вычисляют число сочетаний из элементов п различных элементов по m элементов? 12. Каким равенством связаны числа перестановок, размещений и сочетаний? 13. Чем отличаются сочетания от размещений? Что и во сколько раз больше?
Задания для самостоятельного решения Задание 1.1. Упростить: а) Задание 1.2. Вычислить: а) Задание 1.3. Вычислить: а) Задание 1.4. Вычислить: а) Задание 1.5. Докажите равенство, связывающее между собой числа перестановок, размещений и сочетаний. Задание 1.6. В автомобиле 5 мест. Сколькими способами пять человек могут занять места для путешествия, если водить машину могут только трое из них. Задание 1.7. После хоккейного матча каждый игрок одной команды пожал руку каждому игроку другой. Сколько всего игроков присутствовало на площадке, если было совершено 323 рукопожатия?
Тема 2 Понятие случайного события Виды случайных событий События,которые никогда не могут произойти называется невозможными. События, которые происходят при каждом экспериментеназываются достоверны ми. Пример 2.3. Событие А - «на игральном кубике выпадет 7 очков» — невозможное, а событие В – «на игральном кубике выпадет меньше семи очков» — достоверное. Разумеется, если речь идет о кубике, на гранях которого написаны числа от 1 до 6. Два события называются несовместными, если они не могут произойти вместе при одном и том же испытании. В противном случае события называются совместными. Пример 2.4. Несовместными являются попадание и промах при одном выстреле. Два события называются противоположными, если появление одного из них равносильно непоявлению другого. Если одно из противоположных событий обозначено буквой А, то другое обозначают Пример 2.5. Если событие А – «попадание», то событие мишени. Несколько событий в условиях данного опыта образуют полную группу событий, если в результате опыта произойдет обязательно хотя бы одно из них. Пример 2.6. Учащемуся на экзамене достался билет с двумя теоретическими вопросами. События А1 – «учащийся знает оба вопроса», А2 – «учащийся знает первый вопрос, но не знает второго», А3 – «учащийся знает второй вопрос, но не знает первого», А4 – «учащийся знает только один вопрос», А5 – «учащийся не знает ни одного вопроса» образуют полную систему событий, среди которых имеются как несовместные А1 и А2, А1 и А5 и другие, так и совместные А2 и А4, А3 и А4. Различают события элементарные и составные. Так, в примере 2.6 событие А4 является составным событием из А2 и А3, поэтому событие А4 наступит только в результате наступления либо только элементарного события А2, либо только элементарного события А3. В таком случае говорят, что событие А4 разлагается на элементарные события А2 и А3, и пишут А4 = {А2, А3}. События называются равновозможными, если условия испытания обеспечивают одинаковую возможность осуществления каждого из них. Пример 2.7. При подбрасывании монеты событие А – «появление орла» и событие В – «появление решки» равновозможны, так как предполагается, что монета изготовлена из однородного материала, имеет правильную цилиндрическую форму и наличие чеканки не влияет на то, какая сторона монеты окажется верхней. Операции над событиями Дадим определения действий, которые можно производить над событиями. Если при всяком испытании, при котором происходит событие А, происходит и событие B, то событие А называется частным случаем события B. Говорят также, что А влечет за собой B и пишут: А Ì B или B É A. Пример 2.10. При бросании игральной кости событие А, состоящее в появлении двух очков, есть частный случай события B, состоящего в появлении четного числа очков. Если А влечет за собой B, а B влечет за собой А, то эти события равносильны, так как они вместе наступают или вместе не наступают. Суммой двух событий A и B называется событие A+B (AÈB), состоящее из элементарных событий, принадлежащих хотя бы одному из событий A или B. Пример 2.11. Суммой событий А – «появление одного очка при бросании игральной кости» и события В – «появление двух очков при бросании игральной кости» является событие А + В – «появление не больше двух очков при бросании игральной кости» Произведением двух событий A и B называется событие AB (AÇB), состоящих из элементарных событий, принадлежащих одновременно A и B. Пример 2.12. Если событие А – «деталь годная», событие В – «деталь окрашенная», то событие АВ – «деталь годна и окрашена». Разностью двух событий A и B называют событие A\B, состоящее из элементарных событий, которые входят в событие B. Операции над событиями подчинены следующим правилам:
Тема 3 Повторные испытания
3.1. Формула Бернулли. 3.2. Локальная теорема Лапласа. 3.3. Интегральная теорема Лапласа.
Формула Бернулли Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А. Пусть производится п независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Условимся считать, что вероятность события А в каждом испытании одна и та же, а именно равна р. Следовательно, вероятность ненаступления события А в каждом испытании также постоянна и равна q = 1– р. Поставим перед собой задачу вычислить вероятность того, что при п испытаниях событие А осуществится ровно k раз и, следовательно, не осуществится п – k раз. Важно подчеркнуть, что не требуется, чтобы событие А повторилось ровно k раз в определенной последовательности. Пример 3.1. Если речь идет о появлении события А три раза в четырех испытаниях, то возможны следующие сложные события:
Искомую вероятность обозначим Рп(k). Пример 3.2. Символ Поставленную задачу можно решить с помощью так называемой формулы Бернулли.
или
Пример 3.3. Вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной нормы, равна р = 0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы. Решение. Вероятность нормального расхода электроэнергии в продолжение каждых из 6 суток постоянна и равна р = 0,75. Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна q = 1 – 0,75 = 0,25. Искомая вероятность по формуле Бернулли равна:
Локальная теорема Лапласа Пользоваться формулой Бернулли при больших значениях п достаточно трудно, так как формула требует выполнения действий над громадными числами. Например, если п = 50, k = 30, р = 0,1, то для отыскания вероятности где
Правда, можно несколько упростить вычисления, пользуясь специальными таблицами логарифмов факториалов. Однако и этот путь остается громоздким и к тому же имеет существенный недостаток: таблицы содержат приближенные значения логарифмов, поэтому в процессе вычислений накапливаются погрешности; в итоге окончательный результат может значительно отличаться от истинного. Естественно возникает вопрос: нельзя ли вычислить интересующую нас вероятность, не прибегая к формуле Бернулли? Оказывается, можно. Локальная теорема Лапласа и дает формулу, которая позволяет приближенно найти вероятность появления события ровно k раз в п испытаниях, если число испытаний достаточно велико. Локальная теорема Лапласа. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность
при Имеются таблицы (Приложение 1), в которых помещены значения функции
Итак, вероятность того, что событие А появится в п независимых испытаниях ровно k раз, приближенно равна:
где Пример 3.4. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2. Решение. По условию, n = 400; k = 80; р = 0,2; q = 1 – 0,8. Воспользуемся формулой Лапласа:
Вычислим определяемое данными задачи значение х:
По таблице находим Искомая вероятность
Тема 4 Случайные величины
4.1. Понятие случайной величины. 4.2. Виды случайных величин. 4.3. Закон распределения вероятностей дискретной случайной величины. 4.4. Функция распределения. 4.5. Математическое ожидание случайной величины. 4.6. Дисперсия случайной величины. Среднее квадратическое отклонение.
Понятие случайной величины Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены. Пример 4.1. Расстояние, которое пролетит снаряд при выстреле из орудия, есть случайная величина. Действительно, расстояние зависит не только от установки прицела, но и от многих других причин (силы и направления ветра, температуры и т. д.), которые не могут быть полностью учтены. Возможные значения этой величины принадлежат некоторому промежутку (а, b). Пример 4.2. Число родившихся мальчиков среди ста новорожденных есть случайная величина, которая имеет следующие возможные значения: 0, 1, 2,..., 100. Будем обозначать случайные величины прописными буквами X, Y, Z, а их возможные значения – соответствующими строчными буквами. Пример 4.3. Если случайная величина X имеет три возможных значения, то они будут обозначены так: х1, х2, х3.
Виды случайных величин. В примере 4.2 случайная величина X могла принять одно из следующих возможных значений: 0, 1, 2,..., 100. Эти значения отделены одно от другого промежутками, в которых нет возможных значений X. Таким образом, в этом примере случайная величина принимает отдельные, изолированные возможные значения. В примере 4.1 случайная величина могла принять любое из значений промежутка (а, b). Здесь нельзя отделить одно возможное значение от другого промежутком, не содержащим возможных значений случайной величины. Уже из сказанного можно заключить о целесообразности различать случайные величины, принимающие лишь отдельные, изолированные значения, и случайные величины, возможные значения которых сплошь заполняют некоторый промежуток. Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным. Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно.
Функция распределения. Функция распределения случайной величины
где Плотностью распределения
При этом вероятность попадания значений случайной величины Х в интервал
Иногда вместо термина «функция распределения» используют термин «интегральная функция». Для дискретной случайной величины функции распределения вычисляются по формуле:
График функции распределения дискретной случайной величины имеет ступенчатый вид. Убедимся в этом на примере. Пример 4.6. Закон распределения дискретной случайной величины задан следующей таблицей:
Найти функцию распределения. Решение: При При При При При Итак, функция распределения аналитически может быть записана так:
Изобразим график функции
Рис. 4.2. График функции распределения
Тема 5 Биноминальное распределение Пусть производится п независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна р (следовательно, непоявления q = 1 – p. Рассмотрим в качестве дискретной случайной величины X число появлений события А в этих испытаниях. Поставим перед собой задачу: найти закон распределения величины X. Для ее решения требуется определить возможные значения X и их вероятности. Очевидно, событие А в п испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза,..., либо п раз. Таким образом, возможные значения X таковы: х1 = 0, x2 = 1, x3 = 2,..., xn+1= n. Остается найти вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли:
где k = 0, 1, 2,.... п. Данная формула и является аналитическим выражением искомого закона распределения. Биноминальным называют закон распределения дискретной случайной величины
где Таким образом, первый член разложения рп определяет вероятность наступления рассматриваемого события п раз в п независимых испытаниях; второй член Напишем биномиальный закон в виде таблицы:
При этом математическое ожидание и дисперсия соответственно равны:
Пример5.1. Монета брошена 2 раза. Написать в виде таблицы закон распределения случайной величины X — числа выпадений «герба». Решение. Вероятность появления «герба» в каждом бросании монеты При двух бросаниях монеты «герб» может появиться либо 2 раза, либо 1 раз, либо совсем не появиться. Таким образом, возможные значения X таковы: x1 = 2, х2 = 1, х3 = 0. Найдем вероятности этих возможных значений по формуле Бернулли:
Напишем искомый закон распределения:
Контроль: 0,25 + 0,5 + 0,25 = 1.
Распределение Пуассона. Пусть производится п независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна р (следовательно, непоявления q = 1 – p. Рассмотрим в качестве дискретной случайной величины X число появлений события А в этих испытаниях. Поставим перед собой задачу: найти закон распределения величины X. Если число испытаний велико, а вероятность появления события
где
Случайная величина, характеризующая число наступлений события
Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона:
Замечание. Имеются специальные таблицы, пользуясь которыми можно найти Пример 5.2. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равно 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия. Решение. По условию, п = 5000, р = 0,0002, k = 3. Найдем
По формуле Пуассона искомая вероятность приближенно равна:
| ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 элементов, либо последовательно по одному элементу, причем каждый отобранный элемент исключается из исходного множества);
элементов, либо последовательно по одному элементу, причем каждый отобранный элемент исключается из исходного множества); .
. ,
, .
. и равно:
и равно: .
. Причем они отличаются друг от друга только порядком расположения букв.
Причем они отличаются друг от друга только порядком расположения букв. 30! = 265 252859 812191058636308 480 000000.
30! = 265 252859 812191058636308 480 000000.
 ,
, . Число размещений можно вычислить по формулам:
. Число размещений можно вычислить по формулам: .
.

 .
. и находятся по формуле:
и находятся по формуле: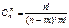 .
.
 ,
,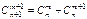 ,
, .
.
 ; б)
; б)  ; в)
; в)  .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б)  .
. ; б)
; б)  .
. .
. – «промах» при одном выстреле
– «промах» при одном выстреле


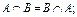












 ,
,  ,
,  ,
,  означает вероятность того, что в пяти испытаниях событие появится ровно 3 раза и, следовательно, не наступит 2 раза.
означает вероятность того, что в пяти испытаниях событие появится ровно 3 раза и, следовательно, не наступит 2 раза.
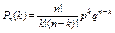 .
.
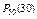 надо вычислить выражение
надо вычислить выражение 
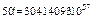 ,
, ,
,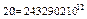 .
. того, что событие А появится в п испытаниях ровно k раз, приближенно равна (тем точнее, чем больше п) значению функции
того, что событие А появится в п испытаниях ровно k раз, приближенно равна (тем точнее, чем больше п) значению функции

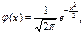 соответствующие положительным значениям аргумента х. Для отрицательных значений аргумента пользуются теми же таблицами, так как функция
соответствующие положительным значениям аргумента х. Для отрицательных значений аргумента пользуются теми же таблицами, так как функция  нечетна, т. е.
нечетна, т. е. = –
= – 
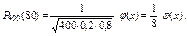



 – это функция
– это функция  действительной переменной
действительной переменной  , определяющая вероятность того, что случайная величина принимает значение меньше некоторого фиксированного числа
, определяющая вероятность того, что случайная величина принимает значение меньше некоторого фиксированного числа  :
:
 – плотность распределения вероятностей.
– плотность распределения вероятностей. , примыкающей к точке
, примыкающей к точке  .
.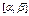 равна определенному интегралу от плотности распределения
равна определенному интегралу от плотности распределения 


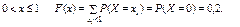




 .
.
 ,
,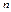 независимых испытаниях, в каждом из которых вероятность появления события равна
независимых испытаниях, в каждом из которых вероятность появления события равна  ; вероятность возможного значения
; вероятность возможного значения  (числа
(числа  появлений события) вычисляют по формуле Бернулли:
появлений события) вычисляют по формуле Бернулли: .
. определяет вероятность наступления события п – 1 раз;...; последний член qп определяет вероятность того, что событие не появится ни разу.
определяет вероятность наступления события п – 1 раз;...; последний член qп определяет вероятность того, что событие не появится ни разу.

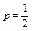 , следовательно, вероятность непоявления «герба»
, следовательно, вероятность непоявления «герба» 



 ,
, – среднее число появлений событий в
– среднее число появлений событий в  в
в 

 , зная k и
, зная k и  (Приложение 2).
(Приложение 2).