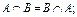Под опытом, или экспериментом, или испытанием будем понимать осуществление конкретного комплекса условий.

Опыт называется случайным, если его результат нельзя точно предсказать до его осуществления.

Пример 2.1. Подбрасывание монеты;

Процесс изготовления какой-либо детали.

Всякий результат опыта называется событием.

Событие называется случайным, если при одних и тех же условиях оно может как произойти, так и не произойти. Вместо "произойти" говорят также "наступить", "появиться", "иметь место".

Случайные события обозначаются большими буквами латинского алфавита А, В, С, …

Пример 2.2. Событие А – «попадание в мишень при стрельбе»,

событие В – «появление герба при бросании монеты».

событие С – «при подбрасывании игрального кубика выпадет 6 очков».

В приведенном определении неявно подразумевается одно важное требование, которое необходимо подчеркнуть: мы должны иметь возможность неоднократно воспроизводить одни и те же условия, в которых наблюдается данное событие (например, подбрасывать кубик), — иначе невозможно судить о его случайности. Стало быть, говоря о любом случайном событии, мы всегда имеем в виду наличие определенных условий, без которых об этом событии вообще не имеет смысла говорить. До эксперимента, как правило, невозможно точно сказать, произойдет данное событие или не произойдет — это выясняется лишь после его завершения.

 

Виды случайных событий

События,которые никогда не могут произойти называется невозможными.

События, которые происходят при каждом экспериментеназываются достоверны ми.

Пример 2.3. Событие А - «на игральном кубике выпадет 7 очков» — невозможное, а событие В – «на игральном кубике выпадет меньше семи очков» — достоверное. Разумеется, если речь идет о кубике, на гранях которого написаны числа от 1 до 6.

Два события называются несовместными, если они не могут произойти вместе при одном и том же испытании. В противном случае события называются совместными.

Пример 2.4. Несовместными являются попадание и промах при одном выстреле.

Два события называются противоположными, если появление одного из них равносильно непоявлению другого.

Если одно из противоположных событий обозначено буквой А, то другое обозначают .

Пример 2.5. Если событие А – «попадание», то событие – «промах» при одном выстреле

мишени.

Несколько событий в условиях данного опыта образуют полную группу событий, если в результате опыта произойдет обязательно хотя бы одно из них.

Пример 2.6. Учащемуся на экзамене достался билет с двумя теоретическими вопросами.

События А₁ – «учащийся знает оба вопроса»,

А₂ – «учащийся знает первый вопрос, но не знает второго»,

А₃ – «учащийся знает второй вопрос, но не знает первого»,

А₄ – «учащийся знает только один вопрос»,

А₅ – «учащийся не знает ни одного вопроса» образуют полную систему событий, среди которых имеются как несовместные А₁ и А₂, А₁ и А₅ и другие, так и совместные А₂ и А₄, А₃ и А₄.

Различают события элементарные и составные.

Так, в примере 2.6 событие А₄ является составным событием из А₂ и А₃, поэтому событие А₄ наступит только в результате наступления либо только элементарного события А₂, либо только элементарного события А₃. В таком случае говорят, что событие А₄ разлагается на элементарные события А₂ и А₃, и пишут А₄ = {А₂, А₃}.

События называются равновозможными, если условия испытания обеспечивают одинаковую возможность осуществления каждого из них.

Пример 2.7. При подбрасывании монеты событие А – «появление орла» и событие В – «появление решки» равновозможны, так как предполагается, что монета изготовлена из однородного материала, имеет правильную цилиндрическую форму и наличие чеканки не влияет на то, какая сторона монеты окажется верхней.

Каждое событие, которое может наступить в итоге опыта, называются элементарным исходом (элементарным событием, шансом).

Пример 2.8. События А_i (i = 1, 2, 3, 4, 5, 6) – «верхней гранью, появляющейся при подбрасывании игрального кубика, оказалась грань с цифрой i» – элементарные исходы.

Элементарные исходы, при которых данное событие наступает, называются благоприпятсвующими этому событию, или благоприятными.

Пример 2.9. При подбрасывании игрального кубика элементарные исходы А₂, А₄, А₆ являются благоприятными для события «выбыло четное число».

 

Операции над событиями

Дадим определения действий, которые можно производить над событиями.

Если при всяком испытании, при котором происходит событие А, происходит и событие B, то событие А называется частным случаем события B.

Говорят также, что А влечет за собой B и пишут:

А Ì B или B É A.

Пример 2.10. При бросании игральной кости событие А, состоящее в появлении двух очков, есть частный случай события B, состоящего в появлении четного числа очков.

Если А влечет за собой B, а B влечет за собой А, то эти события равносильны, так как они вместе наступают или вместе не наступают.

Суммой двух событий A и B называется событие A+B (AÈB), состоящее из элементарных событий, принадлежащих хотя бы одному из событий A или B.

Пример 2.11. Суммой событий А – «появление одного очка при бросании игральной кости» и события В – «появление двух очков при бросании игральной кости» является событие А + В – «появление не больше двух очков при бросании игральной кости»

Произведением двух событий A и B называется событие AB (AÇB), состоящих из элементарных событий, принадлежащих одновременно A и B.

Пример 2.12. Если событие А – «деталь годная», событие В – «деталь окрашенная», то событие АВ – «деталь годна и окрашена».

Разностью двух событий A и B называют событие A\B, состоящее из элементарных событий, которые входят в событие B.

Операции над событиями подчинены следующим правилам:

1.	2.
3.	4.
5.	6.
7.	8.
9.	10.
11.	12.
13.	14.
15.	16.