
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предмет математической статистикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Математическая статистика — это раздел математики, посвященный методам сбора, анализа и обработки статистических данных для научных и практических целей. Математическая статистка является разделом математики, непосредственно примыкающим к теории вероятностей. В ней рассматриваются приближенные методы нахождения законов и числовых характеристик случайной величины по результатам экспериментов или наблюдений. Статистические данные представляют собой данные, полученные в результате обследования большого числа объектов или явлений (то есть, математическая статистика имеет дело с массовыми явлениями). Математическая статистика подразделяется на две обширные области: описательная статистика – методы описания статистических данных, представления их в форме таблиц, распределений и т.п.; аналитическая статистика – обработка данных, полученных в ходе эксперимента, и формулировка выводов, имеющих прикладное значение для конкретной области человеческой деятельности. З адача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов. Современную математическую статистику определяют как науку о принятии решений в условиях неопределенности. Трудно найти современную область научных исследований, где бы ни использовались методы математической статистики. В последнее время они нашли широкое применение в медицине, биологии, социологии и других науках. Первичная обработка выборок. Генеральная совокупность и выборка Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты. Пример 7.1. Если имеется партия деталей, то качественным признаком может служить стандартность детали, а количественным – контролируемый размер детали. Иногда проводят сплошное обследование, т. е. обследуют каждый из объектов совокупности относительно признака, которым интересуются. На практике, однако, сплошное обследование применяют сравнительно редко. Так как, если совокупность содержит очень большое число объектов, то провести сплошное обследование физически невозможно. Если обследование объекта связано с его уничтожением или требует больших материальных затрат, то проводить сплошное обследование практически не имеет смысла. В таких случаях случайно отбирают из всей совокупности ограниченное число объектов и подвергают их изучению. Вся подлежащая изучению совокупность объектов наблюдений называют генеральной совокупностью. Она может состоять из конечного или бесконечного множества значений, называемых элементами генеральной совокупности. Та часть объектов, которая отобрана для непосредственного изучения из генеральной совокупности, называется выборочной совокупностью или выборкой. Число объектов в генеральной или в выборочной совокупности называют их объемом. Принято обозначать: N - объем генеральной совокупности, Пример 7.2. Если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N = 1000, а объем выборки п = 100. Основные виды выборок При составлении выборки можно поступать двумя способами: после того как объект отобран и над ним произведено наблюдение, он может быть возвращен либо не возвращен в генеральную совокупность. В соответствии со сказанным выборки подразделяют на повторные и бесповторные. Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность. Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается. На практике обычно пользуются бесповторным случайным отбором. Для того чтобы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли. Другими словами, выборка должна правильно представлять пропорции генеральной совокупности, эго требование коротко формулируют так: выборка должна быть репрезентативной (представительной). Выборка будет репрезентативной, если ее осуществить случайно: каждый объект выборки отобран случайно из генеральной совокупности, если все объекты имеют одинаковую вероятность попасть в выборку. Способы отбора На практике применяются различные способы отбора. Принципиально эти способы можно подразделить на два вида: 1. Отбор, не требующий расчленения генеральной совокупности на части. Сюда относятся: а) простой случайный бесповторный отбор (объекты извлекают по одному из всей генеральной совокупности); б) простой случайный повторный отбор. 2. Отбор, при котором генеральная совокупность разбивается на части. Сюда относятся: а) типический отбор (объекты отбираются не из всей генеральной совокупности, а из каждой ее «типической» части. Например, если детали изготовляют на нескольких станках, то отбор производят не из всей совокупности деталей, произведенных всеми станками, а из продукции каждого станка в отдельности.); б) механический отбор (генеральную совокупность «механически» делят на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект. Например, если нужно отобрать 20% изготовленных станком деталей, то отбирают каждую пятую деталь; если требуется отобрать 5% деталей, то отбирают каждую двадцатую деталь, и т. д.); в) серийный отбор (объекты отбирают из генеральной совокупности не по одному, а «сериями», которые подвергаются сплошному обследованию. Например, если изделия изготовляются большой группой станков-автоматов, то подвергают сплошному обследованию продукцию только нескольких станков.
Вариационный ряд Основная форма представления выборочной совокупности – вариационные ряды. Пусть посредством независимых испытаний, проведенных в одинаковых условиях, получены числовые значения х1, х2,..., хп. Располагают эти значения в порядке возрастания Число, показывающее, сколько раз встречается в выборке вариант Отношение числа вариантов к объему выборки (или общему числу наблюдений)
Вариационный ряд показывает, каким образом варианты связаны с их частотами в выборке. Вариационные ряды бывают двух типов: интервальные и безынтервальными. В интервальном вариационном ряду частоты характеризующие повторяемость вариант в выборке, распределяются по интервалам группировки. Интервальный вариационный ряд строится, если изучаемый признак варьирует непрерывно, но используется и для дискретно варьирующих признаков в тех случаях, когда признак варьирует в широких пределах. Пример 7.3.
В безынтервальном вариационном ряду частоты распределяются непосредственно по значениям варьирующего признака. Для построения безынтервального вариационного ряда необходимо варианты выборки расположить в порядке возрастания или убывания (проранжировать) и затем подсчитать, сколько раз каждая из них встречается в выборке. Безынтервальный вариационный ряд применяется в тех случаях, когда исследуемый признак варьирует дискретно и слабо. Пример 7.4.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 656; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.242.169 (0.006 с.) |

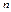 – объем выборки.
– объем выборки. и называют полученную последовательность вариационным рядом, а сами значения
и называют полученную последовательность вариационным рядом, а сами значения 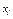 – вариантами.
– вариантами. , причем
, причем  (k – количество различных вариант).
(k – количество различных вариант).




