Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическая статистика. Ее виды, особенности, задачи.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ЯГМА Кафедра медицинской физики Лечебный факультет Курс Семестр «Элементы математической статистики» Составил: Дигурова И.И. Г. Математическая статистика. Ее виды, особенности, задачи. Математическая статистика – раздел математики, посвященный математическим методам обработки, систематизации и использования статичных данных для практических и научных целей. Задачей этого раздела является разработка практических методов, регистрации, описания, анализ экспериментальных данных, получаемых в опытах с массовыми явлениями. Особенностью статистики является изучение массовых, случайных явлений в условной неопределенности. Достоверность выводов зависит от числа объектов исследования. На основе анализов и прогнозов вырабатывается оптимальное решение. Статистика подразделяется на: - теоретическую (вырабатывает методы) прикладную (общая, отраслевая (экономическая статистика, метеорологическая, медицинская))
Медицинская статистика: - ст. рождаемости - ст. заболеваемости - ст. смертности - ст. медицинских учреждений
Биологическая статистика (=биометрия) – включает статистические методы, используемые в различных биологических исследованиях (в цистологии, микробиологии).
Статистика: - описательная (комплекс методов сбора, группировки данных и представления их в виде таблиц, графиков…) - аналитическая (делает заключения, выводы с целью практического применения)
Основные понятия описательной статистики. Их характеристика
1. Генеральная совокупность – подлежащая изучению совокупность однородных элементов, которая характеризуется некоторым признаком. Например, нас интересует распространенность данного заболевания в определенном регионе, тогда генеральная совокупность, это все население региона. Если необходимо выразить мужчин и женщин отдельно по этому заболеванию, то получаем 2 генеральные совокупности. Количество объектов, входящих в генеральную совокупность называется объемом генеральной совокупности (N) Генеральная совокупность можно изучать по некоторой ее части.
2. Выборочная совокупность - часть генеральной совокупности, выбираемая для статистической обработки (выборка) (объем выборки -n). Свойства объектов выборки должны соответствовать свойствам генеральной совокупности. Результаты исследования некоторого признака генеральной совокупности, будут более надежны, если выборку образовывать случайным образом. Элементы выборки берутся наугад. Каждый объект может попасть в выборку с одинаковой вероятностью. Главным вопросом является: как определить объем выборки, необходимой для получения необходимого результата.
3. Варианта – значение признака для каждого элемента выборки (х) Признаки могут быть качественными и количественными Количественные делятся на непрерывные (масса тела) и дискретные (количество волос)
Признак, имеющий значение от одного объекта к другому называется варьирующимся. Если количественный признак лежит в интервале – интервальный.
4. Частота – количество объектов с конкретным числовым значением признака xi 35 36 37 38 39 40 41 ni (pi): 2 4 5 6 7 7 2
5. Частность или относительная частота – доля варианта с данным значением признака (ni/n)
Основные меры положения и рассеяния.
Меры положения частного распределения, их характеристика. На практике ряды распределения описываются различными числовыми характеристиками (мерами).
1 Мода (Мо) – это варианта, наиболее часто встречающаяся в совокупности (= модальное значение).
2 Медиана (Ме) – это величина, делящая ранжированный ряд на 2 равные части. Так же она делит площадь под кривой распределения. Для того, чтобы определить Ме надо ранжировать ряд (в порядке возрастания), вычислить номер, под которым стоит медиана. N/2 – Для четных, (N+1)/2 – Для нечетного количества объектов
3 Средняя арифметическая простая – это частное деление суммы всех значений признака на их общее число объектов X=(X1+X2+X3…+Xn)/N Сумма всех <+> и <–> отклонений от х равно «0».
Среднюю арифметическую простую вычисляют для неупорядоченных рядов в тех случаях, когда каждая варианта встречается 1 раз.
4 Средняя взвешенная Если в совокупности отдельные варианты встречаются неоднократно, то вычисляется средняя взвешенная – это величина, полученная суммированием произведений числовых значений вариант на их частоты с последующим делением суммы на количество всех вариант.
5 Средняя квадратическая используется, если признаки выражаются мерами площади. Пример: размер колонии микробов, листовых пластинок.
Его характеристика.
Разброс числовых значений вариант (генеральной, выборочной совокупности) относительно средних значений характеризуется мерами рассеяния. 1. Лимит – минимальная и максимальная варианта совокупности. (Xmin, Xmax) 2. Вариационный размах – разность между максимальным и минимальным значением R=Xmax-Xmin 3. Индивидуальное отклонение – разность между числовым значением варианты и средним арифметическим всей совокупности Di=Xi- 4. Дисперсия – мера рассеяния, полученная суммированием квадратов индивидуальных отклонений и последующим делением суммы на объем совокупности.
Если число объектов менее 30, то рассчитывается исправленная дисперсия (Сигма с крышей)
Где N-1 – число степеней свободы. Это число на 1 меньше, чем весь объем свободности
5. Стандартное (среднее квадратичное) отклонение. Эта мера рассеяния, равная корню квадрата дисперсии, S=корень квадратный из
6. Коэффициент вариации - мера рассеяния равна, отношению стандартного отклонения к средней арифметической V=(S/X)100% При нормальном распределении коэффициент вариации не > 50%, а часто гораздо ниже (приблизительно 20%)
3. Выборочный метод. Выборки, их виды и требования к ним. Для того, чтобы получить исчерпывающую информацию о состоянии генеральной совокупности нужно учесть весь ее состав без исключения. Но не всегда есть возможность или необходимость прибегать к сплошному исследованию. В целях экономии времени и средств, анализу подвергается часть совокупности выборки, по ней судят о состоянии всей совокупности в целом. Если число объектов менее 30, то выборка называется малой. В зависимости от способов формирования, выборки бывают повторные – с возвратом, неповторные – без возврата
Требования к выборкам А)Рендомизация - каждая варианта генеральной совокупности имеет одинаковую вероятность для попадания в выборку. Репрезентативность – состав и структура выборки должны соответствовать составу и структуре генеральной совокупности.
ЯГМА Кафедра медицинской физики Лечебный факультет Курс Семестр «Элементы математической статистики» Составил: Дигурова И.И. Г. Математическая статистика. Ее виды, особенности, задачи. Математическая статистика – раздел математики, посвященный математическим методам обработки, систематизации и использования статичных данных для практических и научных целей. Задачей этого раздела является разработка практических методов, регистрации, описания, анализ экспериментальных данных, получаемых в опытах с массовыми явлениями. Особенностью статистики является изучение массовых, случайных явлений в условной неопределенности. Достоверность выводов зависит от числа объектов исследования. На основе анализов и прогнозов вырабатывается оптимальное решение. Статистика подразделяется на: - теоретическую (вырабатывает методы) прикладную (общая, отраслевая (экономическая статистика, метеорологическая, медицинская))
Медицинская статистика: - ст. рождаемости - ст. заболеваемости - ст. смертности - ст. медицинских учреждений
Биологическая статистика (=биометрия) – включает статистические методы, используемые в различных биологических исследованиях (в цистологии, микробиологии).
Статистика: - описательная (комплекс методов сбора, группировки данных и представления их в виде таблиц, графиков…) - аналитическая (делает заключения, выводы с целью практического применения)
Основные понятия описательной статистики. Их характеристика
1. Генеральная совокупность – подлежащая изучению совокупность однородных элементов, которая характеризуется некоторым признаком. Например, нас интересует распространенность данного заболевания в определенном регионе, тогда генеральная совокупность, это все население региона. Если необходимо выразить мужчин и женщин отдельно по этому заболеванию, то получаем 2 генеральные совокупности. Количество объектов, входящих в генеральную совокупность называется объемом генеральной совокупности (N) Генеральная совокупность можно изучать по некоторой ее части.
2. Выборочная совокупность - часть генеральной совокупности, выбираемая для статистической обработки (выборка) (объем выборки -n). Свойства объектов выборки должны соответствовать свойствам генеральной совокупности. Результаты исследования некоторого признака генеральной совокупности, будут более надежны, если выборку образовывать случайным образом. Элементы выборки берутся наугад. Каждый объект может попасть в выборку с одинаковой вероятностью. Главным вопросом является: как определить объем выборки, необходимой для получения необходимого результата.
3. Варианта – значение признака для каждого элемента выборки (х) Признаки могут быть качественными и количественными Количественные делятся на непрерывные (масса тела) и дискретные (количество волос)
Признак, имеющий значение от одного объекта к другому называется варьирующимся. Если количественный признак лежит в интервале – интервальный.
4. Частота – количество объектов с конкретным числовым значением признака xi 35 36 37 38 39 40 41 ni (pi): 2 4 5 6 7 7 2
5. Частность или относительная частота – доля варианта с данным значением признака (ni/n)
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 2133; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.135.67 (0.013 с.) |

 =(х1n1+x2n2+x(n)n(n))/N x1n1+y2n2
=(х1n1+x2n2+x(n)n(n))/N x1n1+y2n2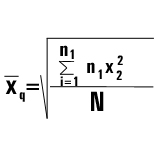

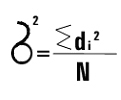
 - для генеральной
- для генеральной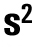 - для выборочной совокупности
- для выборочной совокупности
 . Чем сильнее варьирует признак, тем больше величина среднего квадратного отклонения.
. Чем сильнее варьирует признак, тем больше величина среднего квадратного отклонения.