
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графическое представление вариационных рядовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для повышения наглядности вариационных рядов, используется их графическое представление. Наиболее распространенными способами графического представления являются гистограмма и полигон частот. Гистограмма Гистограмма используется для графического представления распределений непрерывно варьирующих признаков и состоит из примыкающих друг к другу прямоугольников. Основание каждого прямоугольника равно ширине интервала группировки, а высота его такова, что площадь прямоугольника пропорциональна частоте (или относительной частоте) попадания в данный интервал. Если ряд безинтервальный, то ширина всех столбцов выбирается произвольной, но одинаковые. На графике гистограммы основание прямоугольников откладывается по оси x, а высота — по оси у прямоугольной системы координат. Пример 7.5.
Рис 7.1. Гистограмма количества нарушений скорости (пример 6.3.)
Рис. 7.2. Гистограмма итогов сдачи экзамена (пример 6.4.) Полигон частот Полигон частот образуется ломаной линией, соединяющей точки, соответствующие срединным значениям интервалов группировки и частотам этих интервалов, срединные значения откладываются по оси х, а частоты – по оси у. Из сравнения двух рассмотренных способов графического представления эмпирических распределений следует, что для получения полигона частот из построенной гистограммы нужно середины вершин прямоугольников, образующих гистограмму, соединить отрезками прямых. Полигончастот используется для представления распределений как непрерывных, так и дискретных признаков. В случае непрерывного распределения полигон частот является более предпочтительным способом графического представления, чем гистограмма, если график эмпирического распределения описывается плавной зависимостью. Пример 7.6.
Рис. 7.3. Полигон частот итогов сдачи экзамена (пример 6.4.) Эмпирическая функция распределения Эмпирической функцией распределения называется функция F*(х), определяющая для каждого значения х относительную частоту события X < х, т.е. по определению
где пх — количество вариант, значения которых меньше чем х; п — объем выборки. Свойства эмпирической функцией распределения: 1. При 2. При 3. При 4.
Пример 7.7. Построить эмпирическую функцию по условию примера 6.4. Решение. Найдем объем выборки: п = 1 + 4 + 3 + 3 +2 +5 + 3 + 1 + 2 + 1 = 25. Наименьшая варианта равна единице, поэтому Значение 1 < х
или
Построим график полученной функции.
Рис. 7.4 График эмпирической функции Числовые характеристики выборки Вариационные ряды и графики эмпирических распределений дают наглядное представление о том, как варьирует признак в выборочной совокупности. Но они недостаточны для полной характеристики выборки, поскольку содержат много деталей, охватить которые невозможно без применения обобщающих числовых характеристик. Числовые характеристики выборки дают количественное представление об эмпирических данных и позволяют сравнивать их между собой. Характеристики положения Чаще всего употребляются такие характеристики положения, как среднее арифметическое, медиана и мода. Среднее арифметическое Среднее арифметическое, или просто среднее, — одна из основных характеристик выборки. Среднее арифметическое – такое значение признака, сумма отклонений от которого выборочных значений признака равна нулю (с учетом знака отклонения). Среднее принято обозначать той же буквой, что и варианты выборки, с той лишь разницей, что над буквой ставится символ усреднения — черта. Например, если обозначить исследуемый признак через X, а его числовые значения — через xi, то среднее арифметическое имеет обозначение Среднее арифметическое, как и другие числовые характеристики выборки, может вычисляться как по необработанным первичным данным, так и по результатам группировки этих данных. Для несгруппированных данных среднее арифметическое определяется по следующей формуле:
где n — объем выборки; хi — варианты выборки. Если данные сгруппированы, то
где n — объем выборки; k — число интервалов группировки;
ni — частота i -ого интервала; хi — срединное значение i -ого интервала. Среднее арифметическое – величина того же наименования, что и значения признаков. Нахождение среднего арифметического непрерывного вариационного ряда осложняется, если крайние интервалы не замкнуты (то есть имеют вид «менее 10» или «более 60»). В этом случае считается, что ширина первого интервала равна ширине второго, а ширина последнего – ширине предпоследнего. Среднее арифметическое, вычисленное по формуле называют также взвешенным средним, подчеркивая этим, что в формуле xi, суммируются с коэффициентами (весами), равными частотам попадания в интервалы группировки. Медиана Медианой (Ме) называется такое значение признака X, когда ровно половина значений экспериментальных данных меньше ее, а вторая половина — больше. Если данных немного (объем выборки невелик), медиана вычисляется очень просто. Для этого выборку ранжируют, т. е. располагают данные в порядке возрастания или убывания, и в ранжированной выборке, содержащей n членов, ранг R (порядковый номер) медианы определяется как
Пример 7.8. Имеется ранжированная выборка, содержащая нечетное число членов n = 9: 12, 14, 14, 18, 20, 22, 22, 26, 28. Тогда ранг медианы:
и медиана совпадает с пятым членом ряда: Ме = 20. Если выборка содержит четное число членов, то медиана не может быть определена столь однозначно. Пример 7.9. Имеется ранжированная выборка, содержащая 10 членов: 6, 8, 10, 12, 14, 16, 18, 20, 22, 24. Ранг медианы оказывается равным:
Медианой в этом случае может быть любое число между 14 и 16 (5-м и 6-м членами ряда). Для определенности принято считать в качестве медианы среднее арифметическое этих значений, т. е.:
Если необходимо найти медиану для сгруппированных данных, то поступают следующим образом. Вначале находят интервал группировки, в котором содержится медиана, путем подсчета накопленных частот или накопленных относительных частот. Медианным будет тот интервал, в котором накопленная частота впервые окажется больше
где hme — ширина медианного интервала;
Пример 7.10. Найти медиану для интервального ряда примера 6.3.
Объем выборки равен п = 50 + 32 + 26 + 11 + 5 = 124. Найдем медианный интервал – интервал, в котором накопленная частота впервые окажется больше Так как, накопительная частота второго интервала 50 + 32 = 82 > 62, то следовательно интервал (30; 40) будет медианным и Значит,
Медиана обычно несколько отличается от среднего арифметического. Так бывает всегда, когда имеет место несимметричная форма эмпирического распределения.
Мода Мода (Мо) представляет собой значение признака, встречающееся в выборке наиболее часто. Ряд называется унимодальным, если в нем только одно модальное значение и полимодальным, если есть несколько значений признака, которые встречаются одинаково часто. Для полимодального ряда моду не вычисляют.
Для дискретного ряда мода находится по определению. Интервал группировки с наибольшей частотой называется модальным. Для определения моды в интервальном ряду используется следующая формула:
где h — ширина интервала группировки; nMo — частота модального интервала; nMo-1 — частота интервала, предшествующего модальному; nMo+1 — частота интервала, следующего за модальным. Характеристики рассеяния Средние значения не дают полной информации о варьирующем признаке. Нетрудно представить себе два эмпирических распределения, у которых средние одинаковы, но при этом у одного из них значения признака рассеяны в узком диапазоне вокруг среднего, а у другого – в широком. Поэтому наряду со средними значениями вычисляют и характеристики рассеяния выборки. Рассмотрим наиболее употребительные из них. Размах вариации Размах вариации – разность между максимальной и минимальной вариантами выборки:
Как видим, размах вычисляется очень просто, и в этом его главное и единственное достоинство. Информативность этого показателя невелика. Можно привести очень много распределений, сильно отличающихся по форме, но имеющих одинаковый размах. Размах вариации используется иногда в практических исследованиях при малых (не более 10) объемах выборки, Например, по размаху вариации легко оценить, насколько различаются лучший и худший результаты в группе спортсменов. При больших объемах выборки к его использованию надо откоситься с осторожностью.
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 2277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.218.118 (0.009 с.) |




 ,
,
 ;
;
 ;
;
 ;
; – функция неубывающая.
– функция неубывающая. 2, наблюдалось 1 раз, следовательно,
2, наблюдалось 1 раз, следовательно,  .
.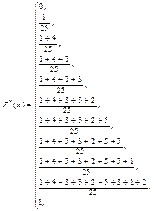
 2;
при 2 < х
2;
при 2 < х 

 .
.





 или накопленная относительная частота — больше 0,5. Внутри медианного интервала медиана определяется по следующей формуле:
или накопленная относительная частота — больше 0,5. Внутри медианного интервала медиана определяется по следующей формуле: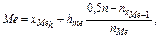
 — нижняя граница медианного интервала;
— нижняя граница медианного интервала; — накопленная частота интервала, предшествующего медианному,
— накопленная частота интервала, предшествующего медианному, — частота медианного интервала.
— частота медианного интервала.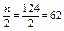 или накопленная относительная частота — больше 0,5.
или накопленная относительная частота — больше 0,5.

 — нижняя граница модального интервала;
— нижняя граница модального интервала; .
.


