
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды и формы представления системных структур.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Структура системы может быть представлена в символической (математической) форме – с помощью теоретико-множе-ственных описаний, языка топологии, алгебры и других символических средств представления (моделирования) структуры систем, но чаще всего используют наиболее наглядную графическую форму представления системных структур – в виде плоского графа сетевой, иерархической или матричной формы (рис.4). Разновидностями многоуровневых иерархических структур считают: стратифицированные, слоистые, эшелонированные и смешанные иерархические структуры. Сетевая структура или сеть представляет собой декомпозицию системы во времени (рис. 4 а)). Такие структуры могут отображать порядок действия технической системы (телефонная сеть, электрическая сеть и т. п.), этапы деятельности человека (при производстве продукции - сетевой график, при проектировании - сетевая модель, при планировании - сетевой план и т. д.). В виде сетевых моделей могут представляться и методики системного анализа. Иерархические структуры представляют собой декомпозицию системы в пространстве (рис. 4 б - д). Все компоненты (вершины, узлы) и связи (дуги, соединения узлов) существуют в этих структурах одновременно (не разнесены во времени). Такие структуры могут иметь не два (как для простоты показано на рис. 2 б и в), а большее число уровней декомпозиции (структуризации). Структуры, показанные на рис. 4 б называют древовидными структурами (структурами типа «дерево») или иерархическими структурами с «сильными» связями.Каждый элемент нижележащего уровня в таких структурах подчинен одному узлу (одной вершине) вышестоящего уровня. Структуры, показанные на рис. 4 в, в которых элемент нижележащего уровня может быть подчинен двум и более узлам (вершинам) вышестоящего уровня, называют иерархическими структурами со «слабыми» связями. Матричные структуры. Иерархическим структурам, приведенным на рис. 4 б и 4 в, соответствую матричные структуры рис. 4 е, 4 ж. Отношения, имеющие вид «слабых» связей между двумя уровнями на рис. 4 в, подобны отношениям в матрице, образованной из составляющих этих двух уровней на рис. 4 ж. В форме матричного представления могут быть представлены взаимоотношения между уровнями иерархической структуры. Например, древовидная иерархическая структура, приведенная на рис. 4 б, может быть представлена матричной структурой, приведенной на рис. 4 e, что иногда удобнее на практике при оформлении планов, поскольку помимо иерархической соподчиненности тематической основы плана, в нем нужно еще указать исполнителей, сроки выполнения, формы отчетности и др. сведения, необходимые для контроля выполнения плана. Разновидностью такого вида матричного представления иерархических взаимоотношений используется в толковых словарях, в информационно-поисковых языках дескрипторного типа, в автоматизированных диалоговых процедурах анализа целей и функций, поскольку при использовании таких диалоговых процедур первоначально не известно количество ветвей на каждом уровне иерархии. В виде двумерной матричной структуры (рис. 4 ж) могут быть представлены взаимоотношения между уровнями иерархии со "слабыми" связями (рис. 4 в); при этом помимо наличия связей в матрице может быть охарактеризована и сила связей либо словами ("сильная" (+), "слабая" (‑)), либо путем введения количественных характеристик силы (значимости, длительности и т. п.) связи. Матричные структуры могут быть и многомерными. Но в этих случаях графическое их представление становится неудобным, и тогда применяют символическое алгебраическое представление, представление многомерной структуры в виде так называемого тензора.
Кроме того, матричные структуры сложных систем могут быть представлены и в форме, когда одна или даже все оси структуры образованы как иерархические, что, например, имеет место при представлении организационных структур, сочетающих линейный, функциональный и программно-целевой принципы управления Многоуровневые иерархические структуры. На рис. 4 г показаны смешанные иерархические структуры‑ с вертикальными и горизонтальными связями, которые использовались, например, в общегосударственной автоматизированной системе управления (ОГАС) СССР (рис. 5).
Горизонтальные взаимодействия устанавливались между общегосударственными органами управления при принятии решений по сложным проблемам для согласования решений и взаимного обмена информацией. В теории систем М. Месаровича предложены особые классы многоуровневых иерархических структур, отличающиеся различными принципами взаимоотношений элементов в пределах уровня и различным правом вмешательства вышестоящего уровня в организацию взаимоотношений между элементами нижележащего, для названия которых он предложил следующие термины: «страты», «слои», «эшелоны» (рис. 4 д). Страты. Это специальный класс многоуровневых иерархических структур, позволяющий представлять сложные системы семействомиерархических моделей, каждая из которых описывает поведение системы с точки зрения соответствующего уровня абстрагирования. Для каждого уровня существуют характерные особенности, законы и принципы, с помощью которых описывается поведение системы на этом уровне. Такое представление названо стратифицированным, а уровни абстрагирования - стратами [1]. Стратифицированное представление может использоваться и как средство последовательного углубления представления о системе, ее детализации (рис. 6): чем ниже опускаемся по иерархии страт, тем более детальной становится модель системы; чем выше поднимаемся, тем яснее становится смысл и значение всей системы.
Рис. 6. Страты детализации системы Объяснить назначение системы с помощью элементов нижней страты в сложных системах практически невозможно. Аналогичное представление используется при разработке банков и баз данных, в которых принято выделять физический уровень хранения данных, логический или концептуальный уровень и внешний или системно-логический уровень. Примером стратифицированного описания может также служить предложенное Ю.И.Черняком выделение уровней абстрагирования системы - от философского или теоретико-познавательного описания ее замысла до материального воплощения (рис. 7).
Рис. 7. Страты разных уровней абстрагирования системы Такое представление помогает понять, что одну и ту же систему на разных стадиях познания и проектирования можно (и нужно) описывать различными выразительными средствами, т.е. как бы на разных «языках»: философском или теоретико-познавательном – в виде вербального описания замысла, концепции; представление системы на научно-исследовательском языке – в форме моделей разного рода, помогающих глубже понять и раскрыть замысел системы; проектном – в форме технического задания и технического проекта, для разработки и представления которого могут понадобиться математические расчеты, принципиальные схемы; конструкторском – в форме конструкторских чертежей, сопровождающей их документации; технологическом – в виде технологических карт, стандартов и технологической документации; материальное воплощение (реализация) системы – в форме деталей, блоков, собранного изделия или созданной системы, принципы функционирования которой отражены в соответствующей документации (инструкциях, положениях и т. п.). Слои. Второй вид многоуровневых структур предложен М.Месаровичем для организации процессов принятия решений. Для уменьшения неопределенности ситуации выделяются уровни сложности принимаемого решения - слои, т. е. определяется совокупность последовательно решаемых проблем. При этом выделение проблем осуществляется таким образом, чтобы решение вышележащей проблемы определяло бы ограничения (допустимую степень упрощения) при моделировании на нижележащем уровне, т. е. снижало бы неопределенность нижележащей проблемы, но без утраты замысла решения общей проблемы. Многослойная иерархия проиллюстрирована на рис. 8, где каждый слой представляет собой блок Di, принимающий решения и вырабатывающий ограничения Xi- 1, для нижележащего (i - 1)-го блока. «Слои» (уровни сложности) - вид многоуровневых структур, предложенный Михаилом Месаровичем для организации процессов принятия решений. Слои или уровни сложности принимаемого решения выделяются для уменьшения неопределенности ситуации. Иными словами, определяется совокупность последовательно решаемых проблем. При этом выделение проблем осуществляется таким образом, чтобы решение вышележащей проблемы определяло бы ограничения (допустимую степень упрощения) при моделировании на нижележащем уровне, т.е. снижало бы неопределенность нижележащей проблемы, но без утраты замысла решения общей проблемы.
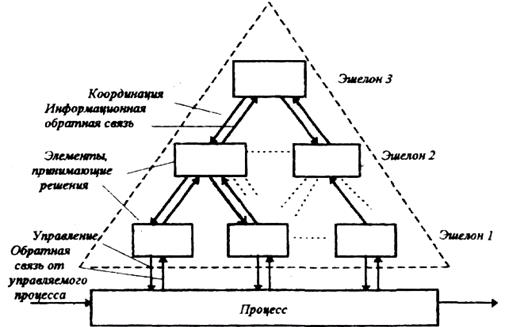
(а) (б) Рис. 8. Многослойная система принятия решений Многослойные системы принятия решений полезно формировать для решения задач планирования и управления промышленными предприятиями, отраслями, народным хозяйством в целом. При постановке и решении таких проблем нельзя раз и навсегда определить цели, выбрать конкретные действия, так как экономические и технологические условия производства непрерывно изменяются. Все это можно отразить в многослойной модели принятия решений. Эшелоны. Понятие многоэшелонной иерархической структуры вводится следующим образом: система представляется в виде относительно независимых, взаимодействующих между собой подсистем. При этом некоторые (или все) подсистемы имеют права принятия решений, а иерархическое расположение подсистем (многоэшелонная структура) определяется тем, что некоторые из них находятся под влиянием или управляются вышестоящими системами. Структурные представления такого типа условно проиллюстрированы на рис. 4 д и, более детально, ‑ на рис. 9. Уровень такой иерархии называют эшелоном. Основной отличительной особенностью многоэшелонной структуры является предоставление подсистемам всех уровней определенной свободы в выборе их собственных решений; причем эти решения могут быть (но не обязательно) не теми решениями, которые бы выбрал вышестоящий уровень. Можно показать, что предоставление свободы действий в принятии решений компонентам всех эшелонов иерархической структуры повышает эффективность ее функционирования. Кроме того, подсистемам предоставляется определенная свобода и в выборе целей. Поэтому многоэшелонные структуры называют также многоцелевыми. В таких системах могут быть использованы разные способы принятия решений. Естественно, что при предоставлении прав самостоятельности в принятии решений подсистемы могут формировать противоречащие друг другу ("конфликтные") цели и решения, что затрудняет управление, но является в то же время одним из условий повышения эффективности функционирования системы. Разрешение конфликтов достигается путем вмешательства вышестоящего эшелона. Управляющие воздействия для разрешения этих противоречий со стороны вышестоящих уровней иерархии могут быть разной силы.
Рис. 9. Эшелонированная иерархия с координационными и Для того, чтобы на это обратить внимание предлагается разделять понятия собственно "управления" и "координации". При этом последняя может иметь разную силу воздействия ("'вмешательства") и осуществляется в разной форме. В связи с этим теорию многоуровневых систем М. Месаровича иногда называют теорией координации. В этой теории рекомендуется, чтобы в процессе принятия решений подсистемы не всегда стремились бы отстаивать свои интересы, доводя дело до конфликтных ситуаций, а вступали бы в коалиции. В зависимости от принятых принципов (конфликты или коалиции), силы и форм вмешательства вышестоящих эшелонов в дела нижележащих, процесс принятия решения может происходить по-разному, т. е. по-разному может быть организована система управления принятием решений, поэтому многоэшелонные, многоцелевые иерархические структуры называют также организационной иерархией. Отношения, подобные принятым в эшелонированных структурах, реализуются в практике управления в форме так называемых холдинговых структур или холдингов. Правила взаимоотношений между фирмами, банками, торговыми домами и другими организациями, входящими в холдинг, оговариваются в соответствующих договорах и других нормативно-правовых и нормативно-технических документах. Жизненным циклом (ЖЦ) системы называют период времени от формирования концепции системы до её ликвидации («смерти»). В центре этого процесса оказываются этапы создания (рождения) и функционирования системы. В процессе функционирования системы возможны периоды становления (созревания), роста (развития) и снижения (деградации) эффективности (рис. 10).
Рис. 10. Процессы жизненного цикла систем 1.2.3. Понятия, связанные с функционированием и С понятием жизненного цикла связаны понятия «функционирование» и «развитие» системы. Понятие «состояние». Фукционирование системы обычно связывают с процессами[2], протекающими в системе и изменяющими некоторые из её характеристик, называемых состояниями, иобозначаемых как si, i= 1, 2, … k (где символ s происходит от англ. state – состояние). Состояния системы определяют либо через выходные результаты базовых (например, производственных) процессов, протекающих в системе, либо через макропараметры, макросвойства системы (например, давление, скорость, ускорение, производительность производственных процессов и т.д.). Системы, не меняющие своё состояние, называют статическими. О таких системах говорят, что они находятся в состоянии покоя (стабильные входные воздействия и выходные сигналы, не меняющиеся во времени характеристики, связанные с состоянием системы, т.е. функция s не зависит от времени). В динамических системах состояние становится функцией времени s (t), т.е. параметры состояния начинают изменяться во времени, становясь процессами, которые определяют динамику поведения системы. С понятием состояния в теории систем связаны такие понятия как ситуация, проблема и поведение. Ситуацией – называют совокупность состояний системы и среды в один и тот же момент времени. Проблема – это несоответствие между существующим (текущим) и требуемым (целевым) состоянием системы при данном состоянии среды в рассматриваемый момент времени (sтек ¹ sцел). Поведение. Если система способна переходить из одного состояния в другое (например, s 1 ,® s 2® s 3®...), то говорят, что она обладает поведением. Заметим, что изменчивость состояния во времени характерна для динамических систем, когда состояние есть функция временного аргумента s (t). При этом, если состояние меняется скачками в отдельные моменты времени (рис. 11 а), то систему называют дискретной. Если же состояния изменяются непрерывно, то система называется непрерывной (рис. 11 б). Существуют и смешанные дискретно-непрерывные системы, состояния которых меняется то скачками, то – непрерывно.
а б Рис. 11. Функция состояния непрарывных (а) и Рассматривая элементы ai самого общего определения системы (S = <A, R>) как «чёрные ящики» (поскольку они считаются неделимыми на более мелкие компоненты) с управляющими (y (t)) и возмущающими (неконтролируемыми) входами (x (t)) и выходом g (t) = f (a (t), y (t), x (t)) (рис. 12), то в зависимости от задачи состояние элемента а может быть определено как { а (t), y (t)}, { а (t), y (t), g (t)}или { а (t), y (t), х (t), g (t)}.
x (t) y (t) g (t) Рис. 12. Абстрактная модель элемента a некоторой системы С учетом введенных обозначений поведение системы можно представить как функцию состояния, определяемую состоянием в предшествующий момент времени: s (t) = [ s (t - 1), y (t), x (t)]
Устойчивость. Под устойчивостью понимают способность системы возвращаться в состояние равновесия после того, как она была из этого состояния выведена под влиянием внешних (или в системах с активными элементами - внутренних) возмущающих воздействий. Эта способность обычно присуща системам при постоянном у (t)только тогда, когда отклонения не превышают некоторого предела.
Равновесие и устойчивость в экономических системах, несмотря на кажущуюся аналогию с техническими, - гораздо более сложные понятия, и ими можно пользоваться в основном как некоторыми аналогиями для предварительного описания поведения системы. Развитие – это процесс совершенствования, улучшения параметров, функций и поведения (деятельности) динамических систем. Это понятие помогает объяснить сложные термодинамические и информационные процессы в природе и обществе. Исследование процесса развития, соотношения развития и устойчивости, изучение механизмов, лежащих в их основе, - наиболее сложные задачи теории систем. Существует особый класс развивающихся (самоорганизующихся) систем, обладающих особыми свойствами и требующих использования специальных подходов к их моделированию.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 1818; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.71.146 (0.016 с.) |


 Рис. 5. Структура системы государственного управления СССР
Рис. 5. Структура системы государственного управления СССР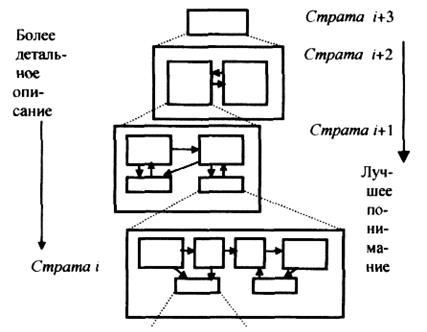





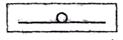 Равновесие. Понятие равновесие определяют как способность системы в отсутствии внешних возмущающих воздействий (или при постоянных воздействиях) сохранять свое состояние сколь угодно долго. Это состояние называют состоянием равновесия.
Равновесие. Понятие равновесие определяют как способность системы в отсутствии внешних возмущающих воздействий (или при постоянных воздействиях) сохранять свое состояние сколь угодно долго. Это состояние называют состоянием равновесия.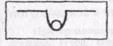 Состояние равновесия, в которое система способна возвращаться, называют устойчивым состоянием равновесия. Возврат в это состояние может сопровождаться колебательным процессом. Соответственно в сложных системах возможны неустойчивые состояния равновесия.
Состояние равновесия, в которое система способна возвращаться, называют устойчивым состоянием равновесия. Возврат в это состояние может сопровождаться колебательным процессом. Соответственно в сложных системах возможны неустойчивые состояния равновесия. В самоорганизующихся, развивающихся системах говорят о динамическом равновесии, и устойчивость можно условно представить состоянием равновесия как бы "на ступеньке" (рис. 16). Внешнее воздействие может либо вывести систему на более высокий уровень, либо "столкнуть" ее на более низкий.
В самоорганизующихся, развивающихся системах говорят о динамическом равновесии, и устойчивость можно условно представить состоянием равновесия как бы "на ступеньке" (рис. 16). Внешнее воздействие может либо вывести систему на более высокий уровень, либо "столкнуть" ее на более низкий.


