Показатели эффективности и качества систем

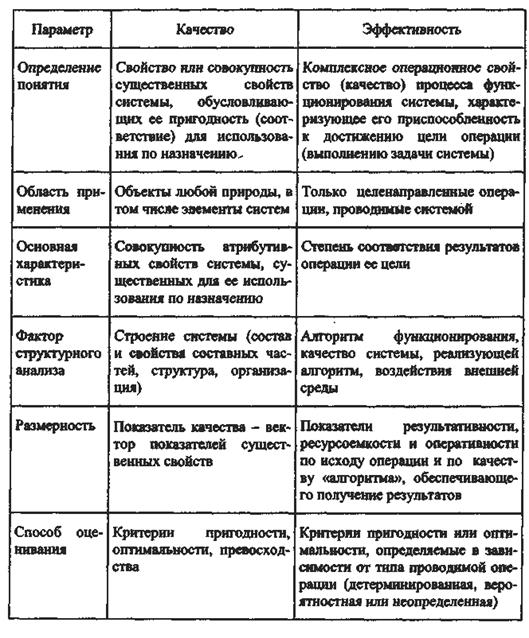
Искусственные системы создаются, как правило, для реализации одной или ряда операций. Требуемый и реально достигаемый системой результаты могут различаться. Это зависит от условий протекания операции, качества системы, реализующей операцию, и способов достижения требуемых результатов. Поэтому при оценке систем принято различать качество систем и эффективность реализуемых системами процессов.

Эффективность относят не к самой системе, а к выполняемой ею операции. Эффективность, как группа свойств, представляет только качество функционирования системы соответствие требуемого и достигаемого результата.

Соотношение понятий качества и эффективности представлено в табл. 3.1.

Для рассмотрения утверждений, приведенных в табл. 3, введем ряд понятий.

Каждое i -e качество j -й системы, i = 1,..., n; j = 1,..., m, может быть описано с помощью некоторой выходной переменной y^j_i отображающей определенное существенное свойство системы, значение которой характеризует меру (интенсивность) этого качества. Эту меру назовем показателем свойства или частным показателем качества системы. Показатель y^j_i может принимать значения из множества (области) допустимых значений { у ^доп _i }.

Назовем обобщенным показателем качества j -й системы вектор Y^j = < у^j ₁, у^j ₂,..., y^j_i,..., y^j_n >, компоненты которого суть показатели его отдельных свойств. Размерность этого вектора определяется числом существенных свойств системы. Обратим внимание на то, что показатель качества именно вектор, а не простое множество частных показателей, поскольку между отдельными свойствами могут существовать связи, которые в рамках теории множеств описать весьма сложно.

Таблица 3.1. Соотношение понятий качества и эффективности

 

 

Частные показатели имеют различную физическую природу и в соответствии с этим различную размерность. Поэтому при образовании обобщенного показателя качества следует оперировать не с «натуральными» показателями, а с их нормированными значениями, обеспечивающими приведение показателей к одному масштабу, что необходимо для их сопоставления.

Задача нормировки решается, как правило, введением относительных безразмерных показателей, представляющих собой отношение «натурального» частного показателя к некоторой нормирующей величине, измеряемой в тех же единицах, что и сам показатель

где у_i ⁰ - некоторое «идеальное» значение i -го показателя.

Выбор нормирующего делителя для перевода частных показателей в безразмерную форму в значительной мере носит субъективный характер и должен обосновываться в каждом конкретном случае.

Возможны несколько подходов к выбору нормирующего делителя.

Во-первых, нормирующий делитель у_i ⁰ можно задавать с помощью ЛПР, и это предполагает, что значение у_i ⁰ является образцовым.

Во-вторых, можно принять, что нормирующий делитель у_i ⁰= max у^j_i.

В-третьих, в качестве нормирующего делителя может быть выбрана разность между максимальными и минимальными допустимыми значениями частного показателя.

Требуемое качество системы задается правилами (условиями), которым должны удовлетворять показатели существенных свойств, а проверка их выполнения называется оцениванием качества системы. Таким образом, критерий качества это показатель существенных свойств системы и правило его оценивания.

Назовем идеальной системой Y * гипотетическую модель исследуемой системы, идеально соответствующую всем критериям качества, вектор Y* = < y *₁, y *₂, …, y^j_i, …, y * _n >, являющийся показателем качества идеальной системы.

Назовем областью адекватности некоторую окрестность значений показателей существенных свойств. В общем виде область адекватности определяется как модуль нормированной разности между показателем качества Y ^доп и показателем качества Y *:

где d - радиус области адекватности.

На радиус области адекватности накладываются ограничения, зависящие от семантики предметной области. Как правило, определение этой величины является результатом фундаментальных научных исследований или экспертной оценки.

При таком рассмотрении все критерии в общем случае могут принадлежать к одному из трех классов:

1. Критерий пригодности К ^приг:

i= 1,…, n

правило, согласно которому j -я система считается пригодной, если значения всех i -х частных показателей y^j_i,- этой системы принадлежат области адекватности d, а радиус области адекватности соответствует допустимым значениям всех частных показателей.

2. Критерий оптимальности K ^опт:

правило, согласно которому j -я система считается оптимальной по i -му показателю качества, если существует хотя бы один частный показатель качества y^j_i, значение которого принадлежит области адекватности d, а радиус области адекватности по этому показателю оптимален. Оптимальность радиуса адекватности определяется из семантики предметной области, как правило, в виде d^опт = 0, что подразумевает отсутствие отклонений показателей качества от идеальных значений.

3. Критерий превосходства К ^прев:

(" i) (y^j_i Îd½d i ®d^опт, i = 1,..., n)

правило, согласно которому j -я система считается превосходной, если все значения частных показателей качества y^j_i, принадлежат области адекватности d, а радиус области адекватности оптимален по всем показателям.

Иллюстрация приведенных формулировок приведена на рис. 39 где по свойствам y _l и у ₂ сравниваются характеристики пяти систем { Y ¹, Y ², Y ³, Y ⁴, Y ⁵}, имеющие допустимые области адекватности значений { у ^/ _i, y^//_i }, i = 1,2, для которых определены оптимальные значения у ^опт₁, y ^опт₂ соответственно.

Из рис. 39 видно, что системы Y ¹, Y ², Y ³, Y ⁵ пригодны по свойствам у ₁, и у ₂. Системы Y ¹ и Y ³ оптимальны по свойству у ₁.

Система Y ³ является превосходной, несмотря на то, что имеет место соотношение у ⁴₂ > y ³₂> поскольку система Y ⁴ вообще не пригодна и, следовательно, неконкурентоспособна по сравнению с остальными.

Рис. 39. Пример оценок систем по критериям пригодности, оптимальности и превосходства

Легко заметить, что критерий превосходства является частным случаем критерия оптимальности, который, в свою очередь, является частным случаем критерия пригодности, поскольку область адекватности по критерию пригодности представляет собой декартово произведение множеств

по критерию оптимальности вырождается в двухточечное множество < у ^опт₁, y ^опт₂ >, по критерию превосходства вырождается в точку превосходства. Формально К ^прев Ì К ^опт Ì К ^приг.