
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сравнение двух дисперсий нормальных генеральных совокупностейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
По независимым выборкам, объемы которых Требуется сравнить эти дисперсии. Правило 1. Для того чтобы при заданном уровне значимости
и по таблице критических точек распределения Фишера—Снедекора, по заданному уровню значимости Пример 9.3. По двум независимым выборкам, объемы которых Решение: Найдем отношение большей исправленной дисперсии к меньшей:
По таблице (приложение 3), по уровню значимости
находим критическую точку
Так как Правило 2. При конкурирующей гипотезе H1: D(X)
Литература: Гмурман, В. Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов/В. Е. Гмурман. — 9-е изд., стер. — М.: Высш. шк., 2003. — с.281 – 293. Контрольные вопросы: 1. Что вы понимаете под словом «гипотеза»? 2. Какую гипотезу называют статистической? Приведите примеры таких гипотез. 3. Какую гипотезу называют нулевой, конкурирующей, простой, сложной? 4. Сформулируйте основной принцип проверки гипотез. 5. Каким образом происходит сравнение двух дисперсий нормальных генеральных совокупностей?
Задания для самостоятельного решения Задание 9.1. По двум независимым выборкам, объемы которых n1 = 11 и n2 =14, извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии Задание 9.2. По двум независимым выборкам, объемы которых n1 = 9 и n2 =16, извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии Вопросы к экзамену 1. Предмет теории вероятностей. 2. Правила комбинаторики (сложения и произведения). 3. Типы комбинаторных комбинаций. Перестановки. 4. Типы комбинаторных комбинаций. Размещения. 5. Типы комбинаторных комбинаций. Сочетания. 6. Понятие случайного события. 7. Виды случайных событий. 8. Операции над событиями. 9. Классическая вероятность и ее свойства. 10. Алгоритм решения задач на классическую вероятность. 11. Статистическое определение вероятности. 12. Геометрическое определение вероятности. 13. Теоремы сложения вероятностей. 14. Теоремы умножения вероятностей. 15. Формула полной вероятности. Формула Байеса. 16. Формула Бернулли. 17. Локальная теорема Лапласа. 18. Интегральная теорема Лапласа. 19. Понятие случайной величины. 20. Виды случайных величин. 21. Закон распределения вероятностей дискретной случайной величины. 22. Многоугольник распределения. 23. Функция распределения. 24. Математическое ожидание случайной величины. 25. Свойства математического ожидания. 26. Дисперсия случайной величины. Среднее квадратическое отклонение. 27. Свойства дисперсии. 28. Биноминальное распределение. 29. Распределение Пуассона. 30. Равномерное распределение. 31. Нормальное распределение. 32. Понятие о системе нескольких случайных величин. 33. Закон распределения вероятностей дискретной двумерной случайной величины. 34. Функция распределения двумерной случайной величины. 35. Плотность непрерывной двумерной случайной величины.
36. Числовые характеристики непрерывной системы двух случайных величин. 37. Предмет математической статистики. 38. Первичная обработка выборок. Генеральная совокупность и выборка. 39. Основные виды выборок. 40. Способы отбора выборок. 41. Вариационный ряд. 42. Графическое представление вариационных рядов. Гистограмма. 43. Графическое представление вариационных рядов. Полигон частот.
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 987; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.11.146 (0.01 с.) |

 и
и  , извлеченным из нормальных генеральных совокупностей, найдены исправленные выборочные дисперсии
, извлеченным из нормальных генеральных совокупностей, найдены исправленные выборочные дисперсии 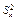 и
и  .
.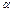 проверить нулевую гипотезу Hо: D(X) = D(Y) о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе H1: D(X)>D(Y), надо вычислить наблюдаемое значение критерия (отношение большей исправленной дисперсии к меньшей):
проверить нулевую гипотезу Hо: D(X) = D(Y) о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе H1: D(X)>D(Y), надо вычислить наблюдаемое значение критерия (отношение большей исправленной дисперсии к меньшей):
 ,
,  (k1 – число степеней свободы большей исправленной дисперсии) найти критическую точку
(k1 – число степеней свободы большей исправленной дисперсии) найти критическую точку  . Если
. Если  нет оснований отвергнуть нулевую гипотезу. Если
нет оснований отвергнуть нулевую гипотезу. Если  – нулевую гипотезу отвергают.
– нулевую гипотезу отвергают. .
. ,
, 
 .
. D(Y), критическую точку
D(Y), критическую точку  ищут по уровню значимости
ищут по уровню значимости  (вдвое меньшему заданного) и числам степеней свободы k1 и k2 (k1 —число степеней свободы большей дисперсии). Если
(вдвое меньшему заданного) и числам степеней свободы k1 и k2 (k1 —число степеней свободы большей дисперсии). Если  = 0,76 и
= 0,76 и  = 0,38. При уровне значимости а = 0,05, проверить нулевую гипотезу Н0: D (X) = D (Y) о равенстве генеральных дисперсий, при конкурирующей гипотезе Н1: D (X) > D (Y).
= 0,38. При уровне значимости а = 0,05, проверить нулевую гипотезу Н0: D (X) = D (Y) о равенстве генеральных дисперсий, при конкурирующей гипотезе Н1: D (X) > D (Y).


