
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормальное распределение и его параметры.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нормальное распределение впервые было найдено Абрахамом де Муавром в первой половине XVIII в. (1733г). Затем в начале XIX в. было использовано в работах Гаусса и Лапласа и, по существу, было открыто заново. Под влиянием классических работ Гаусса и Лапласа долгие годы считалось непререкаемой истиной, что все возможные распределения при достаточно большом количестве наблюдений приближаются к нормальному распределению, как некоему идеалу. Подобное утверждение, безусловно, слишком смелое, но тем не менее множество биологических и медицинских показателей, таких как показатели физического развития (вес, рост, давление, температура тела, уровень гормонов), составляющие плазмы крови, демографические и другие показатели следуют нормальному распределению. Нормальное распределение представляет собой семейство кривых. Каждая кривая это колоколообразный график, на котором по горизонтальной оси откладывается величина эффекта, а на вертикальной – количество пациентов, у которых наблюдался эффект данной величины.
Кривая полностью определяется двумя параметрами, средним и среднеквадратическим отклонением. Факт указанного распределения записывают таким образом:
Основные характеристики нормального распределения: - равенство числовых характеристик собой); - симметричность отклонений от среднего значения; - общая площадь под кривой равна 1; - хвосты кривой в обоих направлениях уходят в бесконечность, непрерывно приближаясь, но, никогда не касаясь, горизонтальной оси, т.е. хвосты асимптотически стремятся к горизонтальной оси; - форма кривой определяется среднеквадратическим отклонением генеральной совокупности; - распределениям с малыми среднеквадратическими отклонениями соответствуют узкие, вытянутые вверх кривые, а распределениям с большими среднеквадратическими отклонениями более пологие кривые с менее выраженными вершинами (малые отклонения более вероятны, большие - менее вероятны);
Правило 3-х сигм 68,25% всех значений лежит в интервале 95,44% всех значений лежит в интервале 99,73% всех значений лежит в интервале
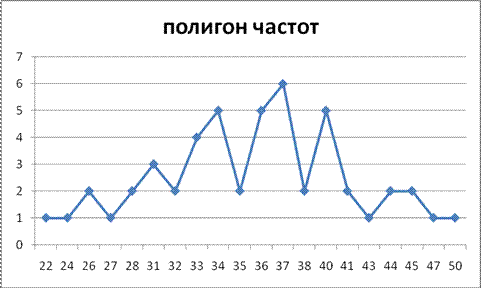
Пример. Из очень большой партии ампул извлечена случайная выборка объема 50 интересующий нас признак Х-длины ампул, измеренные с точностью до 1см, представлен следующим вариоционным рядом: 22, 24, 26, 26, 27, 28, 28, 31, 31, 31, 32, 32, 33, 33, 33, 33, 34, 34, 34, 34, 34, 35, 35, 36, 36, 36, 36, 36, 37, 37, 37, 37, 37, 37, 38, 38, 40, 40, 40, 40, 40, 41, 41, 43, 44, 44, 45, 45, 47, 50. Найти дискретный, интервальный ряды распределения, моду, медиану, выборочную среднюю, дисперсию, среднее квадратическое отклонение, доверительный интервал. Построить полигон частот, гистограмму частот, гистограмму относительных частот. Проверить подчиняется ли выборка нормальному закону распределения (выполнение правила 3-х сигм). Решение. Дискретный статистический ряд распределения
Мода М0=37. Медиана Выборочная средняя
Выборочная дисперсия
Выборочное среднее квадратическое отклонение: Величину отклонения выборочного показателя (статистики) от его генерального параметра называют статистической ошибкой. Для измерения этой ошибки некоторой статистики квадратичная (стандартная) ошибка статистики (нельзя путать со средним квадратичным отклонением изучаемой случайной переменной):
доверительный интервал для выборочного среднего значения находится между границами
Интервальный статистический ряд распределения
Определим количество интервалов по формуле Стерджеса.
Определим величину шага интервала h
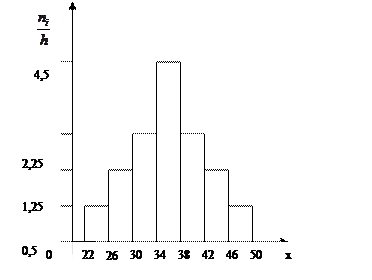
Гистограмма частот
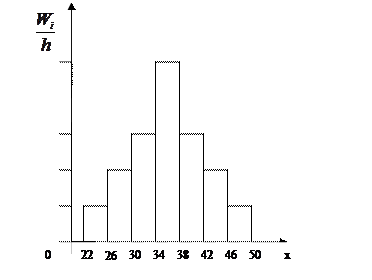
Гистограмма относительных частот

Правило 3-х сигм Ø 68,25% всех значений лежит в интервале Ø 95,44% всех значений лежит в интервале Ø 99,73% всех значений лежит в интервале
Согласно этим данным можно сделать вывод, что выборка распределена нормально.
Задания 1. Изучалось среднее артериальное давление (мм.рт.ст.) в начальной стадии шока. По случайной выборке объема 50: 112, 110, 107, 103, 108, 109, 111, 110, 103, 103, 109. 102, 113, 106, 105, 108, 104, 99, 112, 112, 103, 101, 98, 100, 97. 98. 100, 98, 107, 108, 99, 98, 92, 98, 110, 106, 105, 102, 100, 101, 100, 95, 100, 105, 100, 102, 102, 99, 97, 100. Найти дискретный, интервальный ряды распределения, моду, медиану, выборочную среднюю, дисперсию, среднее квадратическое отклонение, доверительный интервал. Построить полигон частот, гистограмму частот, гистограмму относительных частот. Проверить подчиняется ли выборка нормальному закону распределения (выполнение правила 3-х сигм). 2. Изучался рост (см) мужчин возраста 25 лет для сельской местности. По случайной выборке объема 35: 175, 167. 168, 169, 168, 170,174, 173, 177, 172, 174, 167, 173, 172, 171, 171, 170, 167, 174, 177, 171, 172, 173, 169, 171, 173, 173, 168, 173. 172, 166, 164, 168, 172, 174. Найти дискретный, интервальный ряды распределения, моду, медиану, выборочную среднюю, дисперсию, среднее квадратическое отклонение, доверительный интервал. Построить полигон частот, гистограмму частот, гистограмму относительных частот. Проверить подчиняется ли выборка нормальному закону распределения (выполнение правила 3-х сигм).. 3. Из продукции, произведенной фармацевтической фабрикой за месяц, случайным образом отобраны 15 коробочек некоторого гомеопатического препарата, количество таблеток в которых оказалось равным соответственно 50, 51, 48, 52, 50, 49, 50, 47, 50, 51, 49, 50, 52, 48, 49. Найти дискретный, интервальный ряды распределения, моду, медиану, выборочную среднюю, дисперсию, среднее квадратическое отклонение, доверительный интервал. Построить полигон частот, гистограмму частот, гистограмму относительных частот. Проверить подчиняется ли выборка нормальному закону распределения (выполнение правила 3-х сигм). Литература Основная литература 1. Адибаев Б.М. Элементы математической статистики и основы теории верятностей. Учебное пособие, Алматы 2004г. 2. Баврин И.И. Краткий курс высшей математики. Учебник для химико-биологических и медицинских специальностей. Москва. 2003г. 3. Павлушков И.В. Основы высшей математики и математической статистики. Учебник для медицинских и фармацевтических вузов. М., 2003г. 4. Е.А.Лукьянова Медицинская статистика. Москва. Издательство Россиского университета дружбы народов.2002г. 5. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М., «Высшая школа», 2002г. 6. Гмурман В.Е. Теория вероятностей и математическая статистика. М., «Высшая школа, 2001г. 7. Морозов В.Ю. Основы высшей математики и статистики. Москва. Медицина. 2001г. 8. Турецкий В.Я. Математика и информатика. Москва. ИНФРА-М. 2004г. 9. Ремизов А.Н., Максина А.Г. Сборник задач по медицинской и биологической физике. Москва. 2001г.
Дополнительная литература 1. Чистяков В.П. Курс теории вероятностей. М., «Наука», 1982г.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1628; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.237.229 (0.006 с.) |


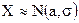 .
.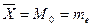 (среднее, мода и медиана равны между
(среднее, мода и медиана равны между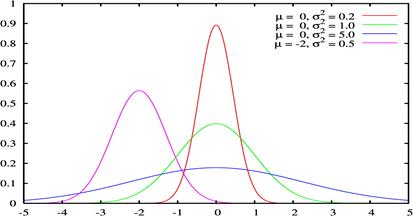
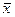 ±σ (±1 среднеквадратическое отклонение от среднего);
±σ (±1 среднеквадратическое отклонение от среднего);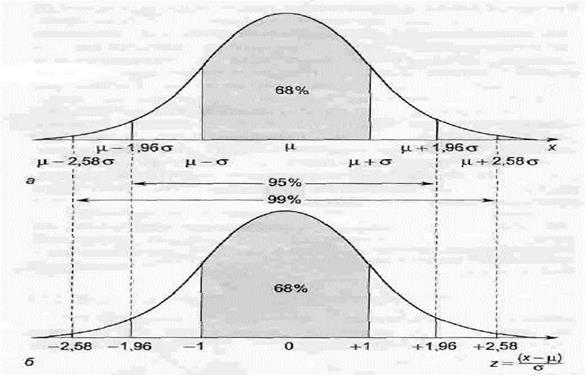
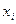
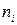
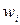
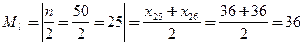

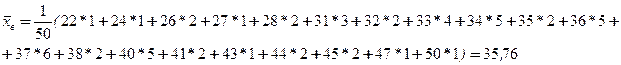
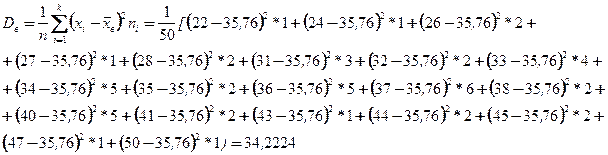
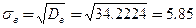 .
.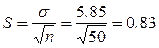
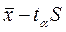 и
и 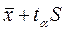 , где
, где 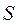 - стандартная ошибка среднего,
- стандартная ошибка среднего, 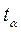 - коэффициент Стьюдента, величина, зависящая от объема выборки
- коэффициент Стьюдента, величина, зависящая от объема выборки 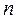 (или соответствующего числа степеней свободы
(или соответствующего числа степеней свободы 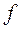 ) и выбранного уровня доверительной вероятности, определяется по таблицам распределений Стьюдента.
) и выбранного уровня доверительной вероятности, определяется по таблицам распределений Стьюдента.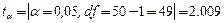
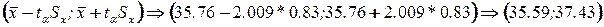
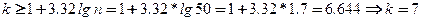 ,
, ,
, 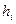 =22+4і, і=0,1,…,7.
=22+4і, і=0,1,…,7.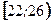

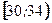
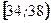
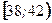
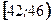
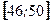
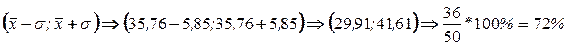 , т.е. в интервале
, т.е. в интервале 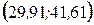 расположено 36 вариант из 50, что составляет 72% от объема выборки.
расположено 36 вариант из 50, что составляет 72% от объема выборки.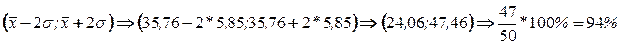 ,
,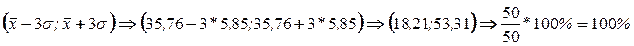 .
.


