
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плотность непрерывной двумерной случайной величиныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Двумерная случайная величина задавалась с помощью функции распределения. Непрерывную двумерную величину можно также задать, пользуясь плотностью распределения. Будем предполагать, что функция распределения F (х, у) всюду непрерывна и имеет всюду (за исключением, быть может, конечного числа кривых) непрерывную частную производную второго порядка. Плотностью совместного распределения вероятностей f(х, у) двумерной непрерывной случайной величины (X, Y) называют вторую смешанную частную производную от функции распределения:
Геометрически эту функцию можно истолковать как поверхность, которую называют поверхностью распределения. Зная плотность распределения, можно найти функцию распределения по формуле:
Вероятность попадания случайной точки (Х,Y) в область D определяется равенством
Числовые характеристики непрерывной системы двух случайных величин Зная плотности распределения составляющих Х и У непрерывной двумерной случайной величины (X, У), можно найти их математические ожидания и дисперсии:
Начальным моментом vk,s порядка k + s системы (X, Y) называют математическое ожидание произведения XkYs: vk,s = М[XkYs]. Центральным моментом µk,s порядка k + s системы (X, Y) называют математическое ожидание произведения отклонений соответственно k-й и s-й степеней: µk,s = М{[X – M(X)]k. [Y –M(Y)]s}. Корреляционным моментом µху системы (X, Y) называют центральный момент µ1,1 порядка 1 + 1: µх,у = М{[X – M(X)]. [Y –M(Y)]}. Коэффициентом корреляции величин X и Y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин:
Коэффициент корреляции служит для оценки тесноты линейной связи между X и Y: чем ближе абсолютная величина коэффициента корреляции к единице, тем связь сильнее; чем ближе абсолютная величина коэффициента корреляции к нулю, тем связь слабее. Коррелированными называют две случайные величины, если их корреляционный момент отличен от нуля. Некоррелированными называют две случайные величины, если их корреляционный момент равен нулю. Литература: Гмурман, В. Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов/В. Е. Гмурман. — 9-е изд., стер. — М.: Высш. шк., 2003. — с.155 – 179. Контрольные вопросы: 1. Какие величины называют двумерными? 2. Что представляет собой закон распределения дискретной двумерной случайной величины? В каком виде он может быть представлен? 3. Как зная закон распределения двумерной дискретной случайной величины, можно найти законы распределения каждой из составляющих? 4. Что представляет собой функцией распределения двумерной случайной величины? 5. Перечислите свойства функции распределения двумерной случайной величины. 6. Что называют плотностью непрерывной двумерной случайной величины? 7. Как отыскать вероятность попадания случайной точки (Х,Y) в область D? 8. Перечислите числовые характеристики непрерывной системы двух случайных величин.
Задания для самостоятельного решения Задание 6.1. Задано распределение вероятностей дискретной двумерной случайной величины:
Найти законы распределения составляющих X и Y. Задание 6.2. В продукции завода брак вследствие дефекта А составляет 10%, а вследствие дефекта B – 20%. Годная продукция составляет 75%. Пусть X – индикатор дефекта А, а Y – индикатор дефекта B. Составить матрицу вероятностей двухмерной случайной величины (X, Y). Найти одномерные ряды распределений составляющих X и Y и исследовать их зависимость. Задание 6.3. Задана плотность совместного распределения непрерывной двумерной случайной величины (X, У): f(х, y)= (1/2) sin (x +y)в квадрате Тема 7 Элементы математической статистики
7.1. Предмет математической статистики. 7.2.Первичная обработка выборок. Генеральная совокупность и выборка. 7.3. Основные виды выборок. 7.4. Способы отбора. 7.5. Вариационный ряд. 7.6. Графическое представление вариационных рядов. Эмпирическая функция распределения. Числовые характеристики выборки.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 970; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.88.132 (0.008 с.) |





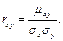
 вне квадрата f(x, у) = 0. Найти математические ожидания и дисперсии составляющих.
вне квадрата f(x, у) = 0. Найти математические ожидания и дисперсии составляющих.


