
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ответ №1 Операции над случайными событиями.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ответ №1 Операции над случайными событиями. 1. Ᾱ - читается «не А», означает, что событие А не произошло. Р(Ᾱ) + Р(А) = 1 2. Сумма двух событий. А + В – читается как «А или В» Суммой двух случайных событий называется случайное событие, что произойдёт хотя бы одно из двух. А + В = В + А А + А = А А + Ø = А А + Ω = Ω Если два случайных события несовместны, то: Р(А+В) = Р(А) + Р(В) 3. Произведение двух случайных событий. А • В – читается как «А и В» Произведение двух случайных событий называется случайное событие, в котором совпадают оба события. Независимые события не могут произойти вместе, следовательно = Ø А • В = В • А А • А = А А • Ø = Ø А • Ω = А А • (В+С) = АВ + АС
4. Формула сложения вероятностей, когда совместны: Р(А + В) = Р(А) + Р(В) – Р(А •В) Не путать с формулой, когда события несовместны!!! 5. А\В – разность событий. Если событие А наступает, то событие В нет. В\А = В •
Ответ №2 Классическая модель Т.В. Формулы комбинаторики. 1. Классическая модель: А – случайное событие n – все исходы m – благоприятствующие исходы Р(А) = m ÷ n 2. Пусть множествоА состоит из k элементов:A = {a1, …, ak}, а множество B — из m элементов:B = {b1, …,bm}. Тогда можно образовать ровно km пар (ai, bj), взяв первый элемент из множества A, а второй — из множества B. o Выбор с возвращением: каждый вынутый шар возвращается в урну, каждый следующий шар выбирается из полной урны. В полученном наборе из номеров шаров могут встречаться одни и те же номера. o Выбор без возвращения: вынутые шары в урну не возвращаются, и в полученном наборе не могут встречаться одни и те же номера. o Выбор с учётом порядка: два набора номеров шаров считаются различными, если они отличаются составом или порядком номеров. Так, при выборе трёх шаров из урны, содержащей 5 шаров, наборы (1, 5, 2), (2, 5, 1) и (4, 4, 5) различны, если порядок учитывается. o Выбор без учёта порядка: два набора номеров шаров считаются различными, если они отличаются составом. Наборы, отличающиеся лишь порядком следования номеров, считаются одинаковыми. o Так, наборы (1, 5, 2) и (2, 5, 1) не различаются и образуют один и тот же результат выбора, если порядок не учитывается. 3. А) Число размещений из n по k элементов (общее кол-во различных наборов при выборе kэлементов из n без повтора)
Б) С повтором:
4. Число сочетаний (Общее количество различных наборов при выборе k элементов из n без возвращения и без учёта порядка равняется)
Свойства:
5. Общее количество различных наборов при выборе k элементов из n с возвращением и с учётом порядка равняется nk. 6. Комбинаторика – изуч кол-во комбинаций, подчиненных опред условиям, кот можно составить из эл-тов заданного конечного множества. Перестановки – комбинации, сост из одних и тех же n различных элементов и отл только порядком расположения. Число всех возм переест= Рn=n!. Размещения – комбинации, сост из n разл эл-тов по m эл-тов, отл составом или порядком. Аmn=n(n-1)(n-2)…(n-m+1). Сочетания – комбинации, сост из n различных эл-тов по m эл-тов, кот отл хотяб 1 эл-том. Cmn=n!/(m!(n-m)!). 7. А=Р*С. Если n повторяются, то Pn(n1,n2,…)= n!/(n1!*n2!*…), n1+n2+…=n.
Ответ №3 Вероятность суммы двух случайных событий. Несовместные события. Существует две формулы суммы двух случайных событий – когда они совместны и когда они несовместны. Когда они совместны:
Когда несовместны:
Вероятность события А+В определяется отношением меры области|A+B|, составленной из двух подобластей А и В, к мере всей области G. Мера двух областей А и В равна сумме мер каждой области: |A+B| = |A|+|B|. Поэтому вероятность события А+В также равна сумме вероятностей двух событий:P(A+B)=|A+B|÷|G| = |A|÷|G| + |B|÷|G| = P(A) + P(B).
Ответ №4 Условная вероятность события. Формула умножения вероятностей. Независимые события.
Формула умножения вероятностей:
События А, В В противном случае события А и В называются зависимыми.
Ответ №5 Формула полной вероятности. Применяется для определения вероятности ещё не наступившего события.
Н1, Н2,…, Нn – гипотеза. Гипотезы – события, совершённые до основного события. Нi • Hj = Ø – две противоположные гипотезы. Н1 + Н2 +…+ Нn = Ω Р(Н1)+Р(Н2)+…+Р(Нn) = 1
Формула Байеса. Формула Байеса позволяет переоценить вероятность гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А. Если событие А может произойти только при выполнении одного из событий
Эта формула называется формулой полной вероятности. Вновь рассмотрим полную группу несовместных событий Если событие А произошло, то это может изменить вероятности гипотез По теореме умножения вероятностей
Таблица распределения дискретной С.В. Таблица совместного распределения двух дискретных С.В. Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены. Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным. Таблица распределения дискретной С.В – это закон распределения дискретной С.В., представленный в виде таблицы, чтобы показать соответствие между возможными значениями и их вероятностями (Биномиальный закон). Биномиальным называют закон распределения дискретной случайной величины X - числа появлений события в n независимых испытаниях, в каждом из которых вероятность наступления события постоянна. Вероятности pi вычисляют по формуле Бернулли
Для биномиального распределения: математическое ожидание M(X) = np, дисперсия D(X) = npq, мода np-q ≤ Mo ≤ np+p n – число испытаний, p – удачи, q – неудачи
Таблица совместного распределения двух дискретных С.В. Законом распределения дискретной двумерной С.В. называют перечень возможных значений этой величины (т.е. пар чисел (хi, yj) и их вероятностей р(хi, yj) (i=1,2,…,n; j=1,2,…,m)). Обычно закон распределения задают в виде таблицы с двойным входом.
Первая строка таблицы содержит все возможные значения составляющей Х, а первый столбец – все возможные значения составляющей Y. В клетке, стоящей напересечений «столбца хi» и «строки yj», указана вероятность того, что двумерная случайная величина примет значение (хi, yj).
Так как события (Х= хi,Y= yj) (i=1,2,…,n; j=1,2,…,m) образуют полную группу, то сумма вероятностей, помещенных во всех клетках таблицы равна единице.
Зная закон распределения двумерной дискретной случайной величины, можно найти законы распределения каждой из составляющих. Действительно, например, события (Х= х1,Y= y1), (Х= х2,Y= y2),…, (Х= хn,Y= ym) несовместны, поэтому вероятность p(x1) того, что X примет значение x1 такова:
Таким образом, вероятность того, что X примет значение x1, равна сумме вероятностей «столбца хi». В общем случае, для того, чтобы найти вероятность P(Х= х1), надо просуммировать вероятности столбца хi. Аналогично сложив вероятности «строки yj», получим вероятность P(Y= yj). Ответ №1 Операции над случайными событиями. 1. Ᾱ - читается «не А», означает, что событие А не произошло. Р(Ᾱ) + Р(А) = 1 2. Сумма двух событий. А + В – читается как «А или В» Суммой двух случайных событий называется случайное событие, что произойдёт хотя бы одно из двух. А + В = В + А А + А = А А + Ø = А А + Ω = Ω Если два случайных события несовместны, то:
Р(А+В) = Р(А) + Р(В) 3. Произведение двух случайных событий. А • В – читается как «А и В» Произведение двух случайных событий называется случайное событие, в котором совпадают оба события. Независимые события не могут произойти вместе, следовательно = Ø А • В = В • А А • А = А А • Ø = Ø А • Ω = А А • (В+С) = АВ + АС
4. Формула сложения вероятностей, когда совместны: Р(А + В) = Р(А) + Р(В) – Р(А •В) Не путать с формулой, когда события несовместны!!! 5. А\В – разность событий. Если событие А наступает, то событие В нет. В\А = В •
|
|||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 633; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.244.75 (0.01 с.) |





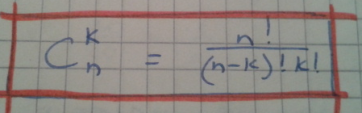

 Р(А + В) = Р(А) + Р(В) – Р (А •В)
Р(А + В) = Р(А) + Р(В) – Р (А •В) Р(А+В) = Р(А) + Р(В)
Р(А+В) = Р(А) + Р(В)



 Е называются независимыми, если Р (А • В) = Р (А) · Р (В).
Е называются независимыми, если Р (А • В) = Р (А) · Р (В).
 , которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле
, которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле 
 . Событие А может произойти только вместе с каким-либо из событий
. Событие А может произойти только вместе с каким-либо из событий  откуда
откуда 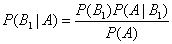 .
.





