
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ответ №16 Нормальный закон распределения.Содержание книги
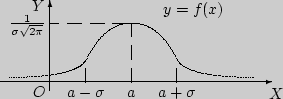
Поиск на нашем сайте Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности Нормальный закон распределения также называется законом Гаусса. График плотности нормального распределения называется нормальной кривой или кривой Гаусса. Нормальная кривая обладает следующими свойствами: 1) Функция определена на всей числовой ос 2) При всех х функция распределения принимает только положительные значения. 3) Ось ОХ является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по абсолютной величине аргумента х, значение функции стремится к нулю. 4) х1 = а – σ, х2 = а + σ – точки перегиба.
- параметры
f(x) – плотность распределения. F(x) –функция распределения. Она равна интегралу от f(x). Ответ №17 Предельные теоремы теории вероятностей. Интегральная теорема Муавра-Лапласа. В конце 19 века в теории вероятностей возникло направление исследований, которое получило название: предельные теоремы теории вероятностей. В этом направлении, начало которого было положено нашими соотечественниками П.Л.Чебышевым, А.А.Марковым, А.М.Ляпуновым, по сей день ведутся интенсивные исследования. Предельные теоремы теории вероятностей можно разбить на две большие группы. 1. Одна группа теорем составляет "закон больших чисел". Закон больших чисел формулирует условия, при которых совокупное действие большого числа случайных факторов приводит к результату почти не зависящему от случая (т.е. практически постоянный результат) 2. Вторая группа теорем связана с выяснением вопроса о распределении сумм большого числа случайных величин. В этих теоремах выясняется, какие законы распределения может иметь сумма случайных величин, если число слагаемых неограниченно увеличивается, и какие условия при этом нужно наложить на сами величины. В частности, центральная предельная теорема посвящена установлению сумм, при которых возникает нормальный закон распределения. · Центральная предельная теорема Первый вариант этой теоремы был доказан в 1912 г. А.М.Ляпуновым. · Интегральная теорема Лапласа.
, где а – Мат. ожидание. · Неравенство Чебышева. Каково бы ни было положительное число А вероятность того, что случайная величина отклонится от своего математического ожидания не меньше, чем на А, ограничена сверху величиной D(X)÷a2, т.е. P(|X – M(x)|<a) ≥ 1 – D(x) ÷ a2,где а – какое-то число, которое будет дано. · Теорема Чебышева. Пусть наблюдается одна и та же случайная величина X с математическим ожиданием М(Х) и дисперсией D(X)<∞. Обозначим через X1,X2,…,Xn результат первого наблюдения, второго наблюдения и т.д. При увеличении числа независимых опытов n среднее арифметическое наблюдаемых значений случайной величины сходится по вероятности к ее математическому ожиданию, т.е.
Применяется, если нужно проделать достаточно много наблюдений случайной величины и вычислить среднее арифметическое наблюденных значений. · Теорема Бернулли.
Показывается вероятность того, что частота появления случайного события в серии Nиспытаний отклоняется от вероятности Р того события, на определённую величину большую, чем е, стремится к 0. Интегральная теорема Муавра – Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность того, что в n независимых испытаниях событие А состоится число раз, заключенное в границах от а до b включительно (а <b), приближенно равна:
где функция Ф (х) определяется равенством
1. Функция Ф(х) нечетная, т. е. Ф (—х) = — Ф(х). 2. Функция Ф(х) монотонно возрастающая. 3. Предел функции Ф(х) при
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 358; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

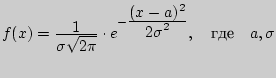
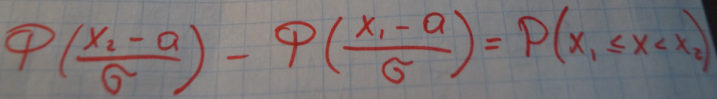 Пусть X есть число наступлений события в n независимых опытах, в каждом из которых вероятность появления события равнаp|0<p<1|.Тогда при достаточно больших n вероятность того, что событие появится от x1 до x2 раз равна:
Пусть X есть число наступлений события в n независимых опытах, в каждом из которых вероятность появления события равнаp|0<p<1|.Тогда при достаточно больших n вероятность того, что событие появится от x1 до x2 раз равна: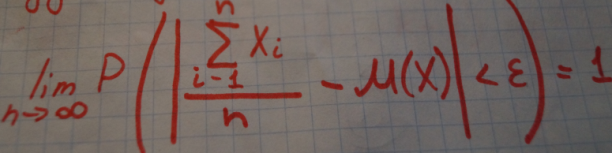 - Теорема Чебышева
- Теорема Чебышева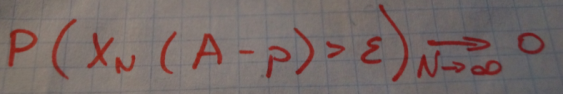
 ,
, ,
,
 равен единице.
равен единице.


