Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двумерная случайная величинаСодержание книги
Поиск на нашем сайте Определение 10. Упорядоченная пара случайных величин (Х; Y) называется двумерной случайной величиной. Определение 11. Возможным значением двумерной случайной величины (Х; Y) называется упорядоченная пара чисел вида (Х = xi; Y = yj), а ее вероятностью – вероятность события (Х = xi; Y = yj): pij = p (Х = xi; Y = yj). Определение 12. Законом распределения двумерной случайной величины называется перечень возможных значений (xi; yj) этой величины и их вероятностей pij (i = 1,2,…, m; j = 1,2,…, n). Обычно двумерное распределение задается в виде таблицы
Так как события (Х = xi; Y = yj), где i = 1,2,…, m и j = 1,2,…, n, образуют полную группу, то сумма вероятностей pij в данной таблице равна 1. Безусловные вероятности дискретных компонент Х и Y находятся по формулам
Для условных вероятностей компонент Х и Y справедливы формулы:
Математические ожидания компонент Х и Y находятся следующим образом:
Определение 13. Ковариацией (корреляционным моментом) компонент Х и Y называется математическое ожидание произведения отклонений этих величин от своих математических ожиданий:
 (суммирование производится по всем возможным парам индексов ij). (суммирование производится по всем возможным парам индексов ij).
Пусть дана случайная величина Z = X + Y. Тогда математическое ожидание M (Z) = M (X) + M (Y), (14), а дисперсия D (Z) = M (Z 2) – M 2(Z). (15) Задача. Дана дискретная двумерная случайная величина 1) безусловные законы распределения компонент Х и Y; 2) математические ожидания составляющих компонент M (X), M (Y) и центр рассеяния 3) условный закон распределения X при Y = 1 и найти M (X /Y = 1); 4) закон распределения случайной величины T = 3 X + 1, математическое ожидание M (T) и дисперсию D (T); 5) закон распределения случайной величины Z = X + Y; математическое ожидание M (Z) и дисперсию D (Z); 6) построить график интегральной функции распределения F (Z) случайной величины Z.
Решение. 1) Согласно (10), складывая вдоль строк (по индексу j) и вдоль столбцов (по индексу i), получим безусловные вероятности соответствующих значений xi и yj случайных компонент вектора
2) Согласно (12) и результатам пункта 1 математическое ожидание компонент: M (X) = 1×0,25 + 2×0,3 + 3×0,25 + 4×0,2 = 2,4; M (Y) = –1×0,25 + 0×0,3 + 1×0,45 = 0,2.  . .
Найдем «исправленное» среднее квадратическое отклонение
Найдем наблюдаемое значение критерия:
Табулированное значение tдвуст.кр. (a = 0,05; k = n – 1) = 2,57. Так как
Правило. Для того чтобы при заданном уравнении значимости a проверить нулевую гипотезу
и по таблице критических точек распределения Стьюдента, по заданному уровню значимости Задача. Двумя приборами в одном и том же порядке измерены шесть деталей и получены следующие результаты измерений (в сотых долях миллиметра):
При уровне значимости 0,05 установить, значимо или незначимо различаются результаты измерений, в предположении, что они распределены нормально. Решение. Найдем разности Найдем выборочную среднюю, учитывая, что Согласно (13) для нахождения ковариации компонент вектора M (XY) = –1×2×0,1 –1×3×0,1–1×4×0,05+1×1×0,2+1×2×0,1+1×4×0,15 = 0,3. Следовательно, cov (X, Y) = M (XY) – M (X)× M (Y) = 0,3 – 2,4×0,2 = – 0,18. 3) Согласно (11) и результатам пункта 1 получим условные вероятности
Таким образом, условный закон распределения случайной компоненты X при Y = 3 можно представить таблицей:
(столбец с вероятностью равной 0 можно опустить). Найдем математическое ожидание M (X /Y = 1) = 1×0,45 + 2×0,22 + 3×0 + 4×0,33 = 2,21. 4) Значения случайной величины T = 3 X + 1 получаются при подстановке значений случайной величины X в формулу для Т; а их вероятности совпадают с соответствующими вероятностями значений случайной величины Х:
Найдем М (Т) и D (T):
5) Для определения закона распределения случайной величины Z = X + Y предварительно составим таблицу возможных значений Z, задаваемых значениями xi + yj, и вероятностей этих значений, равных p (Х = xi; Y = yj)= pij:
Упорядочим запись закона распределения случайной величины Z, причем вероятности одинаковых значений необходимо сложить:
(столбцы с нулевыми вероятностями можно опустить). Найдем M (Z) и D (Z): M (Z) = 1×0,15 + 2×0,4 + 3×0,3 + 5×0,15 = 2,6 или M (Z) = М (X + Y) = M (X) + M (Y) = 2,4 + 0,2 = 2,6; D (Z) = 12×0,15 + 22×0,4 + 32×0,3 + 52×0,15 – 2,62 = 1,44. 6) Используя полученный закон распределения случайной величины Z, построим график (рис. 3) интегрального закона распределения F (z) =p (Z<z) с учетом того, что функция F (z) принимает значения:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.007 с.) |

 Y
X
Y
X
 (10)
(10) (11)
(11) (12)
(12) (13)
(13) = (Х; Y). Найти:
= (Х; Y). Найти: ; ковариацию компонент cov (X, Y);
; ковариацию компонент cov (X, Y);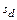 , учитывая, что
, учитывая, что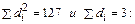


 – нет оснований отвергать нулевую гипотезу. Другими словами, средние результаты измерений различаются незначимо.
– нет оснований отвергать нулевую гипотезу. Другими словами, средние результаты измерений различаются незначимо. - «исправленное» среднее квадратическое отклонение.
- «исправленное» среднее квадратическое отклонение.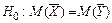 о равенстве двух средних нормальных совокупностей X и Y с неизвестными дисперсиями (в случае зависимых выборок одинакового объема) при конкурирующей гипотезе
о равенстве двух средних нормальных совокупностей X и Y с неизвестными дисперсиями (в случае зависимых выборок одинакового объема) при конкурирующей гипотезе  , надо вычислить наблюдаемое значение критерия:
, надо вычислить наблюдаемое значение критерия: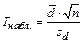
 , помещенному в верхней строке таблицы, и числу степеней свободы k = n – 1 найти критическую точку
, помещенному в верхней строке таблицы, и числу степеней свободы k = n – 1 найти критическую точку 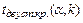 . Если
. Если  – нет оснований отвергать нулевую гипотезу. Если
– нет оснований отвергать нулевую гипотезу. Если  – нулевую гипотезу отвергают.
– нулевую гипотезу отвергают.


 , вычитая из чисел первой строки числа второй.
, вычитая из чисел первой строки числа второй. :
: 
 надо знать M (XY). Используя исходную таблицу и опуская слагаемые, содержащие равные 0 множители, получим:
надо знать M (XY). Используя исходную таблицу и опуская слагаемые, содержащие равные 0 множители, получим: