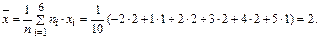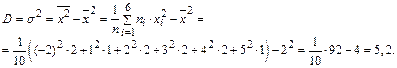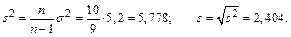Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
статистического распределения выборкиСодержание книги
Поиск на нашем сайте
Определение 17. Выборочное среднее
Определение 18. Выборочной дисперсией D называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения
Дисперсию можно рассчитать по формуле:
Определение 19. Выборочным средним квадратическим отклонением называется величина
Точечные оценки Определение 20. Статистической оценкой неизвестного параметра генеральной совокупности называется приближенное значение, полученное по данным выборки. Определение 21. Точечная оценка – оценка, которая определяется одним числом q. Это точка на числовой оси, около которой находится оцениваемый параметр генеральной совокупности q 0. Определение 23. Оценка q параметра q 0 называется состоятельной, если для любого положительного d Определение 24. Оценка q параметра q 0 называется эффективной, если она является несмещенной и имеет наименьшую дисперсию при заданном объеме выборки. Теорема 5. Выборочное среднее – несмещенная, состоятельная и эффективная оценка математического ожидания признака генеральной совокупности. Теорема 6. Дисперсия выборочного среднего в n раз меньше дисперсии генеральной совокупности:
Теорема 7. Математическое ожидание выборочной дисперсии рассчитывается по формуле
Следовательно, дисперсия выборочного среднего является смещенной оценкой генеральной дисперсии. Чтобы получить несмещенную оценку вводится исправленная дисперсия:
Интервальные оценки Определение 25. Интервал (q – d, q + d), в пределах которого с вероятностью g находится оцениваемый параметр генеральной совокупности q 0, называется доверительным интервалом. Значение g называется доверительной вероятностью или надежностью оценки; предельная погрешность d – точность оценки. Доверительный интервал для оценки математического ожидания нормального распределения определяется следующим образом:
причем, если стандартное отклонение этого распределения известно, то
Здесь число t определяется из равенства F (t) = g / 2; tg находится по таблице коэффициентов Стьюдента при заданных n и g (таблица № 4 Приложений); s – исправленное выборочное среднее квадратическое отклонение. Интервальной оценкой (с надежностью g) стандартного отклонения s 0 нормально распределенного количественного признака X по исправленному выборочному стандартному отклонению s служит доверительный интервал s ×(1 – q) < s 0 < s ×(1 + q) при q < 1, 0 < s 0 < s ×(1 + q) при q > 1, где q = q (n;g) определяется по таблице № 5 Приложений. Задача. По данным выборки найти доверительные интервалы для оценок с надежностью g = 0,95 неизвестных математического ожидания a и стандартного отклонения s нормально распределенного признака X генеральной совокупности. Построить полигон частот по данным выборки:
Решение. 1) Найдем объем выборки
2) Найдем выборочную среднюю
3) Вычислим дисперсию
4) Вычислим «исправленную» дисперсию и «исправленное» стандартное отклонение
5)
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 220; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.81.114 (0.01 с.) |

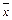 – среднее арифметическое значение признака выборочной совокупности
– среднее арифметическое значение признака выборочной совокупности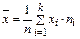 .
.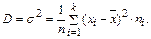
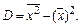
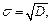 характеризующая отклонение, разброс в линейных размерах данных выборки относительно выборочного среднего.
характеризующая отклонение, разброс в линейных размерах данных выборки относительно выборочного среднего.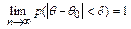 , то есть q стремится к q 0 по вероятности и означает неограниченное увеличение точности с ростом объема выборки.
, то есть q стремится к q 0 по вероятности и означает неограниченное увеличение точности с ростом объема выборки.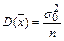 .
. .
. .
.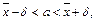
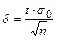 ;
;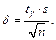
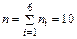 .
.