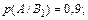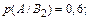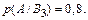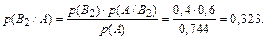Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
II. Формула полной вероятности и формула БайесаСодержание книги
Поиск на нашем сайте
Пусть гипотезы В 1, В 2, …, Вn образуют полную группу событий и попарно несовместны, а событие A может наступить лишь в результате осуществления одной из гипотез
где p (В 1) + p (В 2)+…+ p (Вn) = 1. Допустим, произведено испытание, в результате которого появилось событие А. Вероятности гипотез Вi после опыта, т.е. условные вероятности: р (А/В 1), р (А/В 2 ), …, р (А/Вn), вычисляются по формуле Байеса:
Эта формула позволяет оценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А. Задача 1. После вакцинирования животное в период эпидемии заболевает с вероятностью 0,01, а не вакцинированное – 0,8. Вакцинировано 70% животных. Найти вероятность того, что во время эпидемии животное заболеет. Решение. Обозначим событие А = {животное заболеет}. Возможны следующие гипотезы: В 1 = {животное вакцинировано}, В 2 = {животное не вакцинировано}. Гипотезы В 1, В 2 несовместны и образуют полную группу событий. По условию задачи вероятности этих гипотез: р (В 1) = 0,7, р (В 2) = 0,3. Условная вероятность того, что животное заболеет, если оно вакцинировано р (В 1/ А) = 0,01, а условная вероятность того, что животное заболеет, если оно не вакцинировано р (В 2/ А) = 0,8. Вероятность события А определяется по формуле полной вероятности: р (А) = р (В 1)· р (В 1/ А) + р (В 2)· р (В 2/ А) = 0,7·0,01 + 0,3·0,8 = 0,247. Ответ: р (А) = 0,247.
Задача 2. В ящике содержится 12 деталей завода №1, 20 деталей завода №2, 18 деталей завода №3. Завод №1 выпускает 90% продукции отличного качества, завод №2 – 60%, а завод №3 – 80% продукции отличного качества. Извлеченная наудачу из ящика деталь оказалась отличного качества. Найти вероятность того, что она изготовлена на заводе №2. Решение. Обозначим событие А ={наудачу взятая из ящика деталь окажется отличного качества}. Возможны следующие гипотезы: В 1 = {деталь изготовлена на i -м заводе},
9.5.
9.6.
9.7.
9.8.
9.9.
Задача 9. Линии регрессии.
Найти выборочное уравнение прямой линии регрессии Y на X по данным, приведенным в корреляционной таблице.
9.1.
9.2.
9.3.
9.4.
Условные вероятности того, что деталь окажется отличного качества, если она изготовлена на i -м заводе ( По формуле полной вероятности (2): р (А) = 0,24∙0,9 + 0,4∙0,6 + 0,36∙0,8 = 0,744. По формуле Байеса (3) найдем вероятность того, что извлеченная деталь изготовлена на заводе №2:
Ответ: р (В 2 / А) = 0,323.
III. Схема Бернулли
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 367; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.128.70 (0.008 с.) |

 . Тогда вероятность события А равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А:
. Тогда вероятность события А равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А: (2)
(2) (3)
(3) Гипотезы В 1, В 2, В 3 попарно несовместны и образуют полную группу событий. Поскольку в ящике всего 22+20+18 = 50 деталей, то по классической формуле вероятности:
Гипотезы В 1, В 2, В 3 попарно несовместны и образуют полную группу событий. Поскольку в ящике всего 22+20+18 = 50 деталей, то по классической формуле вероятности: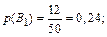
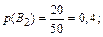

 ) по условию задачи равны:
) по условию задачи равны: