
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывные случайные величины.Содержание книги Поиск на нашем сайте
Плотность распределения непрерывной случайной величины
Вычислить: параметр
Нормальное распределение. Вес изделия является случайной величиной, которая имеет нормальное распределение со средним значением 106 кг и дисперсией 9 кг2. Найти вероятность того, что: а) вес изделия находится в пределах от 100 до 110 кг. б) вес изделия отличается от среднего не более чем на 2 кг.
Обработка статистических данных По заданным выборочным значениям признака Х 1) составить вариационный ряд; 2) вычислить относительные частоты; 3) построить полигон частот; 4) найти эмпирическую функцию распределения и построить ее график; 5) вычислить числовые характеристики выборки: среднее выборочное значение
Уравнение линейной регрессии По заданным выборочным значениям пары признаков Х, У 1) построить корреляционное поле для двумерной выборки; 2) найти коэффициент корреляции между Х и У и сделать вывод о связи признаков Х и У; 3) составить уравнение линейной регрессии У на Х и нанести линию регрессии на корреляционное поле.
Утверждено на заседании кафедры ВПМиИ Протокол №___ от _____________г.
Заведующий кафедры проф. Левин В.М. Донбасская национальная академия строительства и архитектуры
Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 ТЕОРИЯ ВЕРОЯТНОСТЕЙ И ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ Вариант 3.
Классическое определение вероятности. В партии из 12 изделий 4 бракованных. Наудачу выбирают 3 изделия. Определить вероятность того, что: а) среди этих трех изделий будет 2 бракованных; б) среди трех изделий хотя бы одно будет бракованным.
Теоремы сложения и умножения вероятностей. Рабочий обслуживает 3 станка. Вероятность того, что на протяжении часа станок не будет требовать внимания рабочего, равняется для первого станка 0,9, для второго - 0,85, для третьего 0,95. Найти вероятность того, что: а) в течение некоторого часа ни один станок не будет требовать внимания рабочего; б) все станки будут требовать внимания рабочего.
Формула полной вероятности и формула Байеса. В специализированную больницу приходят больные с заболеванием А - 70% больных и заболеванием В - 30 %. Заболевание А полностью излечивается с вероятностью 0,8, заболевание В с вероятностью 0,9. Больной, который поступил в больницу, вылечился. Найти вероятность, что он болел заболеванием А.
Схема Бернулли. Предельные теоремы в схеме Бернулли. Вероятность появления события в каждом испытании равняется 0,25. Найти вероятности: а) в 6 испытаниях событие появится 3 раза; б) в 80 испытаниях событие появится 25 раз; в) в 80 испытаниях событие появится на менее 15 раз.
Дискретные случайные величины. Закон распределения дискретной случайной величины имеет вид:
Найти: Непрерывные случайные величины. Функция распределения случайной величины
Найти: плотность распределения, Нормальное распределение. Плотность распределения случайной величины имеет вид:
Найти: Обработка статистических данных По заданным выборочным значениям признака Х 1) составить вариационный ряд; 2) вычислить относительные частоты; 3) построить полигон частот; 4) найти эмпирическую функцию распределения и построить ее график; 5) вычислить числовые характеристики выборки: среднее выборочное значение
Уравнение линейной регрессии По заданным выборочным значениям пары признаков Х, У 1) построить корреляционное поле для двумерной выборки; 2) найти коэффициент корреляции между Х и У и сделать вывод о связи признаков Х и У; 3) составить уравнение линейной регрессии У на Х и нанести линию регрессии на корреляционное поле.
Утверждено на заседании кафедры ВПМиИ Протокол №___ от _____________г.
Заведующий кафедры проф. Левин В.М. Донбасская национальная академия строительства и архитектуры
Семестр ІІ Учебная дисциплина «Прикладная математика»
Типовой расчет №9 ТЕОРИЯ ВЕРОЯТНОСТЕЙ И ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ Вариант 4.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 259; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.166.141 (0.006 с.) |

 имеет вид:
имеет вид:
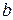 ,
, 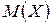 ,
,  ,
,  .
.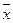 , исправленную выборочную дисперсию
, исправленную выборочную дисперсию  , исправленное среднее квадратическое отклонение
, исправленное среднее квадратическое отклонение  , моду Мо и медиану Ме.
, моду Мо и медиану Ме.
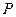

 ,
,  ,
,  ,
,  ,
,  ,
, 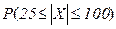 .
.

 ,
, 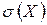 ,
,  ,
,  .
.
 ,
,  .
.


