
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
IV. Теория вероятности и математическаяСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
IV. ТЕОРИЯ ВЕРОЯТНОСТИ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА Справочный материал и принципы решения задач Элементы комбинаторики Пусть дано множество Первый способ выбора элементов приводит к понятиям перестановок, размещений и сочетаний без повторений или просто перестановок, размещений и сочетаний; второй – к понятиям перестановок, размещений и сочетаний с повторениями. Перестановкой из
Размещением из Число размещений вычисляется по формуле Сочетанием из Число сочетаний
Свойства сочетаний:
Пример 8. Пусть имеется множество Размещения и сочетания с повторениями отличаются от размещений и сочетаний без повторений только тем, что в этих соединениях могут присутствовать повторяющиеся элементы. Число размещений из Число сочетаний из Поскольку в таком виде соединений как перестановки с повторениями участвуют все элементы множества
При решении комбинаторных задач могут быть полезны следующие два правила:
Пример 9. Пусть имеется
Если Пример 10. Преподаватель предлагает каждому из трех студентов задумать любое число от 1 до 10. Считая, что выбор каждым студентом любого числа из заданных равновозможен, найти вероятность того, что у кого-то из троих задуманные числа совпадут. Решение. Вначале посчитаем общее количество исходов. Первый из студентов выбирает одно из 10 чисел, Пример 11. По линии связи в случайном порядке передаются все буквы русского алфавита. Найти вероятность того, что на ленте появится последовательность букв, которая начинается словом «мир». Решение. Русский алфавит содержит 33 буквы. Так как по линии связи передаются все буквы, то число равновозможных исходов опыта
Следовательно,
Пример 12. Из урны, содержащей 3 шара, три раза наудачу вынимается по одному шару с возвращением каждый раз обратно. Найти вероятность того, что в руке перебывают все шары. Решение. По условию задачи шары возвращаются в урну, следовательно, имеем схему выбора элементов с возвращением. Число всех возможных исходов данного опыта – это число размещений из трех элементов по три с повторениями, то есть
Благоприятными событию A ={
Пример 13. Технический контроль проверяет из партии в 500 деталей 20 деталей, взятых наудачу. Партия содержит 15 нестандартных деталей. Какова вероятность того, что среди проверяемых деталей будет ровно две нестандартные? Решение. Так как по условию задачи 20 деталей из 500 извлекаются наудачу, то все возможные варианты извлечения 20 деталей из 500 естественно считать равновозможными и для нахождения требуемой вероятности воспользоваться классической схемой (классическим определением вероятности). Порядок следования стандартных и нестандартных деталей в извлекаемых 20 не играет роли. Важно только количество стандартных и нестандартных деталей. Следовательно, количество всех возможных способов, которыми это можно сделать, равно Событию
Пример 14. Трехзначное число составляется следующим образом: бросаются три игральные кости: белая, синяя и красная; число выпавших очков на белой кости – это число сотен, число выпавших очков на синей кости – это число десятков, а число выпавших очков на красной кости – это число единиц трехзначного числа. Какова вероятность того, что полученное таким образом число будет больше 456? Решение. Количество всех чисел, которые можно получить указанным способом, в соответствие с правилом произведения, будет равно Посчитаем количество исходов опыта, благоприятных появлению события А. Числа, большие 456, будут получаться, если число сотен будет больше 4, то есть 5 или 6 или число сотен будет равно 4, а число десятков будет больше чем 5, то есть 6. Пусть число сотен будет равно 5. Таких опытов будет Пример 15. Трем радиостанциям разрешена работа на шести различных частотах. Определить вероятность того, что, по крайней мере, две радиостанции будут работать на одинаковых частотах, если выбор частот производится наугад. Решение. Число всех равновозможных исходов опыта – это число размещений из шести элементов (частот) по три с повторениями, то есть
Таким образом, Следовательно,
Примеры распределений дискретных случайных величин
Примеры распределений непрерывных случайных величин
Запись
Здесь Пример 1. Изделия испытываются при перегрузочных режимах. Вероятности для каждого изделия пройти испытания, равны 0,8. Испытания заканчиваются после первого же изделия, не выдержавшего испытания. 1. Найти закон распределения вероятностей (ряд распределения) для числа испытаний (случайной величины 2. Построить многоугольник распределения. 3. Найти функцию распределения и построить её график. 4. Найти: а) Решение. Введем в рассмотрение случайную величину Случайная величина Закон распределения вероятностей будет иметь вид
Для построения многоугольника распределения в декартовой прямоугольной системе координат построим точки
3. Функция распределения
Для решаемой задачи Строим график функции распределения
4. а)
б) в) Пример 2. Дискретная случайная величина Решение. Для дискретной случайной величины В данном случае
Пример 3. Дискретная случайная величина Решение. Обозначим третье возможное значение случайной величины через
Пример 4. Плотность распределения вероятностей случайной величины
Найти параметр Решение. Значение параметра
Пример 5. Поток заявок, поступающих на телефонную станцию, представляет собой простейший поток. Математическое ожидание числа вызовов за час равно 30. Найти вероятность того, что за минуту поступит не менее двух вызовов. Решение. Так как поток заявок представляет собой простейший поток, то число заявок, поступающих на телефонную станцию, распределено по закону Пуассона
с математическим ожиданием Следовательно, для решаемой задачи Обозначим через
= Пример 6. Случайная величина Найти вероятность Решение. Известно, что математическое ожидание и дисперсия пуассоновского распределения совпадают и равны значению его пара-метра
решениями которого являются числа
Для искомой вероятности получаем
Известно, что Пример 7. Время безотказной работы некоторого узла сложного агрегата – экспоненциальная случайная величина со средним Решение. По условию задачи
Известно, что математическое ожидание экспоненциальной случайной величины есть величина, обратная параметру:
Таким образом, вероятность отказа узла в течение 10 часов будет равна Если запараллелено
Искомое значение
IV. ТЕОРИЯ ВЕРОЯТНОСТИ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 821; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.164.231 (0.013 с.) |

 , состоящее из
, состоящее из 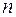 элементов. Существуют два принципиально различных способа выбора элементов из множества
элементов. Существуют два принципиально различных способа выбора элементов из множества  вычисляется по формуле
вычисляется по формуле .
. называется любой упорядоченный набор из
называется любой упорядоченный набор из  .
. вычисляется по формуле
вычисляется по формуле .
.

 из трёх элементов. Тогда все размещения двух элементов из трёх таковы:
из трёх элементов. Тогда все размещения двух элементов из трёх таковы:  Все перестановки множества
Все перестановки множества  имеют вид:
имеют вид:  и
и  Все сочетания двух элементов из множества
Все сочетания двух элементов из множества 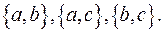
 .
.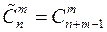 .
. элементов первого типа,
элементов первого типа,  элементов второго типа, …,
элементов второго типа, …,  элементов
элементов  го типа
го типа  , то число перестановок с повторениями вычисляется по формуле
, то число перестановок с повторениями вычисляется по формуле  .
. Правило суммы: если объект
Правило суммы: если объект  может быть выбран
может быть выбран  может быть выбран
может быть выбран  способами.
способами. способами.
способами. групп элементов, причем
групп элементов, причем  -я группа состоит из
-я группа состоит из  – элементов. Выберем по одному элементу из каждой группы, тогда общее число
– элементов. Выберем по одному элементу из каждой группы, тогда общее число  способов, которыми можно произвести такой выбор по правилу произведения
способов, которыми можно произвести такой выбор по правилу произведения . (1)
. (1)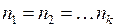 , то можно считать, что выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда
, то можно считать, что выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда  .
. Второй и третий делают то же самое,
Второй и третий делают то же самое,  Согласно формуле (1), общее число способов будет равно
Согласно формуле (1), общее число способов будет равно  Подсчитаем число благоприятных исходов. Для этого сначала найдем общее число комбинаций задуманных чисел, в которых нет совпадений. Первый студент может выбрать любое из 10 чисел, второй любое из 9 чисел, а третий студент – любое из оставшихся 8 чисел. Поэтому общее число комбинаций задуманных чисел, в которых нет совпадений, по формуле (1) равно
Подсчитаем число благоприятных исходов. Для этого сначала найдем общее число комбинаций задуманных чисел, в которых нет совпадений. Первый студент может выбрать любое из 10 чисел, второй любое из 9 чисел, а третий студент – любое из оставшихся 8 чисел. Поэтому общее число комбинаций задуманных чисел, в которых нет совпадений, по формуле (1) равно  Остальные случаи (1000 – 720 =280) характеризуются наличием хотя бы одного совпадения. Следовательно, искомая вероятность равна
Остальные случаи (1000 – 720 =280) характеризуются наличием хотя бы одного совпадения. Следовательно, искомая вероятность равна 
 . Из этих исходов благоприятными появлению события {появится последовательность букв, которая начинается словом «мир»} будут все исходы, в которых на первых трех позициях будет стоять слово «мир» (такому выбору соответствует один исход), а остальные позиции будут заполнены любым образом (число таких вариантов
. Из этих исходов благоприятными появлению события {появится последовательность букв, которая начинается словом «мир»} будут все исходы, в которых на первых трех позициях будет стоять слово «мир» (такому выбору соответствует один исход), а остальные позиции будут заполнены любым образом (число таких вариантов  ). По правилу произведения число благоприятных исходов
). По правилу произведения число благоприятных исходов  .
. .
. .
. } будут те исходы, в которых элементы (шары) не будут повторяться. Число таких исходов – это число размещений из трех элементов по три, или число перестановок из трех элементов, то есть
} будут те исходы, в которых элементы (шары) не будут повторяться. Число таких исходов – это число размещений из трех элементов по три, или число перестановок из трех элементов, то есть  . Так как все исходы опыта равновозможные, то
. Так как все исходы опыта равновозможные, то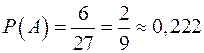 .
. , то есть
, то есть 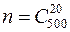 .
. ={среди проверяемых деталей будет ровно две нестандартные} (следовательно, остальные 18 должны быть стандартными), будет соответствовать (правило произведения)
={среди проверяемых деталей будет ровно две нестандартные} (следовательно, остальные 18 должны быть стандартными), будет соответствовать (правило произведения)  исходов, то есть
исходов, то есть  . Таким образом,
. Таким образом, .
. .
. 
 так как число десятков и единиц может произвольно меняться от 1 до 6. Такие же рассуждения справедливы, если число сотен равно 6. Опытов, у которых первые две цифры 45 будет 6. Используя правила произведения и суммы, найдем количество таких чисел
так как число десятков и единиц может произвольно меняться от 1 до 6. Такие же рассуждения справедливы, если число сотен равно 6. Опытов, у которых первые две цифры 45 будет 6. Используя правила произведения и суммы, найдем количество таких чисел 
 . Так как все исходы опыта равновозможные, то искомая вероятность
. Так как все исходы опыта равновозможные, то искомая вероятность 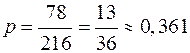 .
.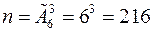 . Благоприятными событию A ={по крайней мере, две радиостанции будут работать на одинаковых частотах} будут те исходы, в которых элементы (частоты) будут повторяться. Число таких исходов –
. Благоприятными событию A ={по крайней мере, две радиостанции будут работать на одинаковых частотах} будут те исходы, в которых элементы (частоты) будут повторяться. Число таких исходов –  и три радиостанции работают на одной частоте –
и три радиостанции работают на одной частоте –  . Число исходов, в которых две из трех радиостанций могут работать на одной из шести частот, – это
. Число исходов, в которых две из трех радиостанций могут работать на одной из шести частот, – это 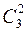 . Число различных частот – 6. Третья радиостанция может работать на одной из пяти «незанятых» частот. По правилу произведения
. Число различных частот – 6. Третья радиостанция может работать на одной из пяти «незанятых» частот. По правилу произведения  . Очевидно, что число исходов
. Очевидно, что число исходов  .
.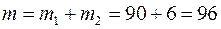 .
.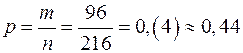 .
.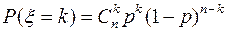
 ,
, 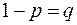 ,
,  ,
, ,
,  .
.
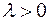 ,
,  ,
,  ,
,  .
.
 ,
,  .
. )
) ,
,  ,
,  ,
,  ,
, 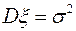 .
. означает, что случайная величина
означает, что случайная величина  распределена нормально с параметрами
распределена нормально с параметрами  .
.
 ,
, 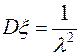 .
.
 ,
, 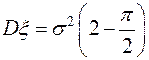 .
. ,
, 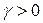


 – гамма-функция:
– гамма-функция: 

 ).
). , б)
, б)  , в)
, в)  .
. число изделий, прошедших испытания. Очевидно, что случайная величина
число изделий, прошедших испытания. Очевидно, что случайная величина 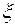 может принимать значения от 1 и, теоретически, до бесконечности.
может принимать значения от 1 и, теоретически, до бесконечности. , если осуществится событие, состоящее в том, что
, если осуществится событие, состоящее в том, что  изделия пройдут испытания, а
изделия пройдут испытания, а  – вероятность того, что изделие пройдет испытание, а
– вероятность того, что изделие пройдет испытание, а  – вероятность того, что изделие не пройдет испытание, то по теореме умножения вероятностей случайных событий,
– вероятность того, что изделие не пройдет испытание, то по теореме умножения вероятностей случайных событий, 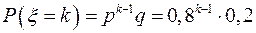 , где
, где  .
.
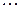




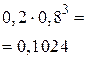
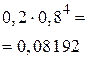
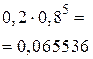

 и соединим их ломаной.
и соединим их ломаной.




 .
. ,
,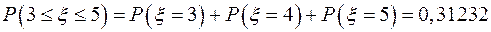 .
. ,
, 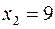 ,
,  . Вероятности этих значений соответственно равны
. Вероятности этих значений соответственно равны  ,
,  ,
,  . Найти математическое ожидание
. Найти математическое ожидание  , дисперсию
, дисперсию  и среднее квадратическое отклонение
и среднее квадратическое отклонение 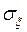 .
.
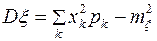 .
.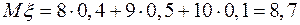 .
.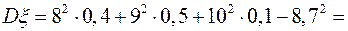
 .
. .
. . Вероятности этих значений соответственно равны
. Вероятности этих значений соответственно равны  . Найти закон распределения случайной величины
. Найти закон распределения случайной величины  .
. . Так как для дискретной случайной величины
. Так как для дискретной случайной величины  , то
, то 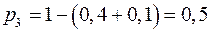 . Значение
. Значение  , то есть из уравнения
, то есть из уравнения  . Решив уравнение, найдем
. Решив уравнение, найдем  . Составим закон распределения
. Составим закон распределения


 , функцию распределения вероятностей случайной величины
, функцию распределения вероятностей случайной величины  ,
,  ,
,  .
.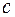 найдем из условия нормировки
найдем из условия нормировки  . Для заданной
. Для заданной  это условие примет вид
это условие примет вид  . Интегрируя, получим
. Интегрируя, получим  , откуда
, откуда  . Следовательно
. Следовательно 
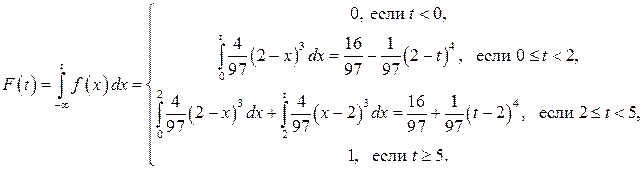
 .
. .
. .
.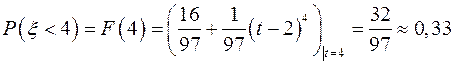 .
.
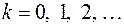 ,
,  ,
, .
.
 событие, состоящее в том, что за минуту поступит не менее двух вызовов. Тогда
событие, состоящее в том, что за минуту поступит не менее двух вызовов. Тогда

 =
=
 .
. имеет пуассоновское распределение и известно, что ее математическое ожидание
имеет пуассоновское распределение и известно, что ее математическое ожидание 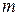 и дисперсия
и дисперсия 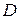 связаны соотношением
связаны соотношением  .
. ,
,  .
. . Условие задачи приводит к уравнению относительно
. Условие задачи приводит к уравнению относительно  ,
, ,
,  . Последнее значение не может быть параметром пуассоновского распределения в силу положительности параметра. Таким образом, случайная величина
. Последнее значение не может быть параметром пуассоновского распределения в силу положительности параметра. Таким образом, случайная величина  ,
,  .
.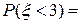





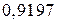 .
. . Из этого равенства
. Из этого равенства  . Для заданной случайной величины
. Для заданной случайной величины  ,
,  . Следовательно,
. Следовательно,  .
. . Для увеличения надежности агрегата узел дублируется – ставят параллельно несколько одинаковых, но функционирующих независимо узлов. Сколько узлов следует запараллелить, чтобы с вероятностью, не меньшей чем 0,9, по крайней мере один из них не вышел из строя за 10 часов работы?
. Для увеличения надежности агрегата узел дублируется – ставят параллельно несколько одинаковых, но функционирующих независимо узлов. Сколько узлов следует запараллелить, чтобы с вероятностью, не меньшей чем 0,9, по крайней мере один из них не вышел из строя за 10 часов работы?

 . По условию задачи
. По условию задачи  , следовательно,
, следовательно,  .
.

 .
. идентичных узлов, то событие
идентичных узлов, то событие  {по крайней мере один из узлов не выйдет из строя за 10 часов} является противоположным событию
{по крайней мере один из узлов не выйдет из строя за 10 часов} является противоположным событию 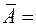 {все узлы выйдут из строя за 10 часов}. Поэтому,
{все узлы выйдут из строя за 10 часов}. Поэтому,  . Узлы работают независимо, поэтому по теореме умножения вероятностей независимых событий
. Узлы работают независимо, поэтому по теореме умножения вероятностей независимых событий .
.



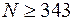 .
.


