
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы распределения дискретных случайных величин.Содержание книги Поиск на нашем сайте
Биномиальное распределение Говорят, что дискретная случайная величина X распределена по биномиальному закону, если возможные значения этой случайной величины 0, 1, 2,…, n, а вероятность каждого из значений определяется по формуле Бернулли
где 0 £ p £ 1; q = 1 – p; m = 0, 1, 2,…, n. Постоянные p и n, входящие в формулу (21), называются параметрами биномиального распределения. На практике биномиальное распределения возникает при следующих условиях: пусть производится серия из n независимых испытаний, в каждом из которых событие A может осуществиться с вероятностью p. Тогда случайная величина X, определяющая число появлений события A в серии из n испытаний, распределена по биномиальному закону. Биномиальное распределение широко используется при выборочном методе контроля продукции, т.к. определяет вероятность извлечения из партии продукции заданного количества бракованных изделий при известной доле брака. Закон называется «биномиальным» потому, что правую часть равенства (21) можно рассматривать как общий член разложения бинома Ньютона:
Ряд распределения случайной величины X, распределенной по биномиальному закону, имеет вид:
Для случайной величины, распределенной по биномиальному закону,
M [ X ] = np, D [ X ] = npq,
Пример 13 По каналу связи передается 5 сообщений. Каждое сообщение с вероятностью 0,1 независимо от других искажается. Случайная величина X – число искаженных сообщений. Построить ряд распределения этой случайной величины, вычислить ее математическое ожидание, дисперсию и среднее квадратическое отклонение непосредственно по ряду распределения и сравнить со значениями, которые получаются при использовании формул (23). Найти вероятность того, что будет искажено не более одного сообщения. Решение. Условие задачи соответствует проведению n = 5 независимых испытаний, в каждом из которых с вероятностью p = 0,1 может осуществиться событие A = {искажение передаваемого сигнала}. Случайная величина X, обозначающая число искаженных сообщений, распределена по биномиальному закону. Возможные значения этой случайной величины: 0, 1, 2, 3, 4, 5. Вероятности возможных значений случайной величины определяются по формуле Бернулли:
Ряд распределения имеет вид:
Убедимся, что Вычислим числовые характеристики данной случайной величины:
xmod = 0 [ сообщений ].
Вычислим числовые характеристики этой случайной величины по формулам (23): M [ X ] = n p = 5 × 0,1 = 0,5; D [ X ] = n p q = 5 × 0,1 × 0,9 = 0,45.
Как и следовало ожидать, получены точно такие же значения. Вероятность того, что будет искажено не более одного сообщения, P (X £ 1) = P (X = 0) + P (X = 1) = 0,59049 + 0,32805 = 0,91854.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 290; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.76.230 (0.009 с.) |

 , (21)
, (21) . (22)
. (22) . (23)
. (23)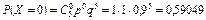 ;
;  ;
; ;
; 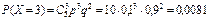 ;
; ;
;  .
.

 .
.
 ;
; [ сообщений ];
[ сообщений ];


