
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 36: Проверка гипотез о математических ожиданияхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Основная гипотеза имеет вид
Решение:
2. Наблюдаемое значение критерия проверки гипотезы
Решение:
3. Наблюдаемое значение критерия проверки гипотезы
Решение:
Кейс 1 подзадача 1 1. Курсовая стоимость ценной бумаги равна 1000 рублей. Она может в течение недели подорожать на 4 % с вероятностью 0,9 или подешеветь на 4 % с вероятностью 0,1. Предполагается, что еженедельные изменения цен независимы. Прошло две недели. Установите соответствие между случайными событиями и вероятностями этих событий. 0,19 0,81 0,01 0,18 Решение: 2. Курсовая стоимость ценной бумаги равна 1000 рублей. Она может в течение недели подорожать на 6 % с вероятностью 0,75 или подешеветь на 6 % с вероятностью 0,25. Предполагается, что еженедельные изменения цен независимы. Прошло две недели. Установите соответствие между случайными событиями и вероятностями этих событий. 0,4375 0,5625 0,0625 0,375 Решение:
3. Курсовая стоимость ценной бумаги равна 1000 рублей. Она может в течение недели подорожать на 5 % с вероятностью 0,8 или подешеветь на 5 % с вероятностью 0,2. Предполагается, что еженедельные изменения цен независимы. Прошло две недели. Установите соответствие между случайными событиями и вероятностями этих событий. 0,36 0,64 0,04 0,32 Решение:
4. Курсовая стоимость ценной бумаги равна 1000 рублей. Она может в течение недели подорожать на 2 % с вероятностью 0,6 или подешеветь на 2 % с вероятностью 0,4. Предполагается, что еженедельные изменения цен независимы. Прошло две недели. Установите соответствие между случайными событиями и вероятностями этих событий. 0,64 0,36 0,16 0,24 Решение:
Кейс 1 подзадача 2 1. Курсовая стоимость ценной бумаги равна 1000 рублей. Она может в течение недели подорожать на 4 % с вероятностью 0,9 или подешеветь на 4 % с вероятностью 0,1. Предполагается, что еженедельные изменения цен независимы. Прошло две недели. Максимально возможный курс ценной бумаги будет принадлежать интервалам (в руб.) … (1081,5; 1082,5) (1081,0; 1082,0) (1080,5; 1081,5) (1080,0; 1081,0) Решение:
2. Курсовая стоимость ценной бумаги равна 1000 рублей. Она может в течение недели подорожать на 6 % с вероятностью 0,75 или подешеветь на 6 % с вероятностью 0,25. Предполагается, что еженедельные изменения цен независимы. Прошло две недели. Максимально возможный курс ценной бумаги будет принадлежать интервалам (в руб.) … (1123,5; 1127,5) (1121,5; 1125,0) (1118,5; 1122,5) (1115,5; 1121,0) Решение:
3. Курсовая стоимость ценной бумаги равна 1000 рублей. Она может в течение недели подорожать на 5 % с вероятностью 0,8 или подешеветь на 5 % с вероятностью 0,2. Предполагается, что еженедельные изменения цен независимы. Прошло две недели. Максимально возможный курс ценной бумаги будет принадлежать интервалам (в руб.) … (1101,0; 1103,4) (1100,4; 1103,0) (1099,9; 1102,4) (1099,4; 1102,0) Решение:
4. Курсовая стоимость ценной бумаги равна 1000 рублей. Она может в течение недели подорожать на 2 % с вероятностью 0,6 или подешеветь на 2 % с вероятностью 0,4. Предполагается, что еженедельные изменения цен независимы. Прошло две недели. Максимально возможный курс ценной бумаги будет принадлежать интервалам (в руб.) … (1040,0; 1041,0) (1039,5; 1040,5) (1039,0; 1040,0) (1038,5; 1039,5) Решение:
Кейс 1 подзадача 3 1. Курсовая стоимость ценной бумаги равна 1000 рублей. Она может в течение недели подорожать на 4 % с вероятностью 0,9 или подешеветь на 4 % с вероятностью 0,1. Предполагается, что еженедельные изменения цен независимы. Прошло две недели. Математическое ожидание курсовой стоимости ценой бумаги будет равно … 1065,024 1065,00 1064,976 1000,00 Решение:
2. Курсовая стоимость ценной бумаги равна 1000 рублей. Она может в течение недели подорожать на 6 % с вероятностью 0,75 или подешеветь на 6 % с вероятностью 0,25. Предполагается, что еженедельные изменения цен независимы. Прошло две недели. Математическое ожидание курсовой стоимости ценой бумаги будет равно … 1060,90 1060,00 1059,10 1000,00 Решение:
3. Курсовая стоимость ценной бумаги равна 1000 рублей. Она может в течение недели подорожать на 5 % с вероятностью 0,8 или подешеветь на 5 % с вероятностью 0,2. Предполагается, что еженедельные изменения цен независимы. Прошло две недели. Математическое ожидание курсовой стоимости ценой бумаги будет равно … 1060,90 1050,00 1059,10 1000,00 Решение:
4. Курсовая стоимость ценной бумаги равна 1000 рублей. Она может в течение недели подорожать на 2 % с вероятностью 0,6 или подешеветь на 2 % с вероятностью 0,4. Предполагается, что еженедельные изменения цен независимы. Прошло две недели. Математическое ожидание курсовой стоимости ценой бумаги будет равно … 1008,016 1008,00 1007,944 1000,00 Решение:
Кейс 2 подзадача 1 1. Кредитный отдел банка проанализировал выданные кредиты по двум параметрам (в % от общего числа кредитов): по величине и срокам. Вероятность того, что кредит краткосрочный, если он «средний», можно оценить как …
Решение:
2. Кредитный отдел банка проанализировал выданные кредиты по двум параметрам (в % от общего числа кредитов): по величине и срокам. Вероятность того, что кредит краткосрочный, если он «крупный», можно оценить как …
Решение:
3. Кредитный отдел банка проанализировал выданные кредиты по двум параметрам (в % от общего числа кредитов): по величине и срокам. Вероятность того, что кредит долгосрочный, если он «мелкий», можно оценить как …
Решение:
Кейс 2 подзадача 2 1. Кредитный отдел банка проанализировал выданные кредиты по двум параметрам (в % от общего числа кредитов): по величине и срокам. Выдан долгосрочный кредит. Установите соответствие между видом кредита и вероятностью его выдачи. 1. «Крупный»
Решение:
2. Кредитный отдел банка проанализировал выданные кредиты по двум параметрам (в % от общего числа кредитов): по величине и срокам. Выдан краткосрочный кредит. Установите соответствие между видом кредита и вероятностью его выдачи. 1. «Крупный»
Решение:
3. Кредитный отдел банка проанализировал выданные кредиты по двум параметрам (в % от общего числа кредитов): по величине и срокам. Выдан краткосрочный кредит. Установите соответствие между видом кредита и вероятностью его выдачи. 1. «Крупный»
Решение:
Кейс 2 подзадача 3 1. Кредитный отдел банка проанализировал выданные кредиты по двум параметрам (в % от общего числа кредитов): по величине и срокам. В рассматриваемом периоде банк выдал 100 кредитов. Если средний размер кредита «Мелкий» был равен 100 тыс. руб., кредита «Средний» – 700 тыс. руб., кредита «Крупный» – 2 млн руб., то объем кредитного портфеля банка составит ____ млн руб. Решение:
2. Кредитный отдел банка проанализировал выданные кредиты по двум параметрам (в % от общего числа кредитов): по величине и срокам. В рассматриваемом периоде банк выдал 100 кредитов. Если средний размер кредита «Мелкий» был равен 100 тыс. руб., кредита «Средний» – 400 тыс. руб., кредита «Крупный» – 2 млн руб., то объем кредитного портфеля банка составит ____ млн руб. Решение:
3. Кредитный отдел банка проанализировал выданные кредиты по двум параметрам (в % от общего числа кредитов): по величине и срокам. В рассматриваемом периоде банк выдал 100 кредитов. Если средний размер кредита «Мелкий» был равен 100 тыс. руб., кредита «Средний» – 600 тыс. руб., кредита «Крупный» – 2 млн руб., то объем кредитного портфеля банка составит ____ млн руб. Решение:
Кейс 3 подзадача 1 1. Компания рассматривает проект по строительству трех домов, по одному в разных районах города. Средства для строительства дают сами будущие жильцы. Вероятность набрать необходимые средства для постройки одного дома составляет 0,6. Каждый построенный дом окупает 80 % всех затрат компании по проекту, равных 500 млн руб. Предположим, что собранных средств будет достаточно для строительства k домов. Установите соответствие между значениями k и вероятностями соответствующих случайных событий. 1. k = 1 0,288 0,432 0,216 0,6 0,36 Решение:
2. Компания рассматривает проект по строительству трех домов, по одному в разных районах города. Средства для строительства дают сами будущие жильцы. Вероятность набрать необходимые средства для постройки одного дома составляет 0,9. Каждый построенный дом окупает 50 % всех затрат компании по проекту, равных 500 млн руб. Предположим, что собранных средств будет достаточно для строительства k домов. Установите соответствие между значениями k и вероятностями соответствующих случайных событий. 1. k = 1 0,027 0,243 0,729 0,9 0,81 Решение:
3. Компания рассматривает проект по строительству трех домов, по одному в разных районах города. Средства для строительства дают сами будущие жильцы. Вероятность набрать необходимые средства для постройки одного дома составляет 0,8. Каждый построенный дом окупает 60 % всех затрат компании по проекту, равных 500 млн руб. Предположим, что собранных средств будет достаточно для строительства k домов. Установите соответствие между значениями k и вероятностями соответствующих случайных событий. 1. k = 1 0,096 0,384 0,512 0,8 0,64 Решение:
4. Компания рассматривает проект по строительству трех домов, по одному в разных районах города. Средства для строительства дают сами будущие жильцы. Вероятность набрать необходимые средства для постройки одного дома составляет 0,7. Каждый построенный дом окупает 70 % всех затрат компании по проекту, равных 500 млн руб. Предположим, что собранных средств будет достаточно для строительства k домов. Установите соответствие между значениями k и вероятностями соответствующих случайных событий. 1. k = 1 0,189 0,441 0,343 0,7 0,49 Решение:
Кейс 3 подзадача 2 1. Компания рассматривает проект по строительству трех домов, по одному в разных районах города. Средства для строительства дают сами будущие жильцы. Вероятность набрать необходимые средства для постройки одного дома составляет 0,6. Каждый построенный дом окупает 80 % всех затрат компании по проекту, равных 500 млн руб. Если обозначить через
Решение:
2. Компания рассматривает проект по строительству трех домов, по одному в разных районах города. Средства для строительства дают сами будущие жильцы. Вероятность набрать необходимые средства для постройки одного дома составляет 0,9. Каждый построенный дом окупает 50 % всех затрат компании по проекту, равных 500 млн руб. Если обозначить через
Решение:
3. Компания рассматривает проект по строительству трех домов, по одному в разных районах города. Средства для строительства дают сами будущие жильцы. Вероятность набрать необходимые средства для постройки одного дома составляет 0,8. Каждый построенный дом окупает 60 % всех затрат компании по проекту, равных 500 млн руб. Если обозначить через
Решение:
4. Компания рассматривает проект по строительству трех домов, по одному в разных районах города. Средства для строительства дают сами будущие жильцы. Вероятность набрать необходимые средства для постройки одного дома составляет 0,7. Каждый построенный дом окупает 70 % всех затрат компании по проекту, равных 500 млн руб. Если обозначить через
Решение:
Кейс 3 подзадача 3 1. Компания рассматривает проект по строительству трех домов, по одному в разных районах города. Средства для строительства дают сами будущие жильцы. Вероятность набрать необходимые средства для постройки одного дома составляет 0,6. Каждый построенный дом окупает 80 % всех затрат компании по проекту, равных 500 млн руб. Ожидаемая прибыль компании равна ____ млн руб. Решение:
2. Компания рассматривает проект по строительству трех домов, по одному в разных районах города. Средства для строительства дают сами будущие жильцы. Вероятность набрать необходимые средства для постройки одного дома составляет 0,9. Каждый построенный дом окупает 50 % всех затрат компании по проекту, равных 500 млн руб. Ожидаемая прибыль компании равна ____ млн руб. Решение: 3. Компания рассматривает проект по строительству трех домов, по одному в разных районах города. Средства для строительства дают сами будущие жильцы. Вероятность набрать необходимые средства для постройки одного дома составляет 0,8. Каждый построенный дом окупает 60 % всех затрат компании по проекту, равных 500 млн руб. Ожидаемая прибыль компании равна ____ млн руб. Решение:
4. Компания рассматривает проект по строительству трех домов, по одному в разных районах города. Средства для строительства дают сами будущие жильцы. Вероятность набрать необходимые средства для постройки одного дома составляет 0,7. Каждый построенный дом окупает 70 % всех затрат компании по проекту, равных 500 млн руб. Средняя ожидаемая прибыль компании равна ____ млн руб. Решение:
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 460; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.125.86 (0.011 с.) |

 Тогда конкурирующей может являться гипотеза …
Тогда конкурирующей может являться гипотеза …

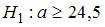
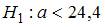
 противоречит
противоречит 
 о равенстве средних двух нормальных генеральных совокупностей с известными дисперсиями
о равенстве средних двух нормальных генеральных совокупностей с известными дисперсиями 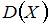 и
и  может иметь вид …
может иметь вид …



 который имеет стандартное нормальное распределение. Тогда наблюдаемое значение критерия определяется как
который имеет стандартное нормальное распределение. Тогда наблюдаемое значение критерия определяется как  где
где  и
и  – объемы независимых выборок, по которым вычислены выборочные средние
– объемы независимых выборок, по которым вычислены выборочные средние 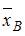 и
и  соответственно. Следовательно, например, при
соответственно. Следовательно, например, при  ,
,  получаем
получаем 

 который имеет стандартное нормальное распределение. Тогда наблюдаемое значение критерия определяется как
который имеет стандартное нормальное распределение. Тогда наблюдаемое значение критерия определяется как 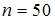 ,
,  получаем
получаем 
 заключается в том, что стоимость ценной бумаги в течение недели вырастет на 4 % до
заключается в том, что стоимость ценной бумаги в течение недели вырастет на 4 % до  руб., а событие
руб., а событие  заключается в том, что стоимость ценной бумаги в течение недели упадет на 4 % до
заключается в том, что стоимость ценной бумаги в течение недели упадет на 4 % до  руб. Следовательно,
руб. Следовательно, то есть равна
то есть равна  так как
так как 
 то есть равна
то есть равна 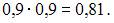
 руб., а событие
руб., а событие  руб. Следовательно,
руб. Следовательно,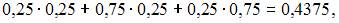 так как
так как 

 руб., а событие
руб., а событие  руб. Следовательно,
руб. Следовательно, так как
так как 

 руб., а событие
руб., а событие  руб. Следовательно,
руб. Следовательно, так как
так как 
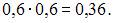
 руб. Тогда из предложенных ответов правильными будут ответы: (1081,5; 1082,5) и (1081,0; 1082,0).
руб. Тогда из предложенных ответов правильными будут ответы: (1081,5; 1082,5) и (1081,0; 1082,0). руб. Тогда из предложенных ответов правильными будут ответы: (1123,5; 1127,5) и (1121,5; 1125,0).
руб. Тогда из предложенных ответов правильными будут ответы: (1123,5; 1127,5) и (1121,5; 1125,0). руб. Тогда из предложенных ответов правильными будут ответы: (1101,0; 1103,4) и (1100,4; 1103,0).
руб. Тогда из предложенных ответов правильными будут ответы: (1101,0; 1103,4) и (1100,4; 1103,0). руб. Тогда из предложенных ответов правильными будут ответы:
руб. Тогда из предложенных ответов правильными будут ответы: – курсовой стоимости ценной бумаги, как
– курсовой стоимости ценной бумаги, как
 а
а 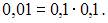


 а
а 


 а
а 


 а
а 












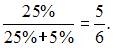



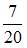


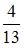





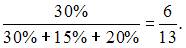








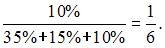


 млн руб.
млн руб. тыс. руб., или 76 млн. руб.
тыс. руб., или 76 млн. руб.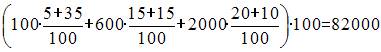 тыс. руб., или 82 млн руб.
тыс. руб., или 82 млн руб. где
где 

 Тогда:
Тогда:
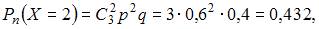


 Тогда:
Тогда:



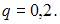 Тогда:
Тогда:



 Тогда:
Тогда:






 млн руб., то прибыль компании можно определить как
млн руб., то прибыль компании можно определить как 



 млн руб., то прибыль компании можно определить как
млн руб., то прибыль компании можно определить как 



 млн руб., то прибыль компании можно определить как
млн руб., то прибыль компании можно определить как 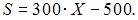

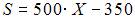

 млн руб., то прибыль компании можно определить как
млн руб., то прибыль компании можно определить как 

 млн руб.
млн руб.
 млн руб.
млн руб.
 млн руб.
млн руб.
 млн руб.
млн руб.


