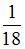Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 7: Числовые характеристики дискретных случайных величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Дискретная случайная величина X задана законом распределения вероятностей: 0,80 0,64 2,60 14,16 Решение:
2. Дискретная случайная величина X задана законом распределения вероятностей:
Решение:
Тема 8: Биномиальный закон распределения вероятностей 1. Проводится n независимых испытаний, в каждом из которых вероятность появления события A постоянна и равна 0,6. Тогда математическое ожидание
Решение: 2. Проводится n независимых испытаний, в каждом из которых вероятность появления события A постоянна и равна
Решение: 4. В среднем 80% студентов группы сдают зачет с первого раза. Тогда вероятность того, что из 6 человек, сдававших зачет, с первого раза сдадут ровно 4 студента, равна …
Решение: Тема 9: Простейший поток событий. Распределение Пуассона 1. Среднее число заявок, поступающих на предприятие бытового обслуживания за 1 час равно пяти. Тогда вероятность того, что за два часа поступит восемь заявок, можно вычислить как …
Решение:
3. Среднее число заявок, поступающих на предприятие бытового обслуживания за 1 час, равно трем. Тогда вероятность того, что за два часа поступит пять заявок, можно вычислить как …
Решение: Тема 10: Вероятности состояний цепи Маркова 1. Матрица вероятностей перехода однородной цепи Маркова имеет вид
Решение:
2. Матрица вероятностей перехода однородной цепи Маркова имеет вид
Решение:
3. Матрица вероятностей перехода однородной цепи Маркова имеет вид
Решение:
Тема 11: Плотность распределения вероятностей непрерывной случайной величины 1. Непрерывная случайная величина
Решение:
2. Непрерывная случайная величина
Решение:
3. Непрерывная случайная величина
Решение:
4. Непрерывная случайная величина
Решение:
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 717; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.104.175 (0.009 с.) |


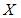 определяется как
определяется как  где дисперсию
где дисперсию 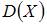 дискретной случайной величины можно вычислить по формуле
дискретной случайной величины можно вычислить по формуле 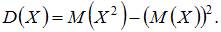 Тогда
Тогда 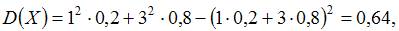 а
а 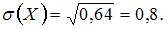




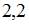
 . Тогда
. Тогда 
 и дисперсия
и дисперсия 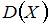 дискретной случайной величины X – числа появлений события A в
дискретной случайной величины X – числа появлений события A в  проведенных испытаниях – равны …
проведенных испытаниях – равны …


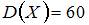


 а
а 
 . Тогда математическое ожидание
. Тогда математическое ожидание  проведенных испытаниях – равны …
проведенных испытаниях – равны …


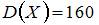


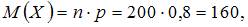 а
а 
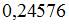


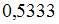
 где
где 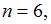


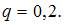


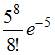


 событий простейшего потока за время
событий простейшего потока за время  определяется формулой Пуассона:
определяется формулой Пуассона: где
где  – интенсивность потока.
– интенсивность потока. ,
,  ,
, 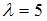 , то
, то 

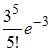


 ,
,  ,
,  , то
, то 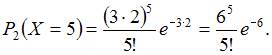
 , а вектор начального распределения вероятностей –
, а вектор начального распределения вероятностей –  . Тогда вектор вероятностей состояний цепи Маркова на втором шаге равен …
. Тогда вектор вероятностей состояний цепи Маркова на втором шаге равен …



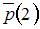 состояний цепи Маркова на втором шаге можно вычислить последовательно как
состояний цепи Маркова на втором шаге можно вычислить последовательно как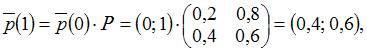
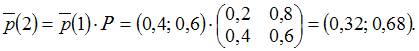
 а вектор вероятностей состояний цепи Маркова на втором шаге равен
а вектор вероятностей состояний цепи Маркова на втором шаге равен  . Тогда вектор вероятностей состояний цепи Маркова на третьем шаге равен …
. Тогда вектор вероятностей состояний цепи Маркова на третьем шаге равен …



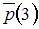 состояний цепи Маркова на третьем шаге можно вычислить как
состояний цепи Маркова на третьем шаге можно вычислить как
 а вектор начального распределения вероятностей –
а вектор начального распределения вероятностей –  . Тогда вектор вероятностей состояний цепи Маркова на втором шаге равен …
. Тогда вектор вероятностей состояний цепи Маркова на втором шаге равен …

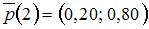


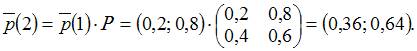

 равно …
равно …



 то
то  или
или 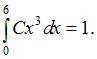 Тогда
Тогда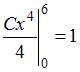 и
и 

 равна …
равна …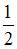

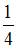
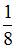
 Тогда
Тогда 
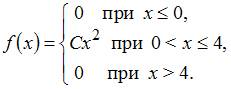

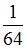


 или
или  Тогда
Тогда и
и 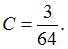

 равна …
равна …