
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 3. Теория вероятностей.Содержание книги
Поиск на нашем сайте
Случайные события. Вероятность события. Теория вероятностей- это математическая наука, которая изучает закономерности в случайных событиях. К основным понятиям теории вероятности относятся испытания и события. Под испытанием понимаю реализацию данного комплекса условий, в результате которого непременно произойдет какое либо событие. Например, бросание монеты- испытание, появление герба или цифры – события. Случайным событием называется событие, связанное с данным испытанием, которое при осуществлении испытания может произойти, а может и не произойти Слово «случайное» для краткости часто опускают и говорят просто «событие». Например, выстрел по цели - опыт, случайные события в этом опыте - попадание в цель или промах. Событие называют достоверным, если в результате опыта оно непременно должно произойти, и невозможным, если оно заведомо не произойдет. Например, выпадение не более 6 очков при бросании одной игральной кости- достоверное событие, выпадение десяти очков при бросании одной игральной кости- невозможное событие. События называются несовместимыми, если никакие два из них не могут появиться вместе. Например, попадание и промах при одном выстреле- это несовместимые события. Несколько событий в данном опыте образуют полную систему событий, если в результате опыта непременно должно произойти хотя бы одно из них. Например, при бросании игральной кости событие, состоящие в падении одного, двух, трех, четырех, пяти и шести очков, образует полную систему событий. События называются равновозможными, если ни одно из них не является объективно более возможным, чем другие. Например, при бросании монеты выпадение герба или числа- события одинаково возможные. Каждое событие обладает какой то степенью возможности. Численная мера степени объективной возможности события- это вероятность события. Вероятность события А обозначается Р(А). Пусть из системы n несовместимых равновозможных исходов испытания m исходов благоприятствуют событию А. Тогда вероятность события А называют отношение mчисла исходов, благоприятствующих событию А, к числу всех исходов данного испытания: P(A)= m/n Эта формула носит название классического определения вероятности. Если В- достоверное событие, то m=n и P(B)=1, то m Таким образом, вероятность события заключена в следующих приделах: 0<Р(А) Пример 1. Игральную кость подбрасывают один раз. Найти вероятность событий: А- появление четного числа очков, В- появление не менее пяти очков, С- появление не более 5 очков. Решение: Опыт имеет шесть равновозможных независимых исходов (появление одного, двух, трех, четырех, пяти и шести очков), образующих полную систему. Событию А благоприятствуют три исхода (выпадение двух, четырех и шести очков), поэтому Р(А)=3/6=1/2, событию В- два исхода (выпадение пяти и шести очков), поэтому Р(В)=2/6=1/3; событию С- ять исходов (выпадение одного, двух, трех, четырех и пяти очков), поэтому Р(С)= 5/6. При вычислении вероятности часто приходится использовать формулы комбинаторики. Основные понятия комбинаторики. Размещение. Пусть имеется множество, содержащее n элементов. Каждое его упорядоченное подмножество, содержащее m элементов, называется размещением из n элементов по m элементов. Из определения вытекает, что 0 Число размещений из n элементов по m в каждом обозначают
Число размещений из n элементов по m элементов каждом равно произведению m последовательно убывающих натуральных чисел, из которых большее есть n. Для краткости произведения первых n натуральных чисел принято обозначать n! (n- факториал): 1·2·3… n= n! Усвоились считать что 0!=1 Тогда формулу числа размещений из n элементов по m элементов можно записать в другом виде:
Пример 2. Сколькими способами собрание, состоящие из 30 человек, может выбрать из присутствующих президиум в составе председателя, секретаря и члена президиума? Решение. Состав президиума собрания является упорядоченным множеством из 30 элементов по три элемента. Значит, искомое число способов равно числу размещений из 30 элементов по три элемента в каждом:
Перестановки. Размещения из n элементов по n элементов перестановками из n элементов. Из определения следует что перестановки являются частным случаем размещений. Так как каждая перестановка содержит все n элементов множества то различные перестановки отличаются друг от друга только порядком элементов. Число перестановок из элементов данного множества обозначают Рn и вычисляют по формуле Рn=1·2·3…n=n!. ПРИМЕР 3. Сколько четырехзначных чисел можно составить из четырех цифр 1,2,3,4 без повторений? Решение. По условию дано множество из четырех элементов, которые требуется расположить в определенном порядке. Значит, требуется найти кол-во перестановок из четырех элементов: Р4=1·2·3·4=24, т.е. из цифр 1,2,3,4 можно составить 24 четырехзначных числа(без повторений цифр). Сочетание. Пусть имеется множество, состоящее из n элементов. Каждое его подмножество, содержащее m элементов, называется сочетанием из n элементов по m элементов. Таким образом сочетания из n элементов по m элементов – это все m элементные подмножества которые имеют одинаковый состав элементов. Подмножества отличающиеся друг от друга порядком следования элементов не считают различными. Число подмножеств по m элементов в каждом, содержащихся во множестве из во множестве из n элементов, т. е. число сочетаний из n элементов по m элементов в каждом, обозначают
Число сочетаний Так,= Пример 4. Сколькими способами можно распределить 12 человек по бригадам если в каждой бригаде по 6 человек? Решение. Состав каждой бригады является конечным множеством из 12 элементов по 6. Значит, искомое число способов равно числу сочетаний из12 элементов по 6 в каждом:
Примеры непосредственного вычисления вероятностей. ПРИМЕР 5. В урне находится 6 белых и 5 черных шаров. Из урны одновременно вынимают два шара. Какова вероятность того, что оба шара белые?(событие А) Решение. Здесь число равновозможных независимых исходов составляет n= Пример 6. В партии из 20 изделий четыре бракованных. Найти вероятность того, что среди пяти взятых наугад изделий окажется два бракованных (событие В). Решение. Здесь число равновозможных независимых исходов есть n = Подсчитаем число исходов m, благоприятствующих событию В. Среди пяти взятых изделий окажется два бракованных и три стандартных. Два бракованных изделия из четырех можно выбрать Раздел 4. Теория рядов Решение типового варианта контрольной работы. Пример 1. Исследовать на сходимость числовые ряды: а) б) в) г) д) е) ж) з) Решение. а) В данном случае Вычислим Следовательно, ряд расходится. б) Поскольку в записи общего члена ряда есть показательная функция Для рассматриваемого ряда
Вычислим
Следовательно, по признаку Даламбера, исходный ряд сходится. в) Так как в записи общего члена ряда есть факториал (
Вычислим
В пределе получили бесконечность, следовательно, исследуемый ряд расходится. г) Воспользуемся радикальным признаком Коши. Здесь Вычислим
Полученное значение больше 1, следовательно, ряд расходится. д) Исследуем данный ряд с помощью интегрального признака Коши. Составим соответствующий интеграл и вычислим его
Интеграл сходится, следовательно, исследуемый ряд сходится. е) Составим ряд, эквивалентный исходному, оставив в числителе и знаменателе лишь старшие степени n:
Полученный ряд эквивалентен исходному, так как
Таким образом, исходный ряд и ряд ж) Так как
Ряд з) Оценим общий член ряда:
Ряд Ряд Пример2. Найти область сходимости ряда Решение. Воспользуемся признаком Даламбера:
Ряд сходится, если
Ряд расходится, если Неопределенный случай: Пусть Ряд Пусть Этот ряд – знакочередующийся. Исследуя его на абсолютную сходимость (рассматриваем ряд, состоящий из абсолютных величин), получим ряд как и при Получили, что Контрольная работа 1.
Контрольная работа 2.
Контрольная работа 3. (в форме тестов) Вариант 1.
1) 30 2) 100 3) 120 4) 5 2. В 9«Б» классе 32 учащихся. Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде? 1) 128 2) 35960 3) 36 4)46788 3. Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными? 1) 10 2) 60 3) 20 4) 30 4. Вычислить: 6! -5! 1) 600 2) 300 3) 1 4) 1000 5. В ящике находится 45 шариков, из которых 17 белых. Потеряли 2 не белых шарика. Какова вероятность того, что выбранный наугад шарик будет белым? 1) 6. Бросают три монеты. Какова вероятность того, что выпадут два орла и одна решка? 1) 7. В денежно-вещевой лотерее на 1000000 билетов разыгрывается 1200 вещевых и 800 денежных выигрышей. Какова вероятность выигрыша? 1) 0,02 2) 0,00012 3) 0,0008 4) 0,002 Вариант 2.
1) 100 2) 30 3) 5 4) 120 2. Имеются помидоры, огурцы, лук. Сколько различных салатов можно приготовить, если в каждый салат должно входить 2 различных вида овощей? 1) 3 2) 6 3) 2 4) 1 3. Сколькими способами из 9 учебных предметов можно составить расписание учебного дня из 6 различных уроков. 1) 10000 2) 60480 3) 56 4) 39450 4. Вычислите: 1) 2 2) 56 3) 30 4) 5. В игральной колоде 36 карт. Наугад выбирается одна карта. Какова вероятность, что эта карта – туз? 1) 6. Бросают два игральных кубика. Какова вероятность того, что выпадут две четные цифры? 1) 0,25 2) 7. В корзине лежат грибы, среди которых 10% белых и 40% рыжих. Какова вероятность того, что выбранный гриб белый или рыжий? 1) 0,5 2) 0,4 3) 0,04 4) 0,8 Вариант 3.
1) 24 2) 4 3) 16 4) 20 2. Сколько диагоналей имеет выпуклый семиугольник? 1) 30 2) 21 3) 14 4) 7 3. В футбольной команде 11 человек. Необходимо выбрать капитана и его заместителя. Сколькими способами это можно сделать? 1) 22 2) 11 3) 150 4) 110 4. Сократите дробь: 1) 1 2) 5. Какова вероятность, что при одном броске игрального кубика выпадает число очков, равное четному числу? 1) 6. Катя и Аня пишут диктант. Вероятность того, что Катя допустит ошибку, составляет 60%, а вероятность ошибки у Ани составляет 40%. Найти вероятность того, что обе девочки напишут диктант без ошибок. 1) 0,25 2) 0, 4 3) 0,48 4) 0,2 7. Завод выпускает 15% продукции высшего сорта, 25% - первого сорта, 40% - второго сорта, а все остальное – брак. Найти вероятность того, что выбранное изделие не будет бракованным. 1) 0,8 2) 0,1 3) 0,015 4) 0,35 Вариант 4
1) 5 2) 120 3) 25 4) 100 2. Сколькими способами из 25 учеников класса можно выбрать четырех для участия в праздничном концерте? 1) 12650 2) 100 3) 75 4)10000 3. Сколько существует трехзначных чисел, все цифры. Которых нечетные и различные. 1) 120 2) 30 3) 50 4) 60 4. Упростите выражение: 1) 0,5 2) 5. Какова вероятность, что ребенок родится 7 числа? 1) 6. Каждый из трех стрелков стреляет в мишень по одному разу, причем попадания первого стрелка составляет 90%, второго – 80%, третьего – 70%. Найдите вероятность того, что все три стрелка попадут в мишень? 1) 0,504 2) 0,006 3) 0,5 4) 0,3 7. Из 30 учеников спорткласса, 11 занимается футболом, 6 – волейболом, 8 – бегом, а остальные прыжками в длину. Какова вероятность того, что один произвольно выбранный ученик класса занимается игровым видом спорта? 1) Вариант 5 1. Сколько существует вариантов рассаживания 6 гостей на 6 стульях? 1) 36 2) 180 3) 720 4) 300 2. Аня решила сварить компот из фруктов 2-ух видов. Сколько различных вариантов (по сочетанию фруктов) компотов может сварить Аня, если у нее имеется 7 видов фруктов? 1) 14 2) 10 3) 21 4) 30 3. Сколько существует обыкновенных дробей, числитель и знаменатель которых – простые различные числа не больше 20? 1) 80 2) 56 3) 20 4) 60 4. Упростите выражение: 1) 5. Какова вероятность того, что выбранное двузначное число делится на 12? 1) 6. Николай и Леонид выполняют контрольную работу. Вероятность ошибки при вычислениях у Николая составляет 70%, а у Леонида – 30%. Найдите вероятность того, что Леонид допустит ошибку, а Николай нет. 1) 0,21 2) 0,49 3) 0,5 4) 0,09 7. Музыкальная школа проводит набор учащихся. Вероятность быть не зачисленным во время проверки музыкального слуха составляет 40%, а чувство ритма – 10%. Какова вероятность положительного тестирования? 1) 0,5 2) 0,4 3) 0,6 4) 0,04 Вариант 6
1) 12 2) 20 3) 24 4) 4
1) 792 2) 17 3) 60 4) 300
1) 100 2) 720 3) 300 4) 60 4. Упростите выражение: 1) 5. В ящике лежат карточки с буквами, из которых можно составить слово «электрификация». Какова вероятность того, что наугад выбранная буква окажется буквой к? 1) 6. Каждый из трех стрелков стреляет в мишень по одному разу, причем вероятность попадания 1 стрелка составляет 80%, второго – 70%, третьего – 60%. Найдите вероятность того, что двое из трех стрелков попадет в мишень. 1) 0,336 2) 0,452 3) 0,224 4) 0,144 7. В корзине лежат фрукты, среди которых 30% бананов и 60% яблок. Какова вероятность того, что выбранный наугад фрукт будет бананом или яблоком? 1) 0,9 2) 0,5 3) 0,34 4) 0,18 Вариант 7 1. В корзине лежит: яблоко, апельсин, грейпфрут и манго. Сколькими способами 4 девочки могут поделить фрукты? (одной девочке один фрукт) 1) 4 2) 24 3) 20 4) 16 2. На плоскости расположены 25 точек так, что три из них не лежат на одной прямой. Сколько существует треугольников с вершинами в этих точках? 1) 75 2) 100 3) 2300 4) 3000 3. В теннисном турнире участвуют 10 спортсменов. Сколькими способами теннисисты могут завоевать золото, серебро и бронзу? 1) 600 2) 100 3) 300 4)720 4. Вычислите: 1) 1 2) 13 3) 12 4) 32 5. Случайным образом открывается учебник литературы и находится второе слово на странице. Какова вероятность того, что это слово начинается на букву л? 1) 6. Вступительный экзамен в лицей состоит из трех туров. Вероятность отсева в 1 туре составляет 60%, во втором - 40%, в третьем – 30%. Какова вероятность поступления в лицей? 1) 0,24 2) 0,12 3) 0,18 4) 0,072 7. В коробке лежат 4 голубых, 3 красных, 9 зеленых, 6 желтых шариков. Какова вероятность того, что выбранный шарик будет не зеленым? 1) Вариант 8
1) 6 2) 12 3) 30 4) 3 2. Сколько можно составить из простых делителей числа 2730 составных чисел, имеющих только два простых делителя? 1) 300 2) 10 3) 150 4) 15 3. На плоскости даны 8 точек, причем три из них не лежат на одной прямой. Сколько существует векторов с началом и концом в любых двух из данных точек? 1) 18 2) 28 3) 64 4) 56 4. Вычислите: 1) 48 2) 94 3) 56 4) 96 5. Катя забыла последнюю цифру семизначного номера телефона знакомой девочки. Какова вероятность того, что Катя набрала телефон знакомой девочки? 1) 0,5 2) 0,1 3) 6. Три выключателя соединены параллельно. Вероятность выхода из строя первого выключателя равна 3%, второго – 4%, третьего – 1%. Какова вероятность того, что цепь будет разомкнута? 1) 12 2) 0,5 3) 0,12 4) 12 ∙10 7.На экзамене по математике для усиления контроля класс из 35 учащихся рассадили в три аудитории. В первую посадили 10 человек, во вторую – 12, в третью – остальных. Какова вероятность того, что два друга окажутся в одной аудитории? 1) Вариант 9
1) 120 2) 360 3) 180 4) 500
1) 60 2) 85 3) 6188 4)6000
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1077; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.179.30 (0.009 с.) |

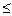 n и Р(А)
n и Р(А)  и что размещение из n элементов по m- элементные подмножества, отличающиеся составом элементов или порядком их следования.
и что размещение из n элементов по m- элементные подмножества, отличающиеся составом элементов или порядком их следования.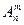 и вычисляются по формуле:
и вычисляются по формуле: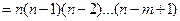

 =30·29·28=24360 или
=30·29·28=24360 или  и вычисляют по формуле:
и вычисляют по формуле: или
или 
 (0≤ m ≤n).
(0≤ m ≤n). =
=  =(10·9·8)/(1·2·3)=120
=(10·9·8)/(1·2·3)=120 =(12·11·10·9·8·7)/(1·2·3·4·5·6)=924.
=(12·11·10·9·8·7)/(1·2·3·4·5·6)=924.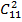 =(11·10)/(1·2)=55. Событию А благоприятствуют
=(11·10)/(1·2)=55. Событию А благоприятствуют  =(6·5)/(1·2)=15 исходов. Следовательно Р(А)=15/55=3/11.
=(6·5)/(1·2)=15 исходов. Следовательно Р(А)=15/55=3/11. =(20·19·18·17·16)/(1·2·3·4·5)=15504
=(20·19·18·17·16)/(1·2·3·4·5)=15504 =(4·3)/(1·2)=6 способами, а три стандартных изделия из 16 можно выбрать
=(4·3)/(1·2)=6 способами, а три стандартных изделия из 16 можно выбрать  =(16·15·14)/(1·2·3)=560 способами. Каждая комбинация бракованных изделий может сочетаться с каждой комбинацией стандартных изделий, поэтому m=560·6=3360. Следовательно, Р(В)=3360/15504=70/323≈0,2.
=(16·15·14)/(1·2·3)=560 способами. Каждая комбинация бракованных изделий может сочетаться с каждой комбинацией стандартных изделий, поэтому m=560·6=3360. Следовательно, Р(В)=3360/15504=70/323≈0,2.









 , то используем признак Даламбера.
, то используем признак Даламбера. ;
; 

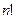 ), то используем признак Даламбера. Для исследуемого ряда
), то используем признак Даламбера. Для исследуемого ряда






 сходятся и расходятся одновременно. Т.к. ряд
сходятся и расходятся одновременно. Т.к. ряд  сходится, следовательно, исходный ряд также сходится.
сходится, следовательно, исходный ряд также сходится. , то
, то .
. расходится
расходится  , следовательно, исходный ряд также расходится.
, следовательно, исходный ряд также расходится. .
.
 сходится
сходится  , следовательно, эквивалентный ряд
, следовательно, эквивалентный ряд  также сходится. Т.к. из сходимости большего ряда следует сходимость меньшего, то исходный ряд сходится.
также сходится. Т.к. из сходимости большего ряда следует сходимость меньшего, то исходный ряд сходится. .
.

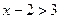 или
или 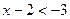 ;
; или
или  ,
, .
. .
.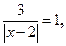 т.е.
т.е.  или
или  ,
, ‑ сходится.
‑ сходится. сходится как эквивалентный сходящемуся ряду.
сходится как эквивалентный сходящемуся ряду. :
: 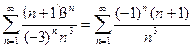 .
. ‑ область сходимости ряда.
‑ область сходимости ряда. , В =
, В = 
 , В =
, В = 
 , В =
, В = 
 , В =
, В = 
 , В =
, В = 
 , В =
, В = 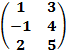
 , В =
, В = 
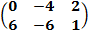 , В =
, В = 
 , В =
, В = 
 , В =
, В = 


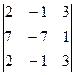


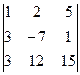



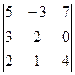

















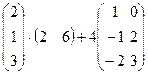
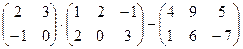


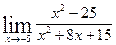

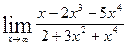
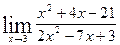



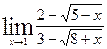

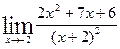
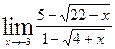





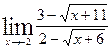








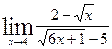







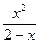
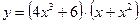








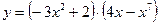



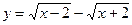




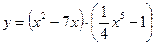





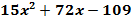


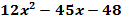













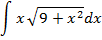

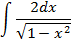














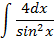

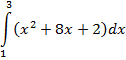



 2)
2)  3)
3)  4)
4)  2) 0,5 3) 0,125 4)
2) 0,5 3) 0,125 4) 

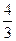
 2)
2)  3)
3) 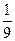 4)
4) 
 3) 0,5 4) 0,125
3) 0,5 4) 0,125
 3)
3)  4)
4) 
 2) 0,5 3)
2) 0,5 3) 
 3) n
3) n  4) n
4) n  -1
-1 2)
2)  3)
3)  4)
4) 
 2) 0,5 3)
2) 0,5 3)  4)
4) 

 2)
2)  3)
3)  4) 0
4) 0 2)
2)  3)
3)  4)
4) 

 2)
2)  3)
3)  4) 0
4) 0 2) 7 3)
2) 7 3) 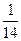 4)
4) 

 2)
2)  3)
3)  4)
4) 
 2) 0,5 3)
2) 0,5 3)  4)
4) 


 2) 0,5 3)
2) 0,5 3)  4)
4) 



