
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правило нахождения точек перегибаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
графика функции 1. Найти вторую производную 2. Найти критические точки II рода функции 3. Исследовать знак второй производной 4. Вычислить значения функции в точках перегиба.
Пример 1: Найти промежутки выпуклости и точки перегиба следующей кривой: Решение: Находим Найдем критические точки по второй производной, решив уравнение
Ответ: Функция выпукла вверх при функция выпукла вниз при точка перегиба
Общая схема для построения графиков функций
1. Найти область определения функции 2. Найти точки пересечения графика функций с осями координат. 3. Исследовать функцию на четность или нечетность. 4. Исследовать функцию на периодичность. 5. Найти промежутки монотонности и точки экстремума функции. 6. Найти промежутки выпуклости и точки перегиба функции. 7. Найти асимптоты функции. 8. По результатам исследования построить график. Пример: Исследовать функцию и построить ее график:
Решение: 1) Функция определена на всей числовой оси, т. е. ее область определения 2) Найдем точки пересечения с осями координат: с осью ОХ: решим уравнение
с осью ОY: 3) Выясним, не является ли функция четной или нечет ной:
Отсюда следует, что функция является нечетной. 4) Функция непериодична. 5) Найдем промежутки монотонности и точки экстремума функции: Критические точки:
6) Найдем промежутки выпуклости и точки перегиба функции: Критические точки:
7) Функция непрерывна, асимптот у нее нет. 8) По результатам исследования построим график функции:
1 x -2
Тема 2.3. Интегральное исчисление. Неопределенный интеграл. Методы вычисления
Определение: Функция F(x) называется первообразной для функции f(x), если Любая непрерывная функция f(x) имеет бесконечное множество первообразных, которые отличаются друг от друга постоянным слагаемым. Определение: Совокупность F(x)+С всех первообразных для функции f(x) называется неопределенным интегралом от этой функции и обозначается:
Основные свойства неопределенного интеграла: 1. 3. 5. Таблица интегралов
Рассмотрим нахождение интегралов непосредственным методом.
Пример 1: Найти неопределенный интеграл:
Решение: =
Пример 2: Найти неопределенный интеграл: Решение:
Пример 3: Найти неопределенный интеграл Решение:
Метод подстановки в неопределенном интеграле (метод замены переменной) Этот метод заключается в том, что заменяют переменную х на При этом получают искомую функцию, выраженную через переменную t. Для возвращения к переменной х необходимо заменить t значением Рассмотрим нахождение интегралов методом подстановки.
Пример 1: Найти неопределенный интеграл Решение:
Пример 2: Найти неопределенный интеграл Решение: = Пример 3: Найти неопределенный интеграл Решение: Пример 4: Найти неопределенный интеграл Решение: = Определенный интеграл и его свойства Пусть функция Интегральной суммой для функции
Определение: Определенным интегралом от функции
Для любой функции
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 745; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.52.29 (0.01 с.) |


 .
. . Если при этом критическая точка
. Если при этом критическая точка  разделяет промежутки выпуклости противоположных направлений, то
разделяет промежутки выпуклости противоположных направлений, то  .
. ,
,  .
. .
. .
.







 ;
; ;
; .
. .
. .
. .
.
 .
.
 .
. .
. .
.









 .
.




 y
y или
или  .
. .
. 2.
2. 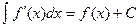 ;
;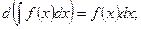 4.
4.  ;
; ; 6.
; 6.  .
.




















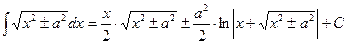
 .
.



 .
. .
.
 .
.


 ,где
,где  и получают
и получают 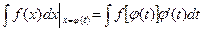
 , которое находится из соотношения
, которое находится из соотношения  .
.












 =
=  .
. . Разобьем отрезок на n частей точками
. Разобьем отрезок на n частей точками  , выберем на каждом элементарном отрезке
, выберем на каждом элементарном отрезке  произвольную точку xk и обозначим через
произвольную точку xk и обозначим через  длину каждого такого отрезка.
длину каждого такого отрезка.





