Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
И методические указания по выполнению дкр и дзСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для проведения промежуточной аттестации
ЕН.01 МАТЕМАТИКА ДЛЯ СТУДЕНТОВ ЗАОЧНОГО ОТДЕЛЕНИЯ Форма проведения оценочной процедуры Дифференцированные контрольные работы и дифференцированный зачет ( письменные)
Первоуральск
СОГЛАСОВАНО на заседании методической комиссии №___ «____»_____________2015 года __________руководитель МК Игнатьева Т.А.
ПРИНЯТО Протокол методического совета № _____ от «____»____________ 2015 г. __________председатель МС Л.А. Ленькова
СОГЛАСОВАНО _____________________________ _____________________________должность, ФИО от «____»_______________ 2015 г.
Разработчик: ФИО, должность, квалификационная категория _______________ Борисова Антонина Петровна преподаватель математики
______________ первой квалификационной категории
СОДЕРЖАНИЕ
Введение……………………………………………………………………….............4 Тематика контрольных работ и зачета..……………………………………………4 Методические указания по выполнению контрольных работ и зачета ….……...4 Краткие теоретические сведения и образцы решения задач…………...…………5 Задания контрольных работ………………………………………………………...29 Список рекомендуемой литературы………………………………………………..35 ВВЕДЕНИЕ Задания для контрольных работ и методические указания по их выполнению разработаны по учебной дисциплине «математика», входящей в математический и общий естественнонаучный цикл программы подготовки квалифицированных рабочих и служащих в соответствии с требованиями федерального государственного образовательного стандарта среднего профессионального образования, с рабочей программой дисциплины «математика» для студентов заочной формы обучения. ТЕМАТИКА КОНТРОЛЬНЫХ РАБОТ Раздел 1. Основы линейной алгебры. Раздел 2. Основы математического анализа. Раздел 3. Основы теории вероятностей. Раздел 4. Последовательности и ряды.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ Контрольная работа имеет 10 вариантов. Вариант контрольной работы выбирается по последней цифре шифра зачетной книжки. Работы, выполненные не по своему варианту, не засчитываются и возвращаются студенту без оценки. Студент должен ознакомиться с рецензией преподавателя, исправить все ошибки, допущенные в работе, а в случае неудовлетворительного выполнения работы исправить её и представить вторично или по указанию преподавателя выполнить другой вариант и представить его на рецензию.
При выполнении контрольной работы надо помнить следующие правила: · каждая работа выполняется в отдельной тетради в клетку в рукописном варианте; · контрольные работы должны быть написаны чернилами, аккуратно и разборчиво, для пометок преподавателя должны быть оставлены поля; · контрольная работа должна содержать: 1. титульный лист, с указанием ФИО студента, его группу и шифр по зачетной книжке; 2. основной раздел, где каждая контрольная работа начинается с новой страницы; 3. каждое задание работы должно содержать условие, решение и ответ. Замечания рецензента стирать и исправлять нельзя, все проверенные контрольные работы сохраняются и представляются на дифференцированном зачете. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ И ОБРАЗЦЫ РЕШЕНИЯ ЗАДАЧ Раздел 1. Элементы линейной алгебры. Тема 1.1 Матрицы и определители. Матрица – это прямоугольная таблица каких-либо элементов. В качестве элементов мы будем рассматривать числа, то есть числовые матрицы. ЭЛЕМЕНТ – это термин. Термин желательно запомнить, он будет часто встречаться, не случайно я использовал для его выделения жирный шрифт. Обозначение: матрицы обычно обозначают прописными латинскими буквами Пример: рассмотрим матрицу «два на три»:
Данная матрица состоит из шести элементов: Рассматриваемая матрица имеет две строки: СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали матрицу «два на три». Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например: Если в матрице один столбец Действия с матрицами: Умножение матрицы на число. Пример 1:
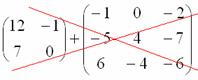
Для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку. Сумма (разность) матриц. Сумма матриц действие несложное. НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ. Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой! Пример 2: Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:
Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов. Пример 3:
Умножение матриц.
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 430; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.205.148 (0.007 с.) |

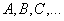





 – матрица «три на три».
– матрица «три на три». или одна строка
или одна строка  , то такие матрицы также называют векторами.
, то такие матрицы также называют векторами.
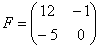 и
и