
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Какие матрицы можно умножать.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Чтобы матрицу Пример 4:
А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!
Следует отметить, что в ряде случаев можно умножать матрицы и так, и так. Как умножить матрицы? Начнем с самого простого: Пример 5:
Пример 6 (сложнее): Умножить матрицу Формула:
В результате получена так называемая нулевая матрица. Попробуйте самостоятельно выполнить умножение Обратите внимание, что Если в задании предложено умножить матрицу Переходим к матрицам третьего порядка: Умножить матрицу Формула очень похожа на предыдущие формулы:
А теперь попробуйте самостоятельно разобраться в умножении следующих матриц: Умножьте матрицу Вот готовое решение, но постарайтесь сначала в него не заглядывать!
Определитель первого порядка равен тому единственному элементу, из которого состоит соответствующая матрица. Определителем второго порядка называется число Определителем третьего порядка называется число
Основные свойства определителей: 1. Если строки определителя поменять местами с соответственными столбцами, то значение определителя не изменится. 2. Если переставить две строки (столбца) определителя местами, то значение определителя изменится на противоположное. 3. Если элементы строки (столбца) определителя содержат общий множитель, то его можно вынести за знак определителя. 4. Если две строки (столбца) определителя содержат соответственно пропорциональные элементы, то значение определителя равно нулю. 5. Если к элементам какой-либо строки (столбца) определителя прибавить соответственные элементы другой строки (столбца), умноженные на одно и то же число, то значение определителя не изменится. Пример 7: Вычислить определитель: Упростив определитель согласно перечисленным свойствам, найдем его значение: 1) вынесем множитель 3 из второй строки за знак определителя; 2) сложим соответственные элементы первой и второй строки; 3) сложим соответственно элементы второго и третьего столбца; 4) вынесем множитель 2 из второго столбца за знак определителя; 5) вынесем множитель 3 из первой строки за знак определителя; 6) вычислим определитель по правилу.
Тема 1.2. Системы линейных уравнений. Решение систем линейных уравнений методом определителей (метод Крамера) Рассмотрим систему трех линейных уравнений с тремя неизвестными: x 1, x 2, x 3:
(коэффициенты aij и свободные члены bi считаются заданными). Решение: составим определители
где D называют определителем системы, а определители D xi получены из основного определителя D заменой свободными членами bi элементов соответствующего столбца.
Особые случаи: 1) если D¹ 0, то система имеет единственное решение; 2) если D = 0, D xi ¹ 0, то система несовместна; 3) если D = D xi = 0, то система либо имеет бесконечное множество решений, либо она решений не имеет. Пример 1: Решить систему линейных уравнений: Решение: составим определители D, D x, D y, D z и найдем их значения.
Найдем решение системы: Ответ: (3; 2; –1). Раздел 2. Основные понятия и методы математического анализа. Тема 2.1. Теория пределов. Определение: Число А называется пределом функции y=f(х) при х, стремящемсяк а, если для любой последовательности чисел х1, х2, х3, …,.хn,… сходящейся к числу а, следует, что последовательность значений функции f(х1), f(х2),…, f(хn)… сходится к числу А. Предел функции в точке а обозначается Основные теоремы о пределах Приведем основные теоремы, на которых основано вычисление пределов: 1. 2. 3. 4. 5. 6.
Техника вычисления пределов При вычислении предела элементарной функции f(x) приходится сталкиваться с двумя существенно различными типами примеров. · Функция f(x) определена в предельной точке x = a. Тогда · Функция f(x) в предельной точке x = a не определена или же вычисляется предел функции при x→∞. Тогда вычисление предела требует в каждом случае индивидуального подхода. Необходимо помнить, что Более сложными случаями нахождения предела являются такие, когда функция f(x) в точке x = a или при x→∞ представляет собой неопределенность (типа При вычислении пределов при а) чтобы раскрыть неопределенность типа б) чтобы раскрыть неопределенность типа в) чтобы раскрыть неопределенность типа г) чтобы раскрыть неопределенность типа д) чтобы раскрыть неопределенность типа Вычислить пределы функций: Пример 1:
Пример 2: Пример 3: = Пример 4:
Пример5:
Тема 2.2. Дифференциальное исчисление. Понятие производной Определение: Производной функции
Если этот предел конечный, то функция y=f(x) называется дифференцируемой в точке x. Если же этотпредел есть ∞, то говорят, что функция y=f(x) имеет в точке x бесконечную производную.
Механический смысл производной: скорость есть первая производная пути по времени, т.е. Геометрический смысл производной: тангенс угла наклона касательной к графику функции Уравнение касательнойк графику функции
Уравнение нормали к графику функции
Таблица производных
Процесс нахождения производных называется дифференцированием функции.
Найти производные функций: Пример 1: Решение:
Пример2: Решение: Пример 3: Решение:
Дифференциал функции Определение: Дифференциалом функции y=y(x) называется произведение ее производной на дифференциал независимой переменной: Пример 1: Найти дифференциал функции Решение: Так как Дифференцирование сложной функции
Пусть y= y(u), где u= u(x) – дифференцируемые функции. Тогда сложная функция y=y[u(x)] есть также дифференцируемая функция, причем
Это правило распространяется на цепочку из любого конечного числа дифференцируемых функций: производная сложной функции равна произведению производных функций, ее составляющих. Производные сложных функций находятся при помощи таблицы:
Пример 1: Найти производную функции Решение: Пример 2: Найти производную функции Решение:
=
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 3445; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.34.39 (0.01 с.) |

 можно было умножить на матрицу
можно было умножить на матрицу  необходимо, чтобы число столбцов матрицы
необходимо, чтобы число столбцов матрицы  на матрицу
на матрицу  ?
?
 , значит, умножать данные матрицы можно.
, значит, умножать данные матрицы можно.
 , следовательно, выполнить умножение невозможно, и вообще, такая
, следовательно, выполнить умножение невозможно, и вообще, такая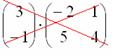
 и
и  возможно как умножение
возможно как умножение  , так и умножение
, так и умножение 
 на матрицу
на матрицу  – попытайтесь сразу уловить закономерность.
– попытайтесь сразу уловить закономерность.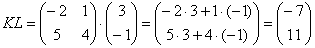


 ).
). ! Таким образом, переставлять матрицы в произведении нельзя!
! Таким образом, переставлять матрицы в произведении нельзя! на матрицу
на матрицу  , то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.
, то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот. на матрицу
на матрицу 



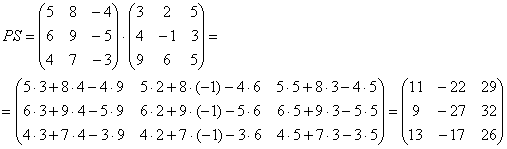
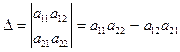 .
.



 :
: ,
,  ,
,  ,
,  ,
,

 (D¹ 0, следовательно, система имеет единственное решение).
(D¹ 0, следовательно, система имеет единственное решение). .
. .
. .
.

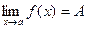 .
.


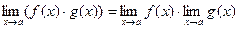


 .
. ,
,  ,
, 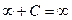 ,
,  ,
,  ,
,  .
. 
 ,
,  ,
, 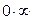 ,
,  ,
,  ,
,  ,
,  ).
). основные теоремы о пределах сохраняют силу и, кроме того, используются правила:
основные теоремы о пределах сохраняют силу и, кроме того, используются правила: , необходимо числитель и знаменатель дроби разделить на наибольшую степень переменной;
, необходимо числитель и знаменатель дроби разделить на наибольшую степень переменной; , необходимо числитель и знаменатель дроби разделить на наименьшую степень переменной;
, необходимо числитель и знаменатель дроби разделить на наименьшую степень переменной;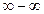 , необходимо числитель и знаменатель дроби одновременно умножить на сопряженное выражение и тем самым свести к неопределенности вида
, необходимо числитель и знаменатель дроби одновременно умножить на сопряженное выражение и тем самым свести к неопределенности вида 







 по аргументу x называется предел отношения ее приращения
по аргументу x называется предел отношения ее приращения  к приращению
к приращению  аргумента x, когда приращение аргумента стремится к нулю:
аргумента x, когда приращение аргумента стремится к нулю: .
. .
.
 :
:


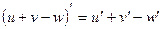





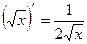

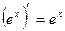







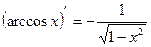



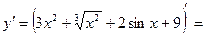


 +
+






 .
.

 , то
, то  .
. , или
, или 


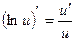


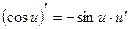









 =
= 





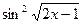 +
+




