
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Действия с матрицами
Данная матрица состоит из шести элементов:
Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет:
Это просто таблица (набор) чисел! Также договоримся не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя! Рассматриваемая матрица имеет две строки:
три столбца:
СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три». Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например:
– матрица «три на три». Если в матрице один столбец
или одна строка
то такие матрицы также называют векторами. Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу). Вернемся к нашей матрице
Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит. Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак:
Действие второе. Умножение матрицы на число. Пример:
Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку. Еще один полезный пример:
– умножение матрицы на дробь Сначала рассмотрим то, чего делать НЕ НАДО:
И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:
Мы помним, что десятичных дробей с запятой в высшей математике стараются всячески избегать. Единственное, что желательно сделать в этом примере – это внести минус в матрицу:
А вот если бы ВСЕ элементы матрицы делились на 7 без остатка, то тогда можно (и нужно!) было бы поделить. Пример:
В этом случае можно и НУЖНО умножить все элементы матрицы на 1/2, так как все числа матрицы делятся на 2 без остатка. Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление – это частный случай умножения.
Действие пятое. Умножение матриц. Как умножить матрицы? Пример: Умножить матрицы
Я буду сразу приводить формулу для каждого случая:
– попытайтесь сразу уловить закономерность.
Пример сложнее: Умножить матрицы
Формула:
В результате получена так называемая нулевая матрица. Если в задании предложено умножить матрицу M на матрицу N, то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот. Переходим к матрицам третьего порядка: Умножить матрицуы
Формула очень похожа на предыдущие формулы:
А теперь попробуйте самостоятельно разобраться в умножении следующих матриц: Умножьте матрицы
Ответ.
Как проверить решение? Необходимо выполнить матричное умножение Проверка:
Получена так называемая единичная матрица (с единицами по главной диагонали и нулями в остальных местах). Таким образом, обратная матрица найдена правильно. Пример: Найти обратную матрицу для матрицы
Обратную матрицу найдем по формуле:
где Как вычислить определитель? Определитель можно вычислить только для квадратной матрицы. Обозначения: Если дана матрица
то ее определитель обозначают |A|. Также очень часто определитель обозначают латинской буквой D или греческой Δ. 1) Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. 2) Теперь осталось разобраться в том, КАК найти это число. Как Вы догадываетесь, для этого нужно применить определенные правила, формулы и алгоритмы, о чём сейчас и пойдет речь. Начнем с определителя «два» на «два»:
Сразу рассмотрим пример:
Определитель матрицы «три на три» можно раскрыть 8 способами, 2 из них простые и 6 - нормальные. Начнем с двух простых способов Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:
Пример:
Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:
Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс». Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус: Пример:
Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше. Правило Крамера. А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если D=0, то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет/ Если D≠0, то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
И, наконец, ответ рассчитывается по формулам:
Пример Решить систему по формулам Крамера.
Решение: Решим систему по формулам Крамера.
значит, система имеет единственное решение.
Ответ: Собственно, здесь опять комментировать особо нечего. Но есть пара замечаний. Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так: 1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие. Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу). 2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная
– на месте отсутствующих переменных ставятся нули. Пример Решить систему матричным методом
Решение: Запишем систему в матричной форме: AX=b, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице A нужно было бы поставить нули.
Согласно формуле нам нужно найти обратную матрицу Обратную матрицу найдем по формуле:
где
Сначала разбираемся с определителем:
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент В ходе решения расчет миноров лучше расписать подробно.
Порядок расчета миноров совершенно не важен, здесь я их вычислил слева направо по строкам. Можно было рассчитать миноры по столбцам (это даже удобнее). Таким образом:
– матрица миноров соответствующих элементов матрицы A.
– матрица алгебраических дополнений.
– транспонированная матрица алгебраических дополнений. Теперь записываем обратную матрицу:
Ни в коем случае не вносим
Обратите внимание, что деление на 60 выполняется в последнюю очередь. Ответ:
Действия с матрицами
Данная матрица состоит из шести элементов:
Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет:
Это просто таблица (набор) чисел! Также договоримся не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя! Рассматриваемая матрица имеет две строки:
три столбца:
СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три». Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например:
– матрица «три на три». Если в матрице один столбец
или одна строка
то такие матрицы также называют векторами. Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу). Вернемся к нашей матрице
Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит.
Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак:
|
||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1910; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.185.143 (0.013 с.) |








 ,
,












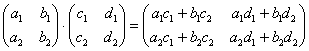
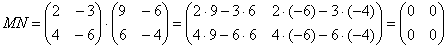




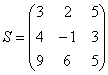


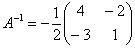
 либо
либо 


 ,
, – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы  .
. ,
,









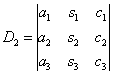













 ..
..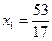 .
.
 , во втором – переменная
, во втором – переменная  . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
. В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:

 .
. и выполнить матричное умножение
и выполнить матричное умножение  . Алгоритм нахождения обратной матрицы подробно разобран в разделе «Как найти обратную матрицу?»
. Алгоритм нахождения обратной матрицы подробно разобран в разделе «Как найти обратную матрицу?» – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы A.
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы A.


 находится в первой строке, третьем столбце, а, например, элемент
находится в первой строке, третьем столбце, а, например, элемент 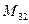 находится в 3 строке, 2 столбце.
находится в 3 строке, 2 столбце.












 в матрицу, это серьезно затруднит дальнейшие вычисления. Деление нужно было бы выполнить, если бы все числа матрицы делились на 60 без остатка. А вот внести минус в матрицу в данном случае очень даже нужно, это, наоборот – упростит дальнейшие вычисления.
в матрицу, это серьезно затруднит дальнейшие вычисления. Деление нужно было бы выполнить, если бы все числа матрицы делились на 60 без остатка. А вот внести минус в матрицу в данном случае очень даже нужно, это, наоборот – упростит дальнейшие вычисления.



