
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Находим определитель матрицы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
а значит, всё нормально – обратная матрица существует. 2) Находим матрицу миноров M Матрица миноров имеет размерность «три на три»
и нам нужно найти девять чисел. Я подробно рассмотрю парочку миноров: Рассмотрим следующий элемент матрицы:
Оставшиеся четыре числа записываем в определитель «два на два»
Этот определитель «два на два» и является минором данного элемента. Его нужно вычислить:
Всё, минор найден, записываем его в нашу матрицу миноров:
Как Вы, наверное, догадались, необходимо вычислить девять определителей «два на два». Ну и для закрепления – нахождение еще одного минора в картинках:
Остальные миноры попробуйте вычислить самостоятельно. Окончательный результат:
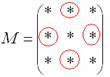
– матрица миноров соответствующих элементов матрицы B. 3) Находим матрицу алгебраических дополнений В матрице миноров необходимо СМЕНИТЬ ЗНАКИ строго у следующих элементов:
В данном случае:
– матрица алгебраических дополнений соответствующих элементов матрицы B. 4) Находим транспонированную матрицу алгебраических дополнений
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы 5) Ответ:
Проверка:
Таким образом, обратная матрица найдена правильно. Как вычислить определитель? Определитель можно вычислить только для квадратной матрицы. Обозначения: Если дана матрица
то ее определитель обозначают |A|. Также очень часто определитель обозначают латинской буквой D или греческой Δ. 1) Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. 2) Теперь осталось разобраться в том, КАК найти это число. Как Вы догадываетесь, для этого нужно применить определенные правила, формулы и алгоритмы, о чём сейчас и пойдет речь. Начнем с определителя «два» на «два»:
Сразу рассмотрим пример:
Определитель матрицы «три на три» можно раскрыть 8 способами, 2 из них простые и 6 - нормальные. Начнем с двух простых способов Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:
Пример:
Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок». Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:
Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс». Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус: Пример:
Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.
|
||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 640; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 ,
, ,
,








 .
.
 .
.
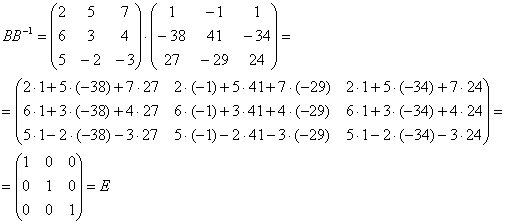
 ,
,









