
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условные законы распределенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Как было показано выше, зная закон распределения системы (заданный в виде функции распределения или плотности распределения), можно найти законы распределения составляющих системы. Обратную задачу в общем случае решить нельзя, т.е. зная законы распределения составляющих, невозможно найти закон распределения системы в целом. Причина этого кроется в следующем. Для того чтобы исчерпывающим образом охарактеризовать систему, недостаточно знать распределение каждой из величин, входящих в систему; нужно еще знать зависимость между величинами, входящими в систему. Эта зависимость может быть охарактеризована с помощью условных законов распределения. Рассмотрим систему дискретных случайных величин Х и Y. Используя теорему умножения вероятностей зависимых событий, выразим вероятность того, что составляющая Х примет значение хi, а Y – значение yj: Р(хi, yj) = Р(хi)Р(yj|xi). Аналогично Р(yj, xi) = Р(yj)Р(xi|yj). Отсюда можно выразить Р(yj|xi) и Р(xi|yj): Р(yj|xi)= Р(хi, yj)/ Р(хi), Р(xi|yj)= Р(yj, xi)/ Р(yj).
Задача. Найти условный закон распределения составляющей Х при условии, что составляющая Y приняла значение у = 2.
Решение. Безусловный закон распределения Х имеет вид:
Найдем Р (У =2) = 0,05 + 0,15 = 0,2. После того, как составляющая Y приняла значение 2, закон распределения Х представляется так:
Как видно, результаты заметно отличаются.
Теперь рассмотрим непрерывную систему случайных величин (Х, Y). Аналогично случаю дискретного распределения системы можно показать, что
где Т.о., плотность распределения системы двух величин равна плотности распределения одной из величин, входящих в систему, умноженной на условную плотность распределения другой величины, вычисленную при условии, что первая величина приняла заданное значение. Указанные выше формулы часто называют теоремой умножения законов распределения. Э та теорема в схеме случайных величин аналогична теореме умножения вероятностей в схеме событий. Разрешив формулы относительно
а применив формулы
Задача. Случайная величина (Х, Y) равномерно распределена внутри эллипса Решение. В данном случае
или
где D – данный эллипс. Известно, что Безусловные плотности распределения составляющих Х и Y найдем, взяв интегралы по переменным у и х соответственно:
Теперь выразим условные плотности распределения составляющих Х и Y:
Контрольные вопросы
1. Что называется функцией распределения системы случайных величин Х и Y? 2. Сформулируйте свойства функции распределения системы случайных величин Х и Y. 3. Как определить функции распределения составляющих системы с.в. (Х; Y), зная функцию совместного распределения системы (Х; Y)? 4. Каким образом выглядят формулы попадания случайной величины (Х; Y): а) в полуполосу, параллельную оси О х; б) в полуполосу, параллельную оси О у; в) в прямоугольник? 5. Что называется плотностью совместного распределения системы (Х; Y)? 6. Как определить вероятность попадания непрерывной с.в. (Х; Y) в область D? 7. Как определить плотности распределения составляющих системы с.в. (Х; Y), зная плотность совместного распределения системы (Х; Y)? 8. Что называется условным законом распределения системы (Х; Y)? 9. Каким образом можно найти условный закон распределения составляющей Х при условии, что составляющая Y приняла значение, равное у, если: а) Х; Y – дискретные с.в.; б) Х; Y – непрерывные с.в.?
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 722; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.241.235 (0.006 с.) |

 ,
, ,
, ,
,  - плотности распределения составляющих Х и Y соответственно, а
- плотности распределения составляющих Х и Y соответственно, а  и
и  - условные плотности распределения Y и Х, вычисленные при условии, что другая величина приняла заданное значение.
- условные плотности распределения Y и Х, вычисленные при условии, что другая величина приняла заданное значение. ,
, ,
,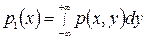 и
и  , получим
, получим ,
,  .
. . Найти безусловные и условные плотности распределения составляющих.
. Найти безусловные и условные плотности распределения составляющих. (с = const) внутри эллипса, вне эллипса
(с = const) внутри эллипса, вне эллипса  . Константу с найдем, воспользовавшись характеристическим свойством двумерной плотности вероятности
. Константу с найдем, воспользовавшись характеристическим свойством двумерной плотности вероятности  , из уравнения
, из уравнения

 , где
, где  – площадь области D. В данном случае
– площадь области D. В данном случае  . Подставляя это значение в последнее уравнение, выражаем с:
. Подставляя это значение в последнее уравнение, выражаем с:  . Таким образом, плотность совместного распределения Х и Y имеет вид:
. Таким образом, плотность совместного распределения Х и Y имеет вид: 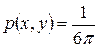 .
.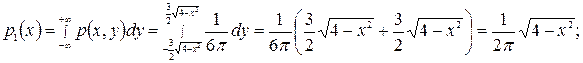

 ,
, .
.


