
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение комбинаторных формул для вычисления вероятностей в классической схемеСодержание книги
Поиск на нашем сайте
Элементы комбинаторики При подсчете числа элементарных исходов при классическом определении вероятности часто оказываются полезными различные комбинаторные формулы. Приведем наиболее распространенные из них. Пусть имеется конечное множество Упорядоченные наборы, т. е. наборы, отличающиеся не только составом элементов, но и их порядком следования, называют размещениями, а неупорядоченные – сочетаниями. Например, из множества Размещения. Число всех размещений из
Напомним, что по определению Для
Перестановки. Учитывая, что перестановками называются размещения из
Для
Сочетания. Два сочетания из
Для чисел
В теории вероятностей часто математические модели, имеющие приложения в самых различных областях, формулируются в терминах схемы урн, т. е. идеализированного опыта по выбору наудачу
А. Схема выбора, приводящая к сочетаниям без повторений элементов. Если опыт состоит в случайном выборе
Пример. Из урны, содержащей 10 белых и 5 черных шаров, наудачу без возвращения извлекается три шара. Какова вероятность извлечь три белых шара? ◄ Слово «наудачу» в условии задачи означает, что шары были хорошо перемешаны, что все они одного диаметра, одинаково гладкие и отличаются только цветом; выбирающий шаров не видит. В таком случае разумно предположить равновероятность элементарных исходов и воспользоваться классическим определением вероятности. За элементарные исходы естественно принять любые подмножества по три элемента, выбранные из множества из 15 шаров. Так как порядок извлеченных шаров нас не интересует, то под исходом следует понимать любое сочетание трех элементов из 15. Число таких сочетаний
Б. Схема выбора, приводящая к размещениям без повторений элементов. Если опыт состоит в выборе
В частном случае
Пример. На пяти карточках написаны цифры от 1 до 5. Опыт состоит в случайном выборе трех карточек и раскладывании их в порядке поступления слева направо. Найти вероятность события ◄ В качестве равновероятных элементарных исходов данного опыта выступают упорядоченные наборы трех карточек из пяти (размещения из пяти элементов по три). Их общее число
В. Схема выбора, приводящая к сочетаниям с повторениями элементов. Если опыт состоит в выборе с возвращением
Пример. В кондитерской имеется 7 видов пирожных. Очередной покупатель приобрел 4 пирожных. Считая, что любой набор пирожных равновероятен, найти вероятность того, что покупатель приобрел по два пирожных различных видов. ◄ Число всех равновероятных исходов данного опыта равно, очевидно, числу сочетаний с повторениями из 7 элементов по 4, т. е. Число исходов, благоприятствующих событию
Г. Схема выбора, приводящая к размещениям с повторениями элементов. Если выбор
Пример. Бросается пять игральных костей. Найти вероятность того, что на них выпадут различные цифры. ◄ Бросание пяти игральных костей смоделируем схемой урн: из урны, в которую помещены 6 карточек с нанесенными на них цифрами от 1 до 6, выбираем наудачу с возвращением пять раз карточки с упорядочиванием их в последовательную цепочку. Появление той или иной цифры на карточке в цепочке будет соответствовать выпадению этого числа очков на соответствующей кости. Очевидно, что элементарные исходы в данном опыте представляют собой размещения с повторениями при
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 376; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.26.8 (0.006 с.) |

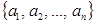 , состоящее из
, состоящее из  различных элементов. Из этого множества можно образовать различные наборы (подмножества), состоящие из
различных элементов. Из этого множества можно образовать различные наборы (подмножества), состоящие из 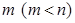 элементов.
элементов.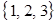 , выбирая по два элемента (
, выбирая по два элемента (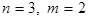 ) можно образовать шесть размещений:
) можно образовать шесть размещений: 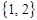 ,
, 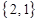 ,
, 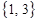 ,
, 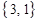 ,
, 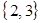 ,
, 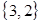 ; и три сочетания
; и три сочетания 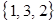 ,
, 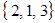 ,
, 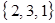 ,
, 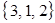 ,
, 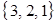 .
. обозначают символом
обозначают символом 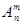 . Различными считаются размещения, в которых имеются различные элементы, или, если все элементы одни и те же, различен порядок их расположения. Число
. Различными считаются размещения, в которых имеются различные элементы, или, если все элементы одни и те же, различен порядок их расположения. Число 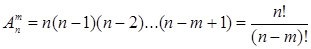 . (3)
. (3)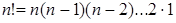 , причем
, причем 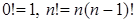 .
.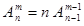 .
.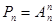 согласно (3) будем иметь:
согласно (3) будем иметь: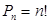 .
.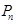 справедлива следующая рекуррентная формула:
справедлива следующая рекуррентная формула: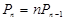 .
.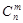 . Число
. Число 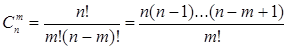 .
.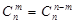 (свойство симметрии),
(свойство симметрии),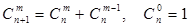 (рекуррентное соотношение),
(рекуррентное соотношение),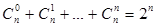 (следствие биномиальной формулы Ньютона).
(следствие биномиальной формулы Ньютона).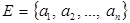 . При этом строго оговаривается, каким способом производится случайный выбор и что понимается под различными выборками. Существуют две принципиально отличные схемы выбора: без возвращения элементов и с возвращением. В первой схеме отбираются либо сразу все
. При этом строго оговаривается, каким способом производится случайный выбор и что понимается под различными выборками. Существуют две принципиально отличные схемы выбора: без возвращения элементов и с возвращением. В первой схеме отбираются либо сразу все  .
.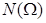 =
= 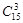 . Событию
. Событию  ={все три извлеченных шара окажутся белыми} благоприятствует
={все три извлеченных шара окажутся белыми} благоприятствует 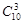 исходов (вынимаются какие-то три белых шара из 10 белых):
исходов (вынимаются какие-то три белых шара из 10 белых): 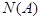 =
= 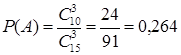 . ►
. ►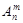 .
.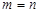 опыт фактически состоит в произвольном упорядочивании множества
опыт фактически состоит в произвольном упорядочивании множества 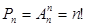 .
.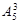 . Наборы, благоприятствующие рассматриваемому событию, представляют также упорядоченные наборы трех карточек, но из четырех карточек (цифру 3 исключаем из исходного множества), т. е.
. Наборы, благоприятствующие рассматриваемому событию, представляют также упорядоченные наборы трех карточек, но из четырех карточек (цифру 3 исключаем из исходного множества), т. е. 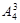 . По формуле классической вероятности получаем:
. По формуле классической вероятности получаем: 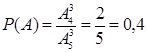 . ►
. ►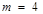 наборы
наборы 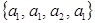 и
и 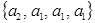 неразличимы для данного опыта, набор
неразличимы для данного опыта, набор 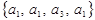 отличен от любого из предыдущих. Получающиеся в результате данного опыта комбинации называются сочетаниями с повторениями, а их общее число определяется формулой
отличен от любого из предыдущих. Получающиеся в результате данного опыта комбинации называются сочетаниями с повторениями, а их общее число определяется формулой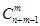 .
.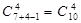 .
.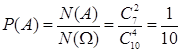 . ►
. ►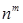 .
.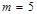 и
и 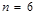 , т. е.
, т. е. 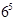 . Событию
. Событию 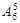 . Таким образом,
. Таким образом, 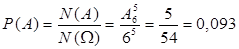 . ►
. ►


