
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайные величины в общей схемеСодержание книги
Поиск на нашем сайте
В случае произвольного вероятностного пространства случайной величиной
Функция распределения обладает следующими свойствами:
a) 0 ≤ b) FX (– c) d) Вероятность попадания случайной величины X на произвольный интервал действительной оси (
Различают случайные величины дискретного типа и случайные величины непрерывного типа. Определение дискретных случайных величин и их законов распределения дано выше. Зная закон распределения таких величин, можно вычислить функцию распределения, представляющую собой, в силу определения (3), функцию накопленных вероятностей:
где суммирование распространяется на все значения индекса Случайная величина Х называется случайной величиной непрерывного типа, если существует такая неотрицательная функция
Плотность распределения вероятностей обладает следующими свойствами: a) b) c) Функция распределения непрерывной случайной величины
Это значит, что вероятность «попасть в точку» для непрерывной случайной величины, равна нулю. Если Х - непрерывная случайная величина, то вероятность ее попадания на интервал (
Пример. Функция
◄ Постоянную Функцию распределения найдем исходя из определяющей ее формулы (6): По формуле (7) находим искомую вероятность
= –
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 196; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.166.45 (0.007 с.) |

 называется такая функция X = X (
называется такая функция X = X ( ) от элементарных исходов
) от элементарных исходов  , для которой при любом численном значении
, для которой при любом численном значении 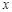 неравенство { X ≤
неравенство { X ≤  { X ≤
{ X ≤  случайной величины X определяется формулой
случайной величины X определяется формулой < x <
< x < 
 =
=  .
. ,
,  ] определяется формулой
] определяется формулой =
=  –
–  . (4)
. (4) (5)
(5) 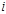 , для которых
, для которых  <
<  .
. , называемая плотностью распределения вероятностей, что при всех
, называемая плотностью распределения вероятностей, что при всех  R
R =
=  . (6)
. (6) =l (условие нормировки);
=l (условие нормировки); =
=  = 0 при всех x
= 0 при всех x  . (7)
. (7) является плотностью распределения некоторой непрерывной случайной величины. Найти: значение нормирующей постоянной
является плотностью распределения некоторой непрерывной случайной величины. Найти: значение нормирующей постоянной  , функцию распределения, вероятность
, функцию распределения, вероятность =
=  =
=  =
= 

 . Итак,
. Итак,  .
. =
=  =
=  .
. =
=  =
=  =
=  =
= . Этот результат можно получить и с помощью функции распределения по формуле(4):
. Этот результат можно получить и с помощью функции распределения по формуле(4):  =
=  –
–  =
=  –
– =
=  . ►
. ►


