
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Какие множества называются эквивалентными. Каким условиям удовлетворяет отношение эквивалентности.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если между элементами множеств А и В установлено взаимно однозначное соответствие, то такие множества называются эквивалентными, что обозначается как А ~ В. Отношение эквивалентности удовлетворяет следующим условиям: рефлексивность: А ~ А; симметричность: если А ~ В, то В ~ А; транзитивность: если А ~ В и В ~ С, то А ~ С Равные множества эквивалентны. Из эквивалентности множеств равенство в общем случае не следует. 4. Множества А и В – конечны, А ~ В. nA – мощность множества А, nВ – мощность множества В. Какое из приведенных соотношений правильно: а) nA > nВ; б) nA < nВ; в) nA = nВ + 1; г) nA = nВ; д) nВ = nA + 1? 5. Операции объединения и пересечения являются коммутативными А È В = В È А и А Ç В = В Ç А Продолжите равенство: А Ç (В È С) = (А Ç В)Ç С) 6. Изобразите на диаграмме Эйлера–Венна множество (А + С)(В + С) и убедитесь в том, что оно равно АВ + С. 7. В чем состоит операция декартового произведения множеств? Что называют степенью множества? Пусть R – множество вещественных чисел. Какие множества будут получены в результате операций R ´ R и R ´ R ´ R? Декартовым произведением множеств А и В называется множество D, элементами которого называются всевозможные упорядоченные пары элементов множеств А и В, обозначаемые как < a, b >, т. е. D = A ´ B = { d; d = < a, b >, a Î A, B Î B }. Степенью множества называют п-кратное декартово произведение множества на самого себя. R ´ R = R2 является множеством всех точек на плоскости, R ´ R ´ R – множество всех точек пространства, а степень порядка n множества R определяет множество п-мерных векторов Rn. 8. Что такое мощность конечных множеств? Для множеств A = {–2, 0, 1, 4, 9} и B = {–2, 4, 3, 1} найдите А È В, А Ç В, А \ В, В \ А и А D В. Определите мощность получаемых в результате данных операций множеств. Число элементов эквивалентных между собой конечных множеств определяет мощность этих множеств. АÈВ ={-2,0,1,3,4,9} М=6 АÇВ={-2,1,4} М=3 А \ В={0,9} М=2В \ А={3} М=1 А D В={0,3,9} М=3
9. Множества С и D имеют мощности, равные 10. Установите, какие из приведенных ниже выражений правильны: а) (А È В) \ С = А È (В \ С) - нет; б) АВС = АВ (С È В) - нет; 11. Установите, какие из приведенных ниже выражений правильны: а) А È В = (А \ АВ) È В - да; б) А È В = (А D В)D(А Ç В) - да; в) (АВ È ВС È СА) Ì (А È В È С) - да. 12. Симметрическая разность множеств А и В - объединение двух разностей А \ В и В \ А. Симметрическая разность обозначается символом D: А D В = (А \ В) È (В \ А) Продолжите равенство: А Ç (В \ С) = (А Ç В) \ С Что называют единичным (нейтральным) элементом по отношению к бинарной операции? Что называют обратным элементом по отношению к бинарной операции? Что представляют собой нейтральный и обратный элементы по отношению к операциям сложения и умножения на множестве вещественных чисел? Единичный (нейтральный) элемент по отношению к введенной бинарной операции - элемент е Î А, такой, что для любого элемента а, принадлежащего множеству А, выполняется условие е * а = а * е = а. Обратный элемент по отношению к бинарной операции – элемент, который в сочетании с заданным элементом в рамках некоторой бинарной операции дает нейтральный элемент. а-1 * а = е На множестве вещественных чисел по отношению к операции сложения: 0 – нейтральный, -х – обратный; умножение: 1 – нейтральный, 1\х – обратный. х – элемент множества. 14. Дайте определения следующих алгебраических структур: полугруппа, моноид, группа, абелева группа. Какую алгебраическую структуру образует множество целых чисел Z по отношению к операции сложения? Ответ аргументируйте. Полугруппа – если имеем дело с бинарной ассоциативной операцией – результат операции попадает в то же множество и (а х b) х с = а х (b x c), где х – операция. Моноид – полугруппа + наличие нейтрального элемента
Группа – моноид + каждый элемент (кроме нейтрального и нулевого) обратим Абелева группа – группа + операция коммутативна (а+б=б+а) Множество целых чисел по операции сложение образует абелеву группу. Имеем дело с бинарной ассоциативной операцией; нейтральный элемент: 0; обратный элемент: -х; х+а=а+х. х и а – элементы. 15. Дайте определения следующих алгебраических структур: полугруппа, моноид, группа, абелева группа. Какую алгебраическую структуру образует множество вещественных чисел R по отношению к операции умножения? Ответ аргументируйте. Полугруппа – если имеем дело с бинарной ассоциативной операцией – результат операции попадает в то же множество и (а х b) х с = а х (b x c), где х – операция. Моноид – полугруппа + наличие нейтрального элемента Группа – моноид + каждый элемент (кроме нейтрального и нулевого) обратим Абелева группа – группа + операция коммутативна (а+б=б+а) Множество вещественных чисел по операции умножение образует абелеву группу. Имеем дело с бинарной ассоциативной операцией; нейтральный элемент 1; обратный элемент 1\х; х+а=а+х. х и а – элементы
16. Дайте определения следующих алгебраических структур: полугруппа, моноид, группа, абелева группа. Какую алгебраическую структуру образует множество натуральных чисел N по отношению к операции сложения? Ответ аргументируйте. Полугруппа – если имеем дело с бинарной ассоциативной операцией – результат операции попадает в то же множество и (а х b) х с = а х (b x c), где х – операция. Моноид – полугруппа + наличие нейтрального элемента Группа – моноид + каждый элемент (кроме нейтрального и нулевого) обратим Абелева группа – группа + операция коммутативна (а+б=б+а) Множество натуральных чисел по операции сложение образует полугруппу. Имеем дело с бинарной ассоциативной операцией, а нейтрального элемента уже нет. 17. Какая алгебраическая структура называется кольцом? Приведите пример кольца. Если множество по сложению абелева группа, а по умножению – моноид, то это кольцо. (Целые числа)
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 572; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.50.163 (0.011 с.) |

 Определите и проиллюстрируйте с помощью диаграмм Эйлера – Венна операции объединения и пересечения множеств. Являются ли эти операции коммутативными и ассоциативными? Запишите соответствующие соотношения.
Определите и проиллюстрируйте с помощью диаграмм Эйлера – Венна операции объединения и пересечения множеств. Являются ли эти операции коммутативными и ассоциативными? Запишите соответствующие соотношения.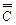 и
и 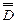 соответственно. Известно, что С и D не являются эквивалентными. Также известно, что в множестве C есть подмножество C*, эквивалентное множеству D. Какое из следующих нижеприведенных выражений правильно: а)
соответственно. Известно, что С и D не являются эквивалентными. Также известно, что в множестве C есть подмножество C*, эквивалентное множеству D. Какое из следующих нижеприведенных выражений правильно: а)  Сформулируйте и проиллюстрируйте с помощью диаграмм Эйлера – Венна определения разности множеств А и В, симметрической разности множеств А и В.
Сформулируйте и проиллюстрируйте с помощью диаграмм Эйлера – Венна определения разности множеств А и В, симметрической разности множеств А и В.


