
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дайте определение линейного пространства. Перечислите аксиомы лп.Содержание книги
Поиск на нашем сайте
Непустое множество L элементов 1. Для любых · · в L существует нулевой вектор · для " · " 2. Для " a Î F и · a(b · е · для " a, b Î F выполняется равенство (a + b) · " 26. Приведите примеры линейных пространств (не менее двух). 1. Совокупность действительных чисел с обычными арифметическими операциями сложения и умножения образует ЛП R 1. 2. Совокупность векторов 3. Непрерывные на отрезке [ a, b ] вещественные или комплексные функции с обычными правилами сложения функций и умножения на скаляр образуют ЛП С [ a, b ]. 4. Аналогично определяется ЛП, элементами которого являются функции с интегрируемым квадратом L 2[ a, b ] или L 2. Дайте определение линейной комбинации векторов из L. Вектор Дайте определение линейной независимости системы векторов из L. Бесконечная система векторов
Дайте определение базиса конечномерного ЛП. Какие важнейшие свойства базиса должны выполняться в ЛП? Если в L существует п линейно независимых векторов Свойства: 1. Любой вектор 2. Линейной оболочкой базисной системы векторов является само ЛП L 30. Приведите не менее трех примеров базисных систем для различных ЛП (с формулами или рисунками). В Rn или Сn базисной системой является совокупность п векторов вида В C [ a, b ] (множество функций, непрерывных на промежутке) базисную систему образует совокупность степенных функций { tn }, n = 0, 1, 2, … αn tn+ αn-1 tn-1+…+ α2t2+ αt+ αo В L2(множество функций с интегрируемым квадратом): {1+coskt,sinkt} Дайте определение скалярного произведения для ЛП. Перечислите свойства скалярного произведения. Скалярное произведение для ЛП, заданных над полями R или С, определяется аксиоматически как правило отображения любой упорядоченной пары < Приведите и докажите неравенство Коши-Буняковского для произвольных линейных пространств. Неравенство:
|
|||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 337; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.81.158 (0.007 с.) |

 ,
, 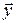 ,
,  , … (L может быть конечным, счетным или несчетным, его элементы могут быть векторами, матрицами или функциями) называется линейным (векторным) пространством, если выполняются следующие условия, называемые аксиомами ЛП:
, … (L может быть конечным, счетным или несчетным, его элементы могут быть векторами, матрицами или функциями) называется линейным (векторным) пространством, если выполняются следующие условия, называемые аксиомами ЛП: такой, что для "
такой, что для "  называется линейной комбинацией векторов
называется линейной комбинацией векторов 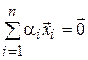 .
.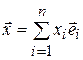 , где
, где  – совокупность базисных векторов, а скаляры xi представляют собой координаты вектора
– совокупность базисных векторов, а скаляры xi представляют собой координаты вектора  = (1, 0, 0, …, 0),
= (1, 0, 0, …, 0),  = (0, 1, 0, …, 0), …,
= (0, 1, 0, …, 0), …,  = (0, 0, …, 0, 1).
= (0, 0, …, 0, 1). ,
,  ,
,  – знак комплексного сопряжения. Свойства: а)
– знак комплексного сопряжения. Свойства: а)  б)
б) 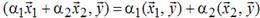 ,
, 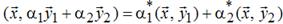 .
. . Док-во: Запишем очевидное неравенство, справедливое для любых векторов
. Док-во: Запишем очевидное неравенство, справедливое для любых векторов 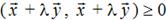 . Раскрывая его, получим
. Раскрывая его, получим  . Поскольку это неравенство справедливо при любых λ, то полагая, что
. Поскольку это неравенство справедливо при любых λ, то полагая, что  , после подстановки и преобразований на основе аксиомы
, после подстановки и преобразований на основе аксиомы  , получаем
, получаем 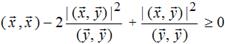 , откуда следует, что
, откуда следует, что 


