
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм нахождения точек экстремума по первому признаку экстремума функции.Содержание книги
Поиск на нашем сайте
· Находим область определения функции. · Находим производную функции на области определения. · Определяем нули числителя, нули знаменателя производной и точки области определения, в которых производная не существует (все перечисленные точки называют точками возможного экстремума, проходя через эти точки, производная как раз может изменять свой знак). · Эти точки разбивают область определения функции на промежутки, в которых производная сохраняет знак. Определяем знаки производной на каждом из интервалов (например, вычисляя значение производной функции в любой точке отдельно взятого интервала). · Выбираем точки, в которых функция непрерывна и, проходя через которые, производная меняет знак - они и являются точками экстремума.
4. первообразная функции, основные свойства первообразных, правила вычисления
Первообрáзной данной функции Первообразные важны тем, что позволяют вычислять интегралы. Если
Это соотношение называется формулой Ньютона — Лейбница Свойства первообразной · Первообразная суммы равна сумме первообразных · Первообразная произведения константы и функции равна произведению константы и первообразной функции · Достаточным условием существования первообразной у заданной на отрезке функции · Пример 1. Доказать, что функция F(x)=15sin5x является первообразной функции f(x)=cos5x. · Для доказательства воспользуемся определением, а точнее тем фактом, что F′(x)=f(x), и найдём производную функции F(x): F′(x)=(15sin5x)′=15⋅5cos5x=cos5x. Значит F(x)=15sin5x является первообразной f(x)=cos5x. Что и требовалось доказать.
5. Таблица первообразных
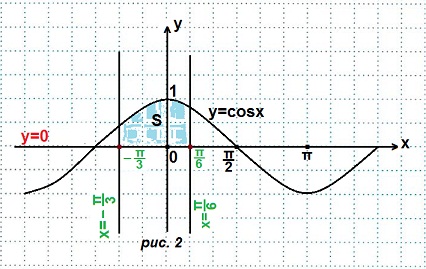
6. Криволинейная трапеция. Площадь криволинейной трапеции Пример 2. Найти площадь криволинейной трапеции, ограниченной линиями:
Решение. Строим графики данных линий. (рис. 2).
Площадь данной криволинейной трапеции:
Криволине́йная трапе́ция — плоская фигура, ограниченная графиком неотрицательной непрерывной функции
Для нахождения площади криволинейной трапеции пользуются интегралом.
7. Вектор, определение, нулевой вектор, длина вектора Определение. Вектор - это направленный отрезок, то есть отрезок, имеющий длину и определенное направление. Графически вектора изображаются в виде направленных отрезков прямой определенной длины. (рис.1)
Обозначение вектора Вектор началом которого есть точка А, а концом - точка В, обозначается AB (рис.1). Также вектора обозначают одной маленькой буквой, например a.
Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|.
Определение. Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают. Нулевой вектор обычно обозначается как 0. Длина нулевого вектора равна нулю. Коллинеарные вектора Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 2).
Сонаправленные вектора Два коллинеарных вектора a и b называются сонаправленными векторами, если их направления совпадают: a↑↑b Противоположно направленные вектора Два коллинеарных вектора a и b называются противоположно направленными векторами, если их направления противоположны: a↑↓b (рис. 4).
Компланарные вектора Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами. (рис. 5).
Всегда возможно найти плоскости параллельную двум произвольным векторам, по-этому любые два вектора всегда компланарные.
Равные вектора Вектора a и b называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны (рис. 6).
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины: a = b, если a↑↑b и |a| = |b|.
Единичный вектор Определение. Единичным вектором или ортом - называется вектор, длина которого равна единице.
8. Нахождение суммы, разности, произведение векторов
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 952; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.76.151 (0.009 с.) |

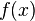 называют такую
называют такую  , производная которой (на всей области определения) равна
, производная которой (на всей области определения) равна 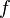 , то есть
, то есть  . Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием
. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием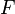 — первообразная интегрируемой функции
— первообразная интегрируемой функции 



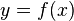 , определенной наотрезке [a; b], осью абсцисс и прямыми
, определенной наотрезке [a; b], осью абсцисс и прямыми  и
и 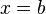 .
.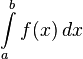
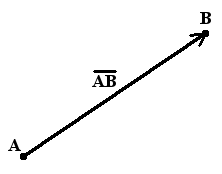


 рис. 4
рис. 4





