
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Численное дифференцирование.Содержание книги
Поиск на нашем сайте
Методы численного дифференцирования применяются, если исходную функцию f(x) трудно или невозможно продифференцировать аналитически. Например, эта функция может быть задана таблично. Задача численного дифференцирования – выбрать легко вычисляемую функцию (обычно полином)
Пусть
В общем случае Оценка погрешности при численном дифференцировании может быть осуществлена по формуле На практике чаще всего используются упрощенные формулы для равномерной сетки, при этом точность нередко повышается. Часто используются следующие формулы для трех узлов:
Исходя из общего вида интерполяционного полинома можно вывести формулы для более высокого порядка точности или для более высоких производных. Численное решение систем линейных уравнений. Классы задач линейной алгебры При численном решении большого круга задач в конечном итоге происходит их линеаризация, в связи с чем в соответствующих алгоритмах весьма широко используются методы линейной алгебры. В их числе:
Постановка задачи решения СЛАУ:
Для решения СЛАУ применяют в основном два класса методов: прямые (выполняемые за заранее известное количество действий) и итерационные (обеспечивающие постепенную сходимость к корню уравнения, зависящую от многих факторов). Прямые методы обычно применяются для решения систем порядка n < 200, для бóльших n используются итерационные методы. Перед решением СЛАУ требуется проанализировать корректную постановку задачи:
1) Если 2) Если
Алгоритм метода Гаусса 1) Прямой ход. Идея метода состоит в последовательном исключении неизвестных из системы n линейных уравнений. На примере первого уравнения системы (2) рассмотрим выражение для x 1:
Подставим выражение для x 1 во второе и все остальные уравнения системы:
Для расширенной матрицы коэффициентов это означает, что каждый элемент первой строки следует поделить на диагональный элемент, а все остальные строки преобразовать, как показано выше. Таким образом, станут равны нулю все коэффициенты первого столбца, лежащие ниже главной диагонали. Затем аналогичная процедура проводится со второй строкой матрицы и нижележащими строками, при этом первая строка и первый столбец уже не изменяются. И так далее до тех пор, пока все коэффициенты, лежащие ниже главной диагонали, не будут равны нулю.
Общие формулы прямого хода:
k = 1… n, j = 1… n +1. Звездочкой отмечены элементы k -й строки с измененными значениями, которые будут подставлены в следующую формулу. Для определенности будем считать первый индекс – по строкам, второй – по столбцам.
i = k +1… n, j = 1… n +1, k фиксировано в уравнении (3). Для уменьшения количества действий достаточно изменять значения элементов, находящихся выше главной диагонали.
2) Обратный ход. Второй этап решения СЛАУ методом Гаусса называется обратным ходом и состоит в последовательном определении x k, начиная с x n, так как для последнего решение фактически получено. Общая формула:
Таким образом, вычисление корней
3) Выбор главного элемента. Для уменьшения погрешности вычислений следует стремиться к тому, чтобы на главной диагонали матрицы стояли максимальные по модулю значения коэффициентов. Алгоритмически этого можно добиться, переставляя строки таким образом, чтобы на диагонали стоял наибольший по модулю элемент текущего столбца. Такая процедура называется выбором главного элемента и осуществляется всякий раз при переходе к новой строке в прямом цикле метода Гаусса.
4) Погрешность метода. Расчет невязок. Точность результатов будет определяться только точностью выполнения арифметических операций при преобразовании элементов матрицы, т.е. ошибкой округления. Контроль правильности полученного решения осуществляется подстановкой полученных значений x 1… x n в исходную систему уравнений и вычислением невязок, т.е. разностей между правыми и левыми частями уравнений:
Специально отметим, что подставлять найденные значения
5) Преимущества и недостатки метода. Преимущество метода в том, что он позволяет достичь результата за заранее известное и фиксированное число действий. Точность результатов будет определяться правильным выбором порядка коэффициентов в матрице
Блок-схема алгоритма метода Гаусса без выбора главного элемента.
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 551; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.7.152 (0.01 с.) |

 , для которой приближенно полагают
, для которой приближенно полагают  .
. Численное дифференцирование – некорректная задача, так как отсутствует устойчивость решения. При численном дифференцировании приходится вычитать друг из друга близкие значения функции. Это приводит к уничтожению первых значащих цифр, т.е. к потере части достоверных знаков числа. А так как значения функции обычно известны с определенной погрешностью, то все значащие цифры могут быть потеряны. На графике кривая (1) соответствует уменьшению погрешности дифференцирования при уменьшении шага; кривая (2) представляет собой неограниченно возрастающий (осциллирующий) вклад неустранимой погрешности исходных данных – значений функции y (x). Критерий выхода за оптимальный шаг при его уменьшении – «разболтка» решения: зависимость результатов вычислений становится нерегулярно зависящей от величины шага.
Численное дифференцирование – некорректная задача, так как отсутствует устойчивость решения. При численном дифференцировании приходится вычитать друг из друга близкие значения функции. Это приводит к уничтожению первых значащих цифр, т.е. к потере части достоверных знаков числа. А так как значения функции обычно известны с определенной погрешностью, то все значащие цифры могут быть потеряны. На графике кривая (1) соответствует уменьшению погрешности дифференцирования при уменьшении шага; кривая (2) представляет собой неограниченно возрастающий (осциллирующий) вклад неустранимой погрешности исходных данных – значений функции y (x). Критерий выхода за оптимальный шаг при его уменьшении – «разболтка» решения: зависимость результатов вычислений становится нерегулярно зависящей от величины шага. , для i = 0,1… n -1, интерполяция полиномом первой степени.
, для i = 0,1… n -1, интерполяция полиномом первой степени. , интерполяция полиномом второй степени.
, интерполяция полиномом второй степени.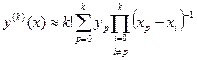 . Минимальное число узлов, необходимое для вычисления k -й производной, равно k + 1.
. Минимальное число узлов, необходимое для вычисления k -й производной, равно k + 1. , где n – число узлов функции, k – порядок производной.
, где n – число узлов функции, k – порядок производной.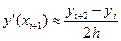 , где h = x 1 – x 0 = const.
, где h = x 1 – x 0 = const. .
.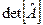 ;
;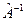 ;
; ;
;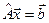 , (1) где
, (1) где  – квадратная матрица коэффициентов размерности n,
– квадратная матрица коэффициентов размерности n,  – вектор неизвестных,
– вектор неизвестных,  – вектор свободных коэффициентов. Иногда СЛАУ представляют в виде расширенной матрицы
– вектор свободных коэффициентов. Иногда СЛАУ представляют в виде расширенной матрицы 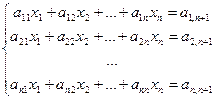 . (2)
. (2) – решение существует и единственно. Если же определитель равен нулю, то тогда, если матрица вырождена (т.е. ее можно преобразовать к виду, когда как минимум одна строка коэффициентов – нули) решений бесконечное множество, иначе решения не существует.
– решение существует и единственно. Если же определитель равен нулю, то тогда, если матрица вырождена (т.е. ее можно преобразовать к виду, когда как минимум одна строка коэффициентов – нули) решений бесконечное множество, иначе решения не существует. .
. .
. .
. , (3)
, (3) , (4)
, (4) . (5)
. (5) , где k = 1… n. (6)
, где k = 1… n. (6)



