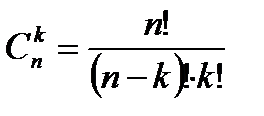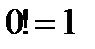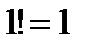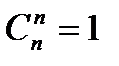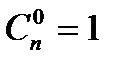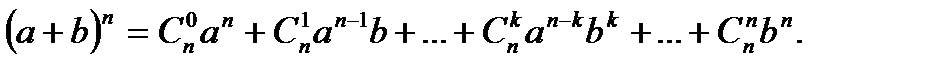Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Знаки тригонометрических функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Sin x cos x tg x ctg x
Простейшие тригонометрические уравнения и частные случаи
Формулы сложения аргументов
Формулы двойного угла
Формулы сложения одноимённых функций
Формулы половинного угла
Преобразование произведения тригонометрических функций в алгебраическую сумму
Производная. Применение производной Таблица производных
Алгоритм составления уравнения касательной к графику функции у = f(х) в точке х = а.
5. Записать получившееся уравнение y = f(a) + f '(а) · (x-a) и привести к виду у = kx+b. Геометрический смысл производной функции у = f(х).
Схема исследования функции 1. Область определения функции 2. Исследование функции на чётность и нечётность: · если · если · если оба условия не выполняются, то функция – ни чётная и ни нечётная 3. Определение точек пересечения с осью х: 4. Определение точек пересечения с осью y: 5. Промежутки возрастания и убывания функции: · находим производную функции · находим критические точки · если · если 6. Точки экстремума: 7. Контрольные точки. 8. Построение графика функции Наибольшее и наименьшее значения функции y = f(x) на отрезке [ а; в ] 1. Область определения функции 2. Находим производную функции 3. Находим критические точки 4. Находим 5. Выбираем из полученных значений наибольшее и наименьшее. 6. Ответ: Степени и корни
Уравнение вида 1. 2. 3. Таблица степеней
Алгоритм решения показательных неравенств
Логарифмы
определение логарифма
основное логарифмическое тождество
Свойства логарифмов 1. 2. 3. 4. 5. 6. 7. 8.
Функции и графики функций Графики известных функций
Графики степенной функции
График показательной функции
График логарифмической функции
График функции вида
Преобразование графика функции y = f(x)
Первообразная и интеграл Таблица первообразных
Неопределенный интеграл Свойства неопределенного интеграла 1. 2. 3. Определенный интеграл
Теория вероятностей и Математическая статистика Факториал Перестановки – комбинация из n элементов по n элементов, где отличается только порядок их следования.
Размещения – из n элементов выбирается k элементов, которые отличаются хотя бы одним элементом или порядком их следования.
Сочетания – число комбинаций из n элементов по k элементов, которые отличаются хотя бы одним элементом, порядок не важен, важен состав.
Бином Ньютона
Треугольник Паскаля
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 545; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |


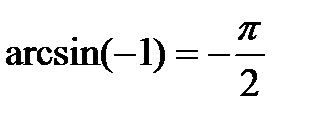
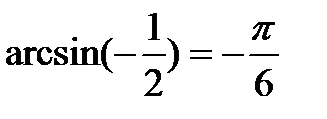



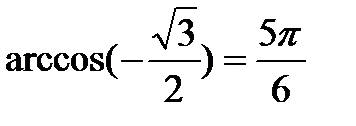

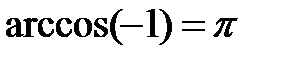
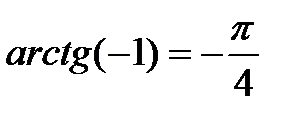

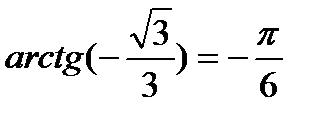


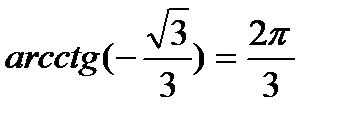
 t = (-1) n arcsin a + πn, n
t = (-1) n arcsin a + πn, n  Частные случаи:
sin t = 1
Частные случаи:
sin t = 1  t =
t =  + 2πn, n
+ 2πn, n  sin t = - 1
sin t = - 1  sin t = 0
sin t = 0 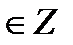
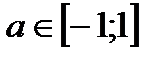 t = ± arccos a + 2πn, n
t = ± arccos a + 2πn, n  cos t = 0
cos t = 0  cos t = 1
cos t = 1 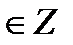
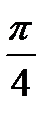 + πn, n
+ πn, n 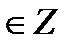 tg t = - 1
tg t = - 1 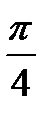 + πn, n
+ πn, n 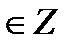 tg t = 0
tg t = 0 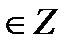
 + πn, n
+ πn, n 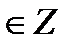 ctg t = - 1
ctg t = - 1 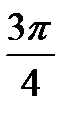 + πn, n
+ πn, n 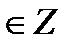 ctg t = 0
ctg t = 0 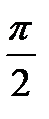 πn, n
πn, n 


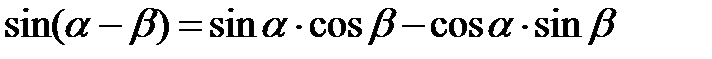



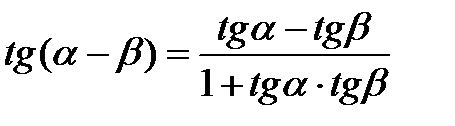


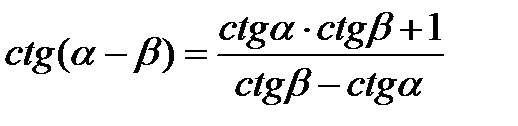
 cosα
cosα
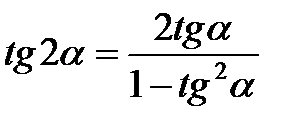

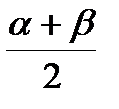 cos
cos 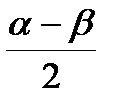
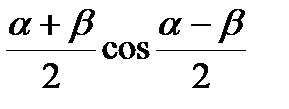
 cos
cos 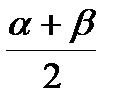



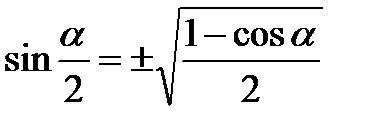
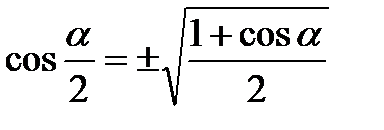
 cos
cos 
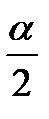 – sin2
– sin2 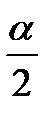

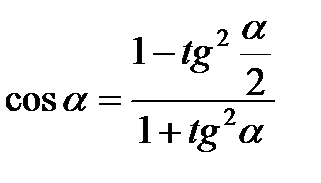
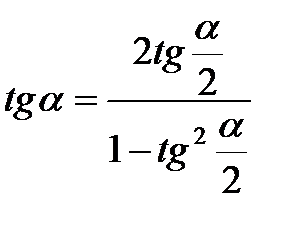
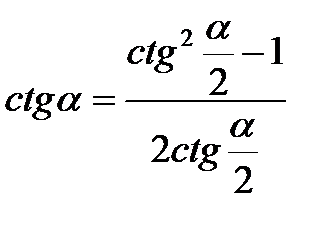
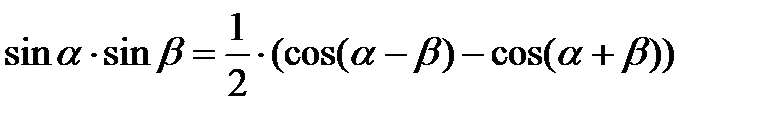
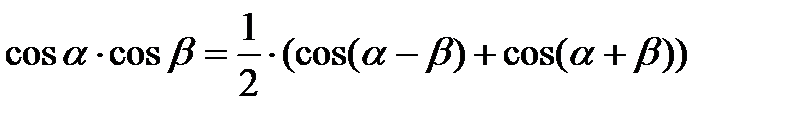

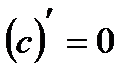



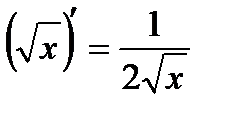




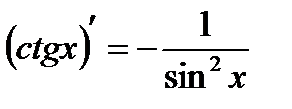
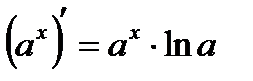


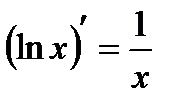
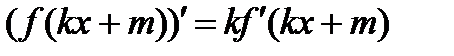 (производная сложной функции)
(производная сложной функции)
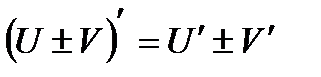
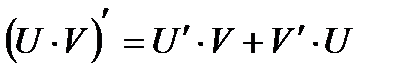

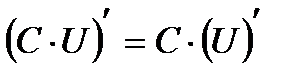
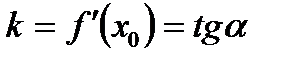 (
( - угловой коэффициент)
- угловой коэффициент)
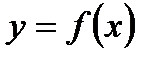 . Обозн.
. Обозн. 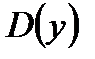
 , то функция чётная
, то функция чётная , то функция нечётная
, то функция нечётная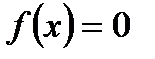
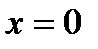 ,
, 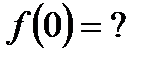
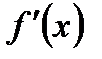

 на промежутке, то функция возрастает на этом промежутке
на промежутке, то функция возрастает на этом промежутке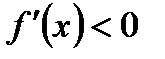 на промежутке, то функция убывает на этом промежутке
на промежутке, то функция убывает на этом промежутке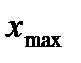 ,
,  .
.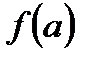 ,
, 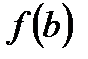 , если
, если 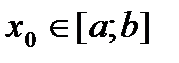 , то находим и
, то находим и 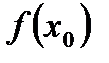 .
.
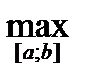
 ;
; 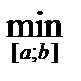
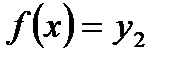 .
.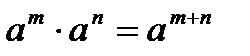

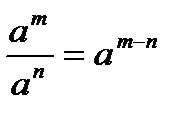

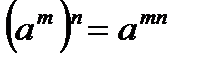

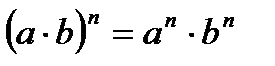
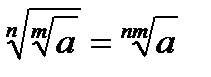
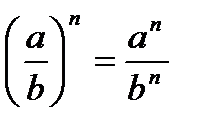
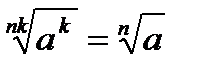
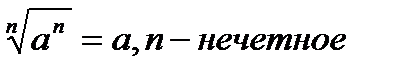 2.
2. 
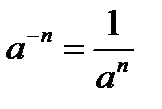
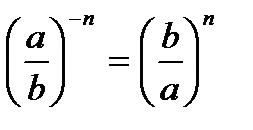
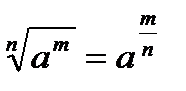


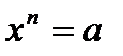 имеет решения:
имеет решения: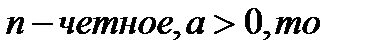
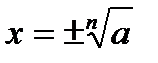
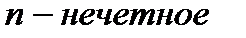 , то
, то 
 корней нет
корней нет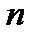

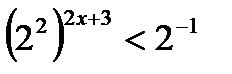
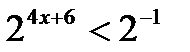
 возрастающая, значит, знакнеравенства сохраняем;
Если 0 < a < 1,то функция
возрастающая, значит, знакнеравенства сохраняем;
Если 0 < a < 1,то функция  возрастающая, значит,
возрастающая, значит,
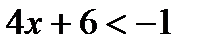
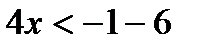
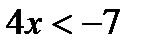

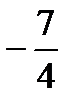
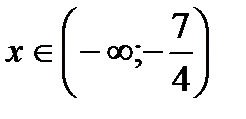
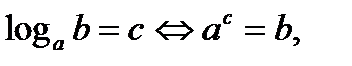 где
где 


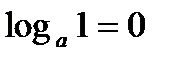

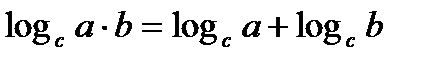
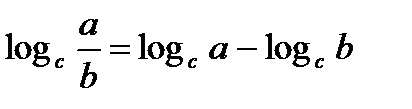

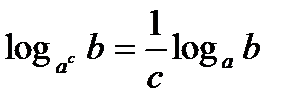

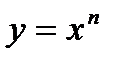
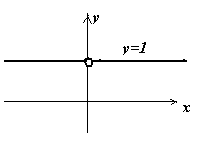
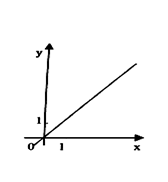

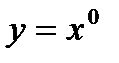
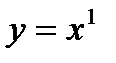


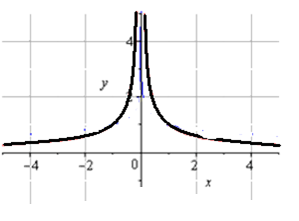

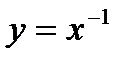

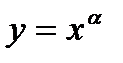 с дробным показателем
с дробным показателем
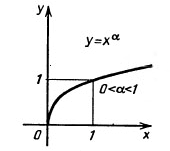

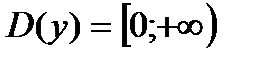
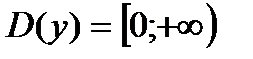
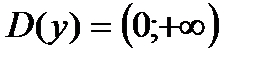

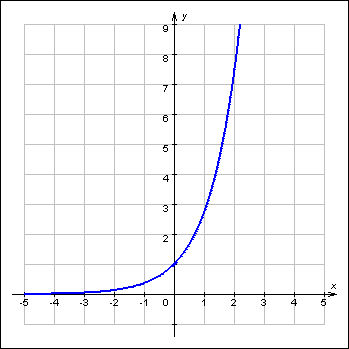

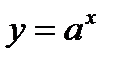 основание а>1, функция возрастающая
основание а>1, функция возрастающая
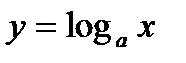
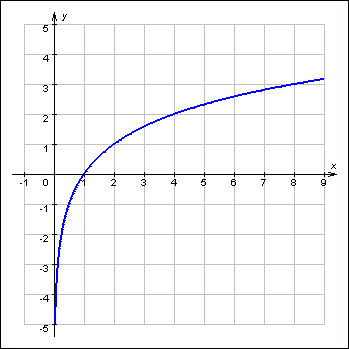

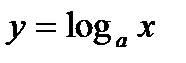 основание а>1, функция возрастающая
основание а>1, функция возрастающая
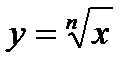
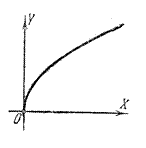
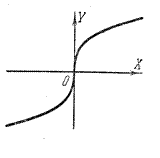
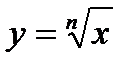 n-чётное
n-чётное
 - функция
- функция
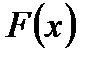 - общий вид первообразных функции
- общий вид первообразных функции

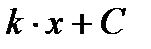
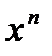
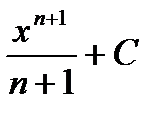

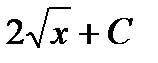
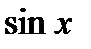
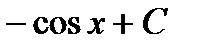


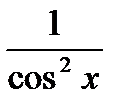
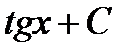

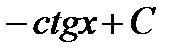


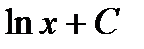

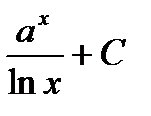

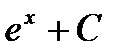

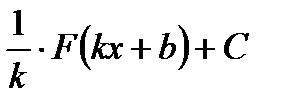
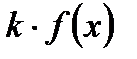

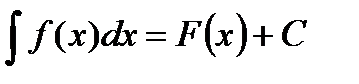 .
.

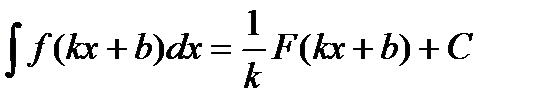
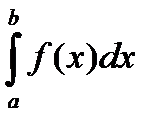 .
.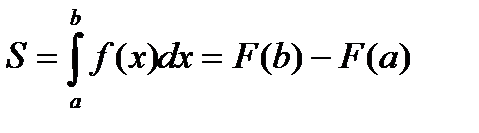
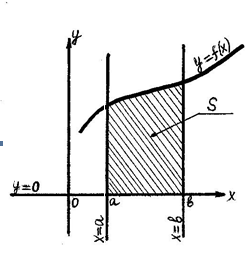
 .
. .
. - с повторениями;
- с повторениями;  - без повторений.
- без повторений.