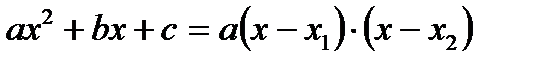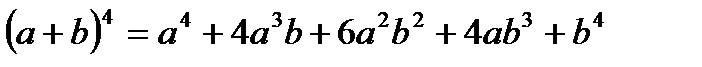Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для профессий и специальностей,Содержание книги
Поиск на нашем сайте
Сборник информационных материалов к программе по дисциплине «Математика» Для профессий и специальностей, подготавливаемых в колледже Г. Череповец Сборник информационных материалов к программе по математике для профессий и специальностей, подготавливаемых в колледже: Пособие по математике для студентов 1 и 2 курсов /Составитель: Ракова А.В., Дедюкова М.Н. - преподаватель математики /- Череповец: Череповецкий химико-технологический колледж, 2013.-33с. Содержание
Аннотация
Сборник информационных материалов предназначен для студентов всех профессий и специальностей, подготавливаемых в колледже. Сборник поможет студентам быстро найти, восстановить в памяти и использовать на практике полученные сведения о том или ином понятии, алгоритме и свойстве, той или иной формуле, что позволит без затруднения решить любой пример или задачу.
Разработчик: Дедюкова Марина Николаевна - преподаватель математики первой квалификационной категории.
Рецензент: Громцева Людмила Алексеевна - преподаватель высшей квалификационной категории, заслуженный учитель РФ.
Рассмотрено и рекомендовано к использованию на заседании ЦМК по ООД № протокола _______ от __________ Председатель _________ (Балдычева О.А.) Пояснительная записка Сборник информационных материалов содержит основной материал по программе «Математика»: математические понятия, формулы, свойства, алгоритмы. В сборнике материал, относящийся к какому-либо понятию, помещен компактно, в одном разделе. Это поможет студентам быстро получить все необходимые сведения об интересующем понятии, таким образом сборник поможет: 1. Быстро найти нужную информацию о том или ином понятии, свойстве, алгоритме, о той или иной формуле; 2. Повторить соответствующий материал при подготовке к уроку, зачету, контрольной работе, экзамену.
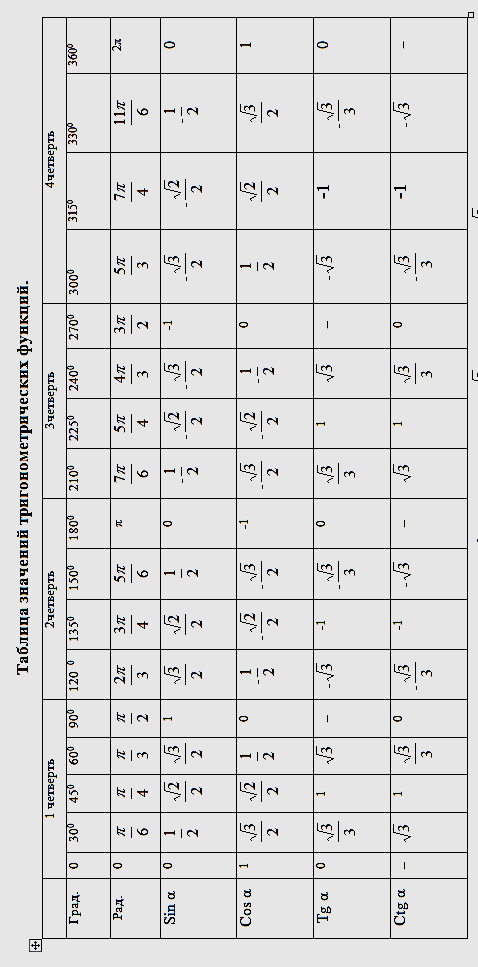
Тригонометрия
Если М(t) = М (х;у), то Основные тождества
Формулы приведения
Макет №1 Макет №2
Знаки тригонометрических функций
Sin x cos x tg x ctg x
Простейшие тригонометрические уравнения и частные случаи
Формулы сложения аргументов
Формулы двойного угла
Формулы половинного угла
Преобразование произведения тригонометрических функций в алгебраическую сумму
Таблица производных
Схема исследования функции 1. Область определения функции 2. Исследование функции на чётность и нечётность: · если · если · если оба условия не выполняются, то функция – ни чётная и ни нечётная 3. Определение точек пересечения с осью х: 4. Определение точек пересечения с осью y: 5. Промежутки возрастания и убывания функции: · находим производную функции · находим критические точки · если · если 6. Точки экстремума: 7. Контрольные точки. 8. Построение графика функции Наибольшее и наименьшее значения функции y = f(x) на отрезке [ а; в ] 1. Область определения функции 2. Находим производную функции 3. Находим критические точки 4. Находим 5. Выбираем из полученных значений наибольшее и наименьшее. 6. Ответ: Степени и корни
Уравнение вида 1. 2. 3. Таблица степеней
Логарифмы
определение логарифма
основное логарифмическое тождество
Свойства логарифмов 1. 2. 3. 4. 5. 6. 7. 8.
Функции и графики функций Графики известных функций
Графики степенной функции
График показательной функции
График логарифмической функции
График функции вида
Преобразование графика функции y = f(x)
Первообразная и интеграл Таблица первообразных
Неопределенный интеграл Теория вероятностей и Математическая статистика Факториал Перестановки – комбинация из n элементов по n элементов, где отличается только порядок их следования.
Размещения – из n элементов выбирается k элементов, которые отличаются хотя бы одним элементом или порядком их следования.
Сочетания – число комбинаций из n элементов по k элементов, которые отличаются хотя бы одним элементом, порядок не важен, важен состав.
Бином Ньютона
Треугольник Паскаля
Теорема Бернулли Пусть
где p – вероятность «успеха», а Уравнения и неравенства
1. Показательное уравнение 2. Логарифмическое уравнение 3. Показательное неравенство вида а) если б) 4. Логарифмическое неравенство вида а) если б) 5. Иррациональное неравенство вида: а) б)
Геометрия Многогранники
Таблица квадратов натуральных чисел от 10 до 99
Список литературы 1. Мордкович А.Г. Алгебра и начала анализа. 10-11 классы. Ч. 1. учебник для общеобразовательных учреждений – М.: Мнемозина,2011. 2. Мордкович А.Г., Суходонский А.М. Справочник школьника по математике,10-11. Алгебра и начала анализа. – М.: Аквариум,1997. 3. Пехлецкий И.Д. Математика: учебник для студентов образовательных учреждений среднего профессионального образования – М.:Академия,2012.
Сборник информационных материалов |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.225.252 (0.008 с.) |

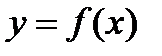 на отрезке
на отрезке 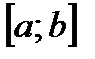

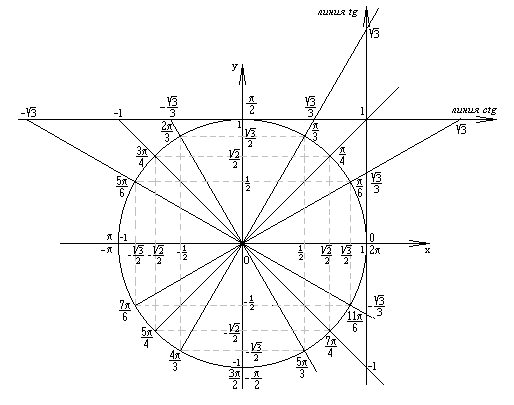
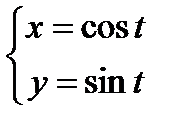 .
.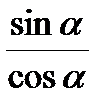
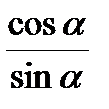
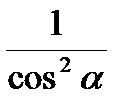
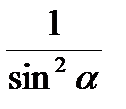
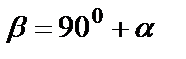
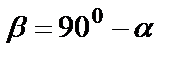
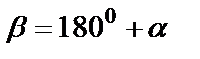
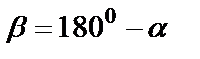
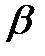
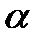
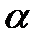

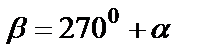
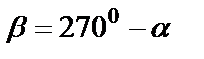
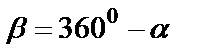
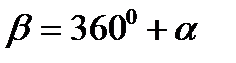

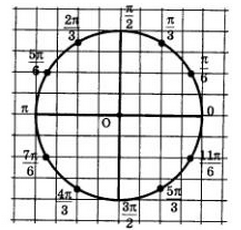

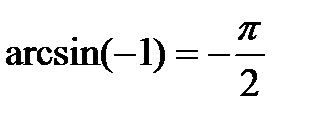
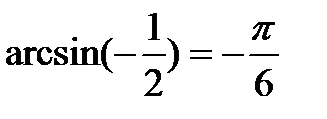



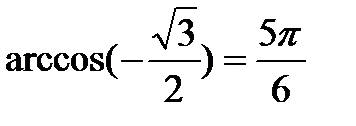

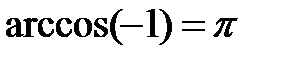
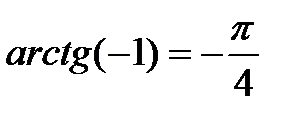

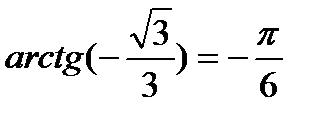


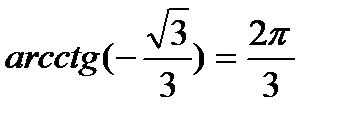
 t = (-1) n arcsin a + πn, n
t = (-1) n arcsin a + πn, n  Частные случаи:
sin t = 1
Частные случаи:
sin t = 1  t =
t =  + 2πn, n
+ 2πn, n  sin t = - 1
sin t = - 1  sin t = 0
sin t = 0 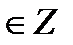
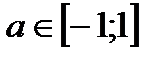 t = ± arccos a + 2πn, n
t = ± arccos a + 2πn, n  cos t = 0
cos t = 0  cos t = 1
cos t = 1 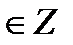
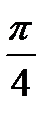 + πn, n
+ πn, n 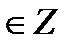 tg t = - 1
tg t = - 1 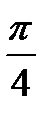 + πn, n
+ πn, n 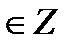 tg t = 0
tg t = 0 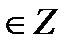
 + πn, n
+ πn, n 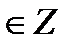 ctg t = - 1
ctg t = - 1 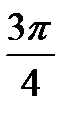 + πn, n
+ πn, n 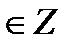 ctg t = 0
ctg t = 0 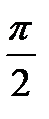 πn, n
πn, n 


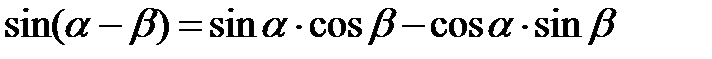



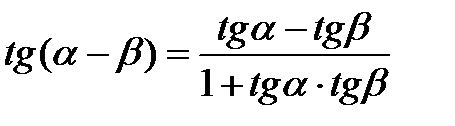


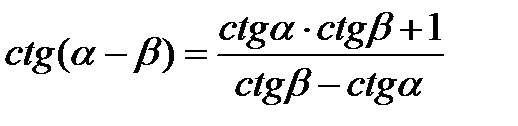
 cosα
cosα
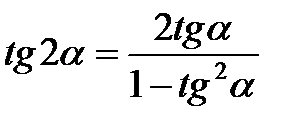

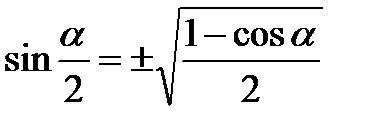
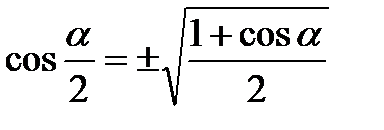
 cos
cos 
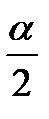 – sin2
– sin2 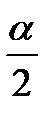

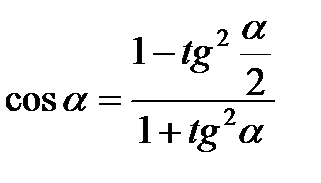
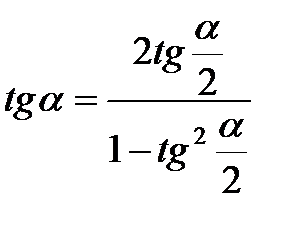
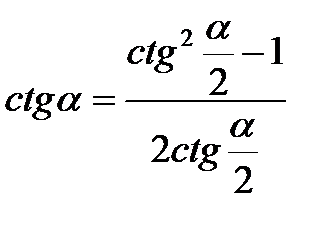
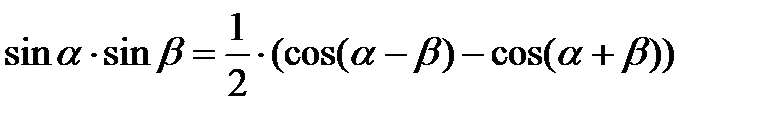
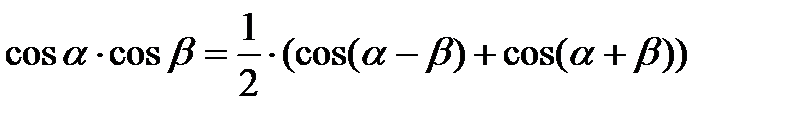

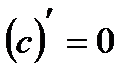



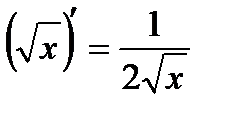




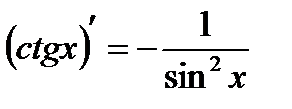
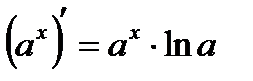


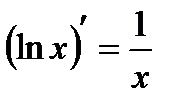
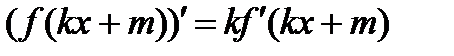 (производная сложной функции)
(производная сложной функции)
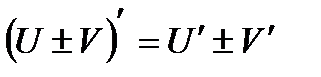
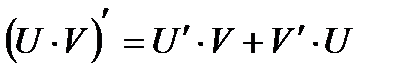

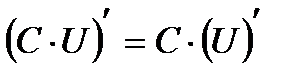
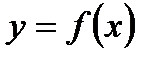 . Обозн.
. Обозн. 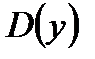
 , то функция чётная
, то функция чётная , то функция нечётная
, то функция нечётная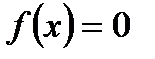
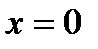 ,
, 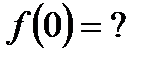
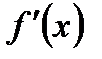

 на промежутке, то функция возрастает на этом промежутке
на промежутке, то функция возрастает на этом промежутке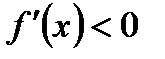 на промежутке, то функция убывает на этом промежутке
на промежутке, то функция убывает на этом промежутке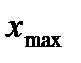 ,
,  .
.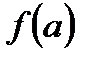 ,
, 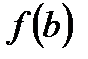 , если
, если 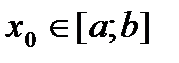 , то находим и
, то находим и 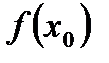 .
.
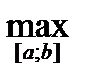
 ;
; 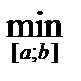
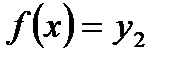 .
.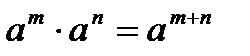

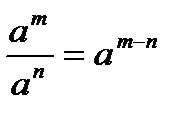

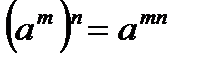

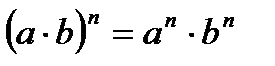
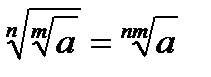
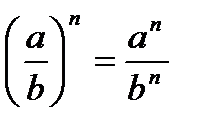
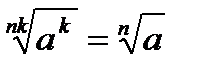
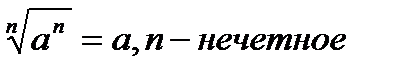 2.
2. 
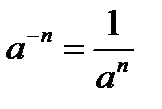
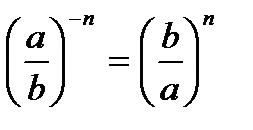
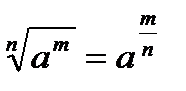


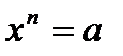 имеет решения:
имеет решения: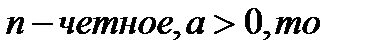
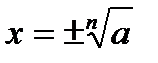
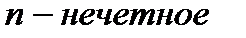 , то
, то 
 корней нет
корней нет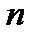
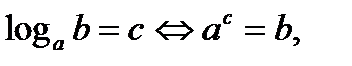 где
где 


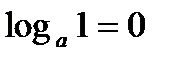

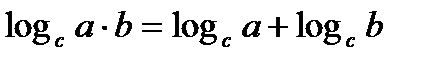
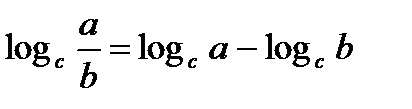

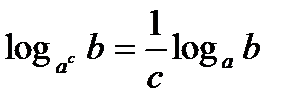

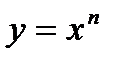
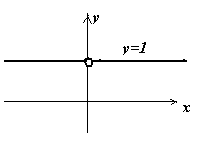
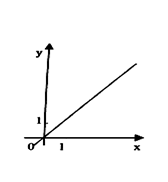

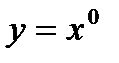
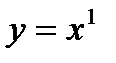


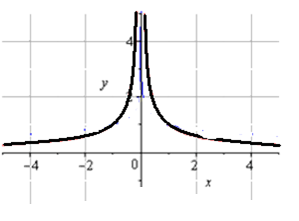

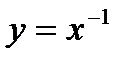

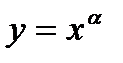 с дробным показателем
с дробным показателем
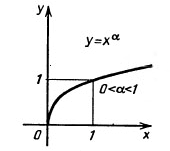

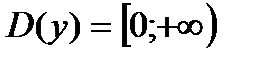
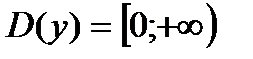
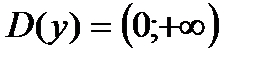

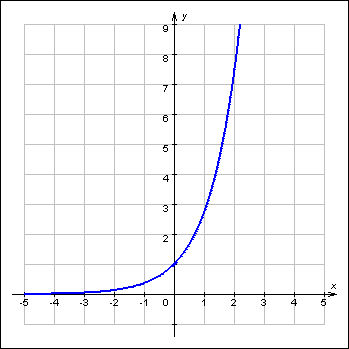

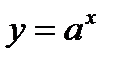 основание а>1, функция возрастающая
основание а>1, функция возрастающая
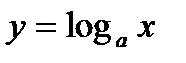
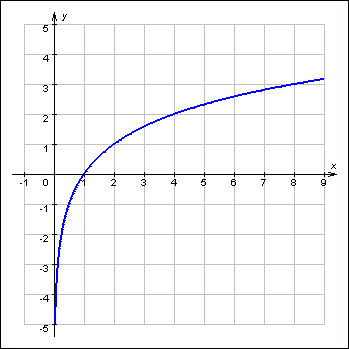

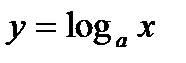 основание а>1, функция возрастающая
основание а>1, функция возрастающая
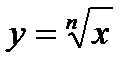
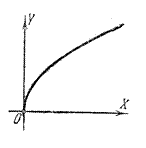
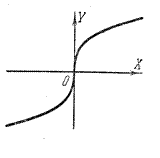
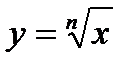 n-чётное
n-чётное
 - функция
- функция
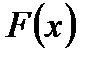 - общий вид первообразных функции
- общий вид первообразных функции

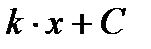
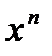
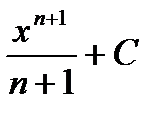

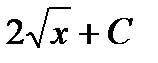
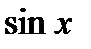
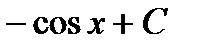


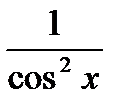
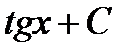

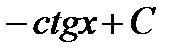


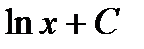

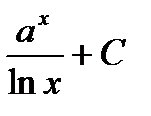

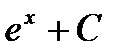

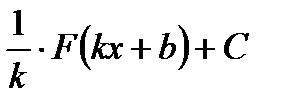
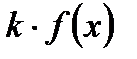

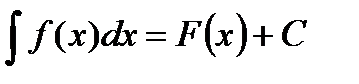 .
. .
. .
. - с повторениями;
- с повторениями;  - без повторений.
- без повторений.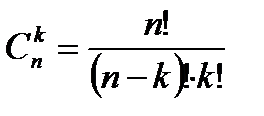
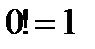
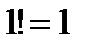
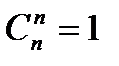
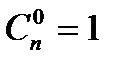
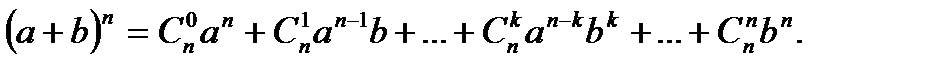

 - вероятность наступления ровно k «успехов» в n независимых повторениях одного и того же испытания. Тогда
- вероятность наступления ровно k «успехов» в n независимых повторениях одного и того же испытания. Тогда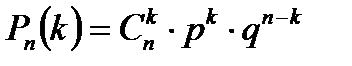 ,
,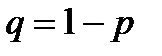 - вероятность «неудачи» в отдельном испытании.
- вероятность «неудачи» в отдельном испытании.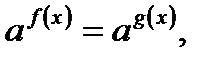 где
где 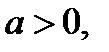
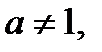 равносильно уравнению
равносильно уравнению 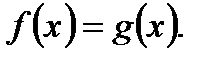
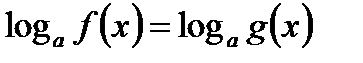 , где
, где  .
. равносильно:
равносильно: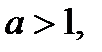 то
то 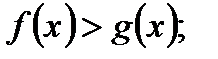
 то
то 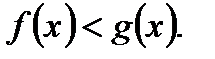
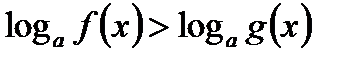 равносильно системе неравенств:
равносильно системе неравенств: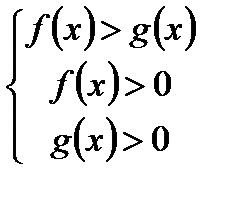 ;
;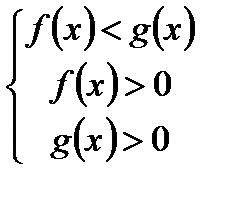 .
. 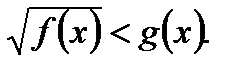 равносильно системе неравенств
равносильно системе неравенств 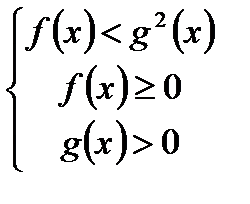 ;
;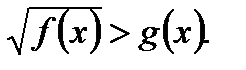 равносильно совокупности систем неравенств
равносильно совокупности систем неравенств 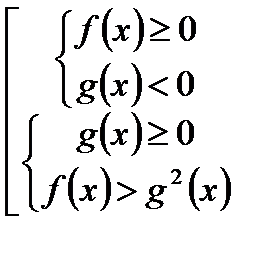
 где
где
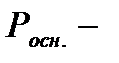 периметр основания,
Н – высота призмы
периметр основания,
Н – высота призмы
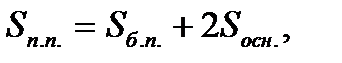
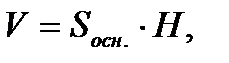 где
где
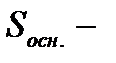 площадь основания,
Н – высота призмы
площадь основания,
Н – высота призмы
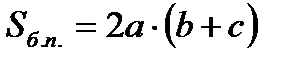
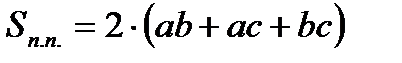
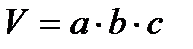

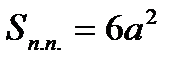
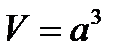

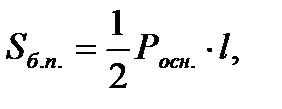 где
где
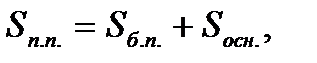
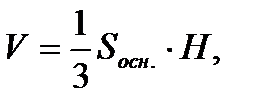 где
где
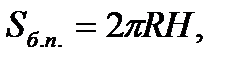 где
R – радиус основания,
Н – высота цилиндра
где
R – радиус основания,
Н – высота цилиндра
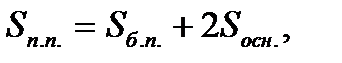 где
где
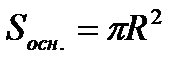
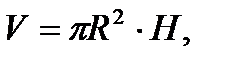
 Конус
Конус
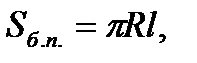 где
R – радиус основания,
l – образующая конуса
где
R – радиус основания,
l – образующая конуса
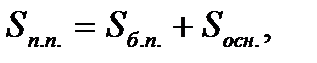 где
где
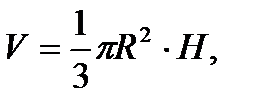 где
H – высота конуса
где
H – высота конуса
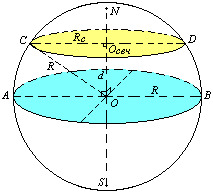
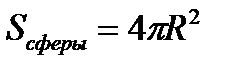
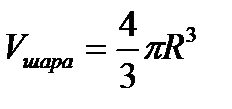
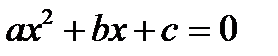
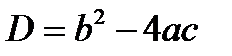 D>0 – два корня:
D>0 – два корня: 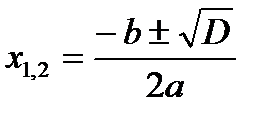 D<0 - нет корней
D=0 – один корень:
D<0 - нет корней
D=0 – один корень: