
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
П. 2 Правила дифференцированияСодержание книги Поиск на нашем сайте
Теорема 1. Пусть 1. 2.
3.
Доказательство:
Докажем третье утверждение данной теоремы. Для этого рассмотрим приращение:
Найдем предел: Теорема 2. Пусть функция Доказательство:
Рассмотрим приращение функции Так как функция
Замечание. Геометрический смысл производной обратной функции (рисунок) Так как Замечание. Если
Теорема 3. Пусть функция Доказательство: По условию функция Найдем предел
Определение 1. Пусть
Теорема 4. Пусть функции Доказательство:
Рассмотрим
Таким образом, Дифференцирование функций, заданных неявно Определение 2. Пусть для каждой точки и Определение 3. Придавая постоянные значения числу z ( Для того, чтобы продифференцировать неявно заданную функцию
Формулы дифференцирования
1)
Доказательство:
Рассмотрим функцию
2) Доказательство:
Рассмотрим функцию 3) Доказательство:
Рассмотрим функцию
4)
Доказательство:
Рассмотрим функцию
5) Доказательство:
Рассмотрим функцию
6)
Доказательство:
Рассмотрим функцию
7)
Доказательство:
Рассмотрим функцию
8) Доказательство:
Рассмотрим функцию 9) 10) 11)
Логарифмическое дифференцирование
Логарифмическое дифференцирование применяется для вычисления производной дробных (целых) выражений, имеющих много скобок и выражений вида
Пример. Вычислим производную функции
Пример. Вычислим производную функции
П. 3 Дифференциал функции
Пусть функция Определение 1. Дифференциалом функции
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 357; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.23.103 (0.007 с.) |

 и
и  - дифференцируемые функции в точке
- дифференцируемые функции в точке  . Тогда:
. Тогда: ;
;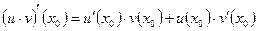 ;
; , причем
, причем  в некоторой окрестности точки
в некоторой окрестности точки  .
.
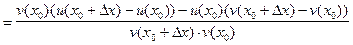 .
.
 . Таким образом,
. Таким образом, 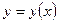 дифференцируема в точке
дифференцируема в точке  ). Тогда обратная функция
). Тогда обратная функция  , причем
, причем  .
. . Тогда
. Тогда  .
. дифференцируема в точке
дифференцируема в точке  соответствует малое приращение функции
соответствует малое приращение функции  . ■
. ■ , где
, где  - угол наклона касательной, проведенной к графику функции
- угол наклона касательной, проведенной к графику функции  .
. растет быстрее
растет быстрее  в
в  раз, то
раз, то  раз.
раз. дифференцируема в некоторой точке
дифференцируема в некоторой точке  , а функция
, а функция  дифференцируема в точке
дифференцируема в точке  дифференцируема в точке
дифференцируема в точке  .
. дифференцируема в точке
дифференцируема в точке  . Тогда, используя дифференцируемость функции
. Тогда, используя дифференцируемость функции  , получим
, получим  . Подставим
. Подставим  в
в  :
:  .
. . ■
. ■ . Говорят, что линия на плоскости задана параметрически, если ее точки имеют координаты
. Говорят, что линия на плоскости задана параметрически, если ее точки имеют координаты  . Таким образом, параметрическое задание данной линии
. Таким образом, параметрическое задание данной линии  равносильно ее явному заданию
равносильно ее явному заданию  .
. дифференцируема в точке
дифференцируема в точке  .
. ,
, . По условию функция
. По условию функция  соответствует бесконечно малое
соответствует бесконечно малое  . ■
. ■ плоскости
плоскости  существует единственное число
существует единственное число  . Тогда говорят, что на плоскости задана функция
. Тогда говорят, что на плоскости задана функция  двух переменных
двух переменных  .
. ), получим уравнения, задающие линии в пространстве. Тогда функция
), получим уравнения, задающие линии в пространстве. Тогда функция  , называется заданной неявно.
, называется заданной неявно. , то уравнение
, то уравнение  задает окружности с центром на оси
задает окружности с центром на оси  . Найдем производную функции
. Найдем производную функции  .
.
 . Так как
. Так как , то
, то
 . Для доказательства этой формулы мы воспользовались следствием 4 из второго замечательного предела. ■
. Для доказательства этой формулы мы воспользовались следствием 4 из второго замечательного предела. ■ .
. . Так как
. Так как 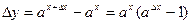 , то
, то  . Для доказательства этой формулы мы воспользовались следствием 4 из второго замечательного предела. ■
. Для доказательства этой формулы мы воспользовались следствием 4 из второго замечательного предела. ■ .
. . Так как
. Так как  , то
, то . Для доказательства этой формулы мы воспользовались следствием 3 из второго замечательного предела. ■
. Для доказательства этой формулы мы воспользовались следствием 3 из второго замечательного предела. ■ .
. . Так как
. Так как , то
, то  . Для доказательства этой формулы мы воспользовались первым замечательным пределом и непрерывностью функции
. Для доказательства этой формулы мы воспользовались первым замечательным пределом и непрерывностью функции  . ■
. ■ .
. , то
, то . Для доказательства этой формулы мы воспользовались первым замечательным пределом и непрерывностью функции
. Для доказательства этой формулы мы воспользовались первым замечательным пределом и непрерывностью функции  .
. . Используя правила дифференцирования, получим
. Используя правила дифференцирования, получим . ■
. ■ .
. . Используя правила дифференцирования, получим
. Используя правила дифференцирования, получим
 ■
■ .
. . Используя правила дифференцирования, получим
. Используя правила дифференцирования, получим  . ■
. ■ .
. .
. .
. . Для начала необходимо прологарифмировать выражение, затем взять производную от обеих частей, учитывая, что
. Для начала необходимо прологарифмировать выражение, затем взять производную от обеих частей, учитывая, что  :
: ,
, .
. :
: ,
, ,
, .
. дифференцируема в точке
дифференцируема в точке  , тогда
, тогда  ,
,  .
. называется главная часть приращения и обозначается.
называется главная часть приращения и обозначается.  . Дифференциалом аргумента (вне зависимости от переменной) называют его приращение
. Дифференциалом аргумента (вне зависимости от переменной) называют его приращение  . Таким образом, дифференциал функции равен
. Таким образом, дифференциал функции равен  . Тогда производная функции равна
. Тогда производная функции равна 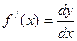 .
.


