
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
для различных видов правых частейСодержание книги Поиск на нашем сайте
Таблица 3.1
Здесь Пример 3.15. Найти общее решение уравнение Решение. Общее решение неоднородного линейного уравнения:
Приравниваем коэффициенты при одинаковых степенях
откуда Общее решение исходного уравнения будет
Пример 3.15. Найти общее решение системы дифференциальных уравнений
Решение. Дифференцируя одно из уравнений системы по Итак,
Из второго уравнения находим
Наконец, найдем
После преобразования получаем однородное уравнение второго порядка с постоянными коэффициентами:
Решая характеристическое уравнение
Функцию
Контрольная работа №4. «Интегральное исчисление функции одной независимой переменной» Задача 1. Вычислить неопределенные интегралы
Задача 2. Вычислить неопределенные интегралы
Задача 3. Вычислить площадь фигур, ограниченных графиками функций
Задача 4. Вычислить длину дуги кривой, заданной параметрическими уравнениями (для 1-14 вариантов)
Вычислить длину дуги кривой, заданной уравнением в полярных координатах (для 15-30 вариантов)
Контрольная работа №5. «Дифференциальное исчисление функций многих переменных» Задача 1. Найти область определения указанных функций.
Задача 2. Найти частные производные первого порядка функции
Задача 3. Найти градиент функции
Задача 4. Найти частные производные второго порядка функции
Задача 5. Проверить, удовлетворяет ли указанному уравнению данная функция
Задача 6. Найти экстремум функции
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 388; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.215.5 (0.009 с.) |



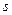


 не является корнем характеристического уравнения
не является корнем характеристического уравнения



 не являются корнями характеристического уравнения
не являются корнями характеристического уравнения




 не являются корнями характеристического уравнения
не являются корнями характеристического уравнения


 - многочлены от
- многочлены от 
 -й степени общего вида с неопределенными коэффициентами.
-й степени общего вида с неопределенными коэффициентами. .
. . Соответствующее однородное уравнение имеет вид:
. Соответствующее однородное уравнение имеет вид:  . Составим характеристическое уравнение
. Составим характеристическое уравнение  . Его корни
. Его корни  ,
,  . В силу формулы (3.16)
. В силу формулы (3.16)  . Частное решение неоднородного уравнения будем искать в виде
. Частное решение неоднородного уравнения будем искать в виде  (см. таблицу 3.1). Находим производные и подставляем в заданное уравнение:
(см. таблицу 3.1). Находим производные и подставляем в заданное уравнение: ,
,  ,
, ,
,  .
. ,
, ,
,  ,
,  .
. .
. .
. (например, первое уравнение) и исключая функцию
(например, первое уравнение) и исключая функцию  , сведем уравнение системы к решению уравнения второго порядка с постоянными коэффициентами. Решая это уравнение, найдем функцию
, сведем уравнение системы к решению уравнения второго порядка с постоянными коэффициентами. Решая это уравнение, найдем функцию 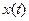 , а затем из первого уравнения найдем и функцию
, а затем из первого уравнения найдем и функцию  .
. .
.
 и подставим в уравнение (3.19):
и подставим в уравнение (3.19):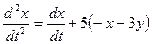 ;
;  .
. ,
,
 .
. .
. , получим
, получим  , откуда
, откуда .
. в формулу (3.20), после преобразований получим
в формулу (3.20), после преобразований получим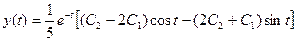 .
.














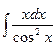


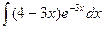







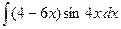
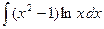


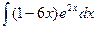

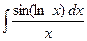


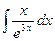



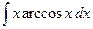

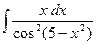


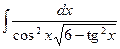

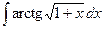
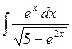
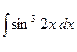


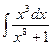


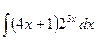


















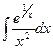
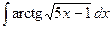












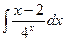
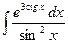


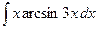
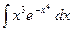





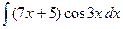


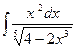


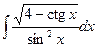












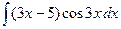
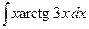






























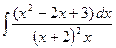






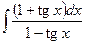













































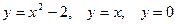




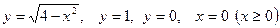


 .
.

 .
.

 .
.

 .
.


 .
.

 .
.


 ,
,  ,
, 
 .
.
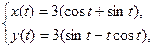

 ,
,  .
.
 ,
,  .
.
 ,
,  .
.
 ,
,  .
.
 ,
,  .
.
 ,
,  .
.
 ,
,  .
.
 ,
,  ,
,  .
.
 ,
,  ,
,  .
.
 ,
,  .
.
 ,
,  ,
, 















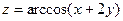

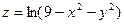





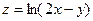





 .
.
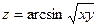








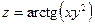



















 в точке
в точке  . Вычислить производную по направлению вектора
. Вычислить производную по направлению вектора  от функции
от функции  .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.

 .
.

 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
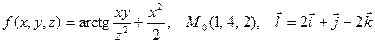 .
.
 .
.
 .
.
 .
.


 .
.










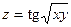










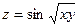






 .
. .
.
 .
.
 .
.
 .
.
 .
.


 .
.

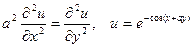 .
.
 .
.
 .
.


 .
.
 .
.

 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.


















