
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование тригонометрических функций.Содержание книги Поиск на нашем сайте
Интегралы вида
Пример 1.18. Вычислить Решение. Подынтегральная функция является рациональной относительно
Замечание 1.3. Универсальная подстановка В некоторых частных случаях нахождение интегралов вида 1. Если 2. Если 3. Если Пример 1.19. Вычислить Решение. Подынтегральная функция четна относительно синуса и косинуса. Полагаем
Далее имеем
Заметим, что нахождение интеграла можно упростить, если в исходном интеграле разделить числитель и знаменатель на
Интегралы вида Случай 1. По крайней мере один из показателей Если Пример 1.20. Вычислить Решение. Полагая
Случай 2. Оба показателя
Пример 1.21. Вычислить Решение. Из формулы (1.4) следует, что
Применив теперь формулу (1.5), получим
Итак,
Интегрирование иррациональных функций. Интегралы вида Пример 1.22. Вычислить Решение. Здесь
Интегралы вида Пример 1.23. Вычислить Решение. Положим
Выразим
Окончательно получаем
Определенный интеграл Основные свойства определенного интеграла 1. 2. 3. 4. 5. Правила вычисления определенных интегралов 1. Формула Ньютона-Лейбница:
где 2. Интегрирование по частям:
где 3. Замена переменной:
где 3. Если
4. Если
Пример 1.24. Вычислить Решение. По формуле Ньютона-Лейбница имеем
Пример 1.25. Вычислить Решение. Воспользуемся методом интегрирования по частям. Положим
Пример 1.26. Вычислить Решение. Положим
Приложение определенного интеграла Приведем некоторые приложения определенного интеграла. Вычисление площади плоской фигуры Площадь криволинейной трапеции, ограниченной кривой
Площадь фигуры, ограниченной кривыми
Если кривая задана параметрическими уравнениями
где Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением
Пример 1.27. Вычислить площадь фигуры, ограниченной параболой
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 511; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.241.205 (0.006 с.) |

 , где
, где  - рациональная функция. Интегралы указанного вида приводят к интегралам от рациональных функций с помощью так называемой универсальной тригонометрической подстановки
- рациональная функция. Интегралы указанного вида приводят к интегралам от рациональных функций с помощью так называемой универсальной тригонометрической подстановки  . В результате этой подстановки имеем:
. В результате этой подстановки имеем: ,
, 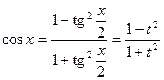 ,
,  ,
, 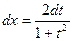 .
. .
.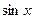 и
и  . Воспользуемся подстановкой
. Воспользуемся подстановкой 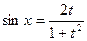 ,
, 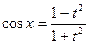 ,
, 
 во многих случаях приводит к сложным вычислениям.
во многих случаях приводит к сложным вычислениям. , то интеграл рационализируется подстановкой
, то интеграл рационализируется подстановкой  .
. , то интеграл рационализируется подстановкой
, то интеграл рационализируется подстановкой  .
. , то интеграл рационализируется подстановкой
, то интеграл рационализируется подстановкой  (или
(или 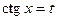 ).
). .
. ,
,  ,
,  ,
,  . Отсюда получаем
. Отсюда получаем .
.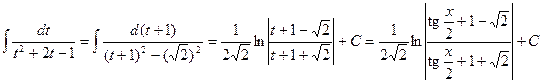 .
. :
: .
. . Выделим здесь два случая.
. Выделим здесь два случая. или
или  - нечетное положительное число.
- нечетное положительное число. .
. , получим
, получим
 .
. ,
,
 ,
,

 .
. .
. .
. .
. , где
, где  - целые числа. С помощью подстановки
- целые числа. С помощью подстановки  , где
, где 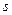 - наименьшее общее кратное чисел
- наименьшее общее кратное чисел  , заданный интеграл преобразуется в интеграл от рациональной функции.
, заданный интеграл преобразуется в интеграл от рациональной функции. .
. поэтому
поэтому  . Воспользуемся подстановкой
. Воспользуемся подстановкой  , тогда
, тогда 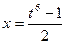 ,
,  и, следовательно,
и, следовательно,
 .
. ,
,  ,
,  приводят к интегралам от
приводят к интегралам от  ,
, 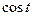 функции с помощью соответствующей замены: для первого интеграла
функции с помощью соответствующей замены: для первого интеграла  (или
(или  ), для второго
), для второго  (или
(или  ) и для третьего
) и для третьего  (или
(или  ).
). .
.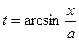 ,
,  . Подставляя в исходный интеграл, получим
. Подставляя в исходный интеграл, получим .
. , если
, если  ,
, .
. .
. .
. .
. .
. .
. , где
, где 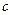 - постоянная.
- постоянная. ,
, непрерывна на отрезке
непрерывна на отрезке  ,
, 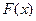 - первообразная для
- первообразная для  ,
, ,
, 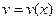 - непрерывно дифференцируемые функции на отрезке
- непрерывно дифференцируемые функции на отрезке  ,
,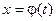 - непрерывная вместе со своей производной
- непрерывная вместе со своей производной  на отрезке
на отрезке  ,
,  ,
, 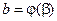 ,
,  - функция, непрерывная на
- функция, непрерывная на 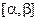 .
. , то
, то .
. , то
, то .
.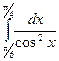 .
. .
. .
. ,
, 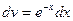 , откуда
, откуда  ,
, 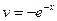 . Тогда получим
. Тогда получим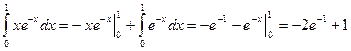 .
. .
. , тогда
, тогда  ; если
; если 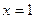 , то
, то  ; если
; если  , тогда
, тогда 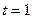 . Следовательно,
. Следовательно, .
. (где
(где  ), прямыми
), прямыми  ,
,  и отрезком
и отрезком  , вычисляется по формуле
, вычисляется по формуле .
.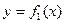 и
и 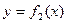 (где
(где  ),прямыми
),прямыми  .
.
 , то площадь криволинейной трапеции, ограниченной этой кривой, прямыми
, то площадь криволинейной трапеции, ограниченной этой кривой, прямыми  ,
, и
и  определяются из уравнений
определяются из уравнений 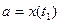 ,
, 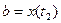 , а
, а  при
при  .
. и двумя полярными радиусами
и двумя полярными радиусами  ,
,  (
( ), находится по формуле
), находится по формуле .
. и прямой
и прямой  (рис 1.1).
(рис 1.1).
 ,
,  .
Откуда
.
Откуда 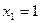 ,
,  . Тогда по формуле (1.6) имеем
. Тогда по формуле (1.6) имеем
 .
.
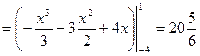 .
.



