
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Роль и место тригонометрических уравнений в школьном курсе математикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Тригонометрические уравнения занимают одно из центральных мест в курсе математики средней школы, как по содержанию учебного материала, так и по способам учебно-познавательной деятельности. Умения решать тригонометрические уравнения должны быть сформированы при их изучении и применены к решению большого числа задач теоретического и прикладного характера. В школьном математическом образовании с изучением тригонометрических уравнений связаны несколько направлений: -прикладная направленность; -теоретико-математическая направленность; -направленность на установление связей с остальным содержанием математики Требованием нашего времени является необходимость усиления прикладных направлений в обучении математике. Как показал анализ содержания школьного математического образования, возможности решения тригонометрических уравнений в этом плане достаточно широки. Тригонометрия традиционно является одной из важнейших составных частей школьного курса математики. И этот курс предполагает задачи, решить которые, как правило, можно, пройдя целенаправленную специальную подготовку. Анализ школьных учебников по математике в полной степени определяет место тригонометрических уравнений в линии изучения уравнений. Изучению темы «Решение тригонометрических уравнений» часто предшествует изучение таких тем как «Преобразование тригонометрических выражений» и «Основные свойства и графики тригонометрических функций». В разделе «Решение тригонометрических уравнений и неравенств» мы знакомим учащихся с понятиями арксинус, арккосинус, арктангенс. Опыт преподавания математики показывает, что осознание важности изучаемого материала приходит к ученикам не в процессе его изучения, а в процессе его применения при решении других заданий, т.е. тогда когда он становится средством для решения других задач. Так, например, решение уравнения При таком подходе изучения тригонометрии, когда уравнения и неравенства изучаются после формул преобразования тригонометрических выражений, место тригонометрических уравнений и неравенств определяется через систематизацию знаний по темам «Преобразование тригонометрических выражений» и «Основные свойства и графики тригонометрических функций». Если же тригонометрические уравнения и неравенства изучаются до темы «Преобразование тригонометрических выражений», то здесь место их изучения определяется совершенно противоположным образом. Здесь на изучение тригонометрических уравнений отводится больше времени: как только появляется новая формула, она сразу же используется для решения уравнений или неравенств. То есть в данном случае не формула преобразования является средством для решения тригонометрического уравнения или неравенства, а уравнение выступает как средство закрепления тригонометрических формул. Учебник Мордкович А.Г. Алгебра и начала анализа. 10-11 разбит на 8 глав. В конце изучения каждой главы чётко обозначены основные результаты изучения. Курс изучения математики в 10 классе начинается с изучения главы «Тригонометрические функции». Здесь автор вводит понятия тригонометрической окружности на координатной плоскости, понятия синус и косинус, основные тригонометрические соотношения с ними связанные, решения простейших уравнений по тригонометрической окружности. Как таковые формулы приведения вводятся после изучения тригонометрических функций углового аргумента. Далее рассматриваются свойства и графики тригонометрических функций. Во второй главе «Тригонометрические уравнения» подробно рассматривается решение каждого простейшего тригонометрического уравнения, на основе ранее введенных понятий арксинуса, арккосинуса, арктангенса. В этой же главе рассмотрены такие методы решения: разложение на множители и введение новой переменной; метод решения однородных тригонометрических уравнений. Другие методы решения рассматриваются после изучения третьей главы «Преобразование тригонометрических выражений». Здесь схема изучения выглядит следующим образом: функция → уравнения → преобразования. С точки зрения применения учебник Мордковича удобен для самостоятельного изучения учащимися, т.к. он содержит сильную теоретическую базу. Изложение теоретического материала ведётся очень подробно. В условиях острой нехватки часов для проведения занятий в классе возрастает значение самостоятельной работы учеников с книгой. Опираясь на учебник, учитель прекрасно разберётся в том, что надо рассказать учащимся на уроке, что заставить их запомнить, а что предложить им просто прочесть дома. К недостаткам можно отнести не очень большое количество упражнений по этой теме в самом учебнике. Таким образом, при любом подходе к изучению тригонометрии, роль изучения уравнений и неравенств неизмеримо велика, не зависимо от места их изучения. Ну и как следствие из этого велико и неизмеримо место изучения методов решения и тригонометрических уравнений. Т.к. авторы учебников не уделяют должного внимания обозначению методов решения тригонометрических уравнений и неравенств, попробуем классифицировать уравнения и неравенства, и соответственно методы их решения.
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 761; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.216.248 (0.007 с.) |

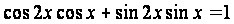 , сводится к простейшему уравнению
, сводится к простейшему уравнению  , причём частному виду простейшего, после элементарного преобразования выражения, стоящего в левой части уравнения по формулам сложения косинуса. Мы видим, что именно здесь школьники могут наблюдать пользу от изучения формул тригонометрии. С их помощью нерешаемое, на первый взгляд, уравнение принимает достаточно простой и, главное знакомый вид.
, причём частному виду простейшего, после элементарного преобразования выражения, стоящего в левой части уравнения по формулам сложения косинуса. Мы видим, что именно здесь школьники могут наблюдать пользу от изучения формул тригонометрии. С их помощью нерешаемое, на первый взгляд, уравнение принимает достаточно простой и, главное знакомый вид.


