
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Целые и рациональные числа. Действия с целыми и рациональными числами.Содержание книги
Поиск на нашем сайте
Целые и рациональные числа. Действия с целыми и рациональными числами. Целые числа – это числа из множества {0, 1, -1, 2, -2,....}. Это множество состоит из трех частей – натуральные числа, отрицательные целые числа (противоположные натуральным числам) и число 0 (нуль). Целые числа обозначаются латинской буквой Z. Можно сказать, что Z ={1,2,3,....}. Рациональные числа – это числа, представимые в виде дроби Действительные числа. Действительные (вещественные) числа – это числа, которое применяются для измерения непрерывных величин. Множество действительных чисел обозначается латинской буквой R. Действительные числа включают в себя рациональные числа и иррациональные числа. Иррациональные числа – это числа, которые получаются в результате выполнения различных операций с рациональными числами (например, извлечение корня, вычисление логарифмов), но при этом не являются рациональными. Примеры иррациональных чисел – это Комплексные числа. Работа с комплексными числами. Комплексным числом называются числа вида a+bi, где а и b – действительные числа, i – мнимая единица (i2 =-1) Два числа a1 +b1i и a2 + b2i называются равными, если a1= a2, b1= b2 Сумма двух комплексных чисел называется комплексное число, равное a1+ b1i+ a2+ +b2i= a1+ a2+i(b1+ b2) Разностью двух комплексных чисел называется комплексное число вида (a1 +b1i)- -(a2- b2i) Произведением двух комплексных чисел называется комплексное число, равное (a1+ +b1i)(a2 + b2i)= a1a2+ a1b2i + a2b1i + b1b2i2=(a1a2- b1b2)+i(a1b2+ a2b1) Запись комплексного числа в виде z= a+bi называется алгебраической формой записи комплексного числа, где а-действительное число, bi-мнимая часть
Функции и графики. Функция – числовой функцией с областью определения Д называются соответствие, при котором каждому числу х из множества Д сопоставляется по некоторому правилу число у, зависящее от х. х-независимая переменная или аргумент функции; у-соответствует числу х, называется значением функции f в точке х, обозначают y=f(x) Область определения функции f обозначается D(f). Множество, состоящее из всех чисел f(x), таких что х принадлежит области определения функции f, называют областью значения функции f и обозначают E(f). Функции вида f(x)=p(x), где p(x) – многочлен, называют целыми рациональными функциями, а функцию вида f(x)=q(x)p(x) , где p(x) и q(x) – многочлены, называют дробно-рациональными функциями, q(x) не равно 0, т.е область определения дробно-рациональной функции – множество всех чисел R, из которых исключены корни многочлена q(x) Графиком функции f называют множество всех точек (х;у) координатной плоскости, где у=f(x), а х «пробегает» всю область определения функции f/ y=ax2+bx+c, где b отвечает за ось х: b>0 –влево; b<0 -вправо, с – за ось у: с>0 –вверх; c<0-вниз, |a|>1-сужается, а 0<|a|<1 -расширяется Четные и нечетные функции. Определение четных и нечетных функций. Функция называется четной, если для любого х из её области определения f(-x)=f(x) Функция называется нечетной, если для любого х из её области определения f(-x)=-f(x) Свойства: 1. график четн функции симметричен относительно ардинат ОХ 2. график нечетн функции симметричен относительно начала координат При построенрии графика четн или нечетн функции достаточно построить его часть для неотрицательных х, а затем отразить полученный график относительно оси ардинат(в случае четн) или начала координат(в случае нечетн) Определение тригонометрических функций. Синус, - отношение катета, лежащего против этого угла, к гипотенузе. КО́СИНУС - катета, прилегающего к острому углу в прямоугольном треугольнике, к гипотенузе. ТА́НГЕНС - отношение катета, лежащего против острого угла в прямоугольном треугольнике, к другому катету КОТА́НГЕНС отношение катета, прилегающего к острому углу в прямоугольном треугольнике, к другому катет. Синус отвечает за ось у, а косинус за ось х Основные тождества тригонометрии. Формулы сложения. Формулы сложения
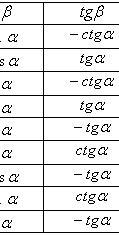
Формулы приведения
Формулы двойного угла
Формулы половинных углов
16. Свойства и график тригонометрической функции y=Sin x. Функция котангенс
18. Свойства и график тригонометрической функции y=tgx. Функция тангенс
19. Свойства и график тригонометрической функции y=cos x. Функция косинус
20. Простейшие тригонометрические уравнения cos x=a, ctg x=a.
21. Простейшие тригонометрические уравнения sin x=a, tg x=a.
Иррациональные уравнения. Уравнения, в которых поз знаком корня содержится переменная, называют иррациональными. Пример 1.
Ответ: 1,3. Пример 2.
Ответ: Пример 3. Решить уравнение Решение. Возведем обе части уравнения в квадрат. Произведем проверку полученных корней, для этого произведем подстановку значений переменной x в исходное уравнение. Пример 4. Решить уравнение Это уравнение можно решить по такой же методике как и в первом примере, но мы поступим иначе. Найдем ОДЗ данного уравнения. Из определения квадратного корня следует, что в данном уравнении одновременно должны выполнятся два условия: а) x - 9 x б) 1 - x -x x ОДЗ данного уранения: x Ответ: корней нет. Показательные уравнения. Логарифмы и их свойства. Логари́фм числа b по основанию a -определяется как показатель степени, в которую надо возвести основание a, чтобы получить число b. Обозначение: Основное логарифмическое тождество: При любом а>0 (а≠ 1) и любых положительных х и у выполнены равенства: 1. loga1=0.
2. logaa=1.
3. logaxy =logax + logay. Логарифм произведения равен сумме логарифмов.
4. loga
5. loga xp=p loga x для любого действительного р. Логарифм степени равен произведению показателя степени на логарифм основания этой степени. Функцию, заданную формулой y =logax, называют логарифмической функцией с основанием а. Логарифмические уравнения. Уравнение, содержащее неизвестное под знаком логарифма или (и) в его основании, называется логарифмическим уравнением. Простейшим логарифмическим уравнением является уравнение вида
Утверждение 1. Если a > 0, a ≠ 1, уравнение (1) при любом действительном b имеет единственное решение x = ab. Целые и рациональные числа. Действия с целыми и рациональными числами. Целые числа – это числа из множества {0, 1, -1, 2, -2,....}. Это множество состоит из трех частей – натуральные числа, отрицательные целые числа (противоположные натуральным числам) и число 0 (нуль). Целые числа обозначаются латинской буквой Z. Можно сказать, что Z ={1,2,3,....}. Рациональные числа – это числа, представимые в виде дроби Действительные числа. Действительные (вещественные) числа – это числа, которое применяются для измерения непрерывных величин. Множество действительных чисел обозначается латинской буквой R. Действительные числа включают в себя рациональные числа и иррациональные числа. Иррациональные числа – это числа, которые получаются в результате выполнения различных операций с рациональными числами (например, извлечение корня, вычисление логарифмов), но при этом не являются рациональными. Примеры иррациональных чисел – это
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 5396; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.216.248 (0.006 с.) |

 , где m — целое число, а n — натуральное число. Для обозначения рациональных чисел используется латинская буква Q. Все натуральные и целые числа – рациональные. Также в качестве примеров рациональных чисел можно привести:
, где m — целое число, а n — натуральное число. Для обозначения рациональных чисел используется латинская буква Q. Все натуральные и целые числа – рациональные. Также в качестве примеров рациональных чисел можно привести:  ,
,  ,
,  .
. ,
,  ,
, 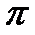 .
.



















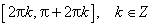

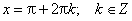

























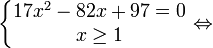



 - истинно:
- истинно: - истинно.
- истинно.  .
.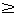 0;
0;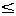 1.
1.
 .
. . Из определения следует, что записи
. Из определения следует, что записи  и
и  равносильны.
равносильны.
 =logax—logay. Логарифм частного равен разности логарифмов.
=logax—logay. Логарифм частного равен разности логарифмов.


