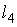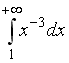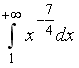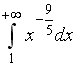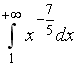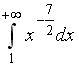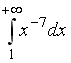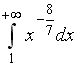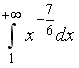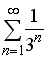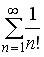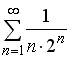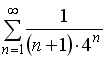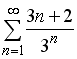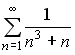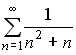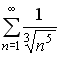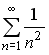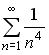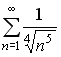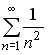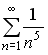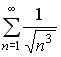Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
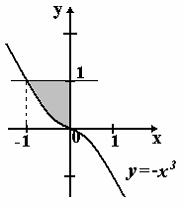
S: Площадь фигуры, изображенной на рисунке,Содержание книги
Поиск на нашем сайте
может быть вычислена как …
+:
S: Площадь фигуры, ограниченной линиями
+:
S: Площадь фигуры, ограниченной линиями +:
S: Показательная форма записи комплексного числа имеет вид: +:
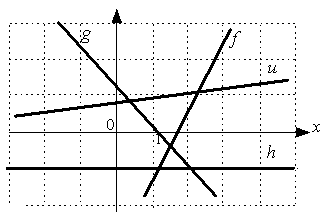
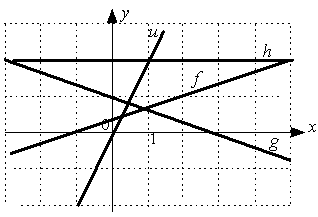
S: Положительный угловой коэффициент имеют прямые:
+: u +: f
S: Положительный угловой коэффициент имеют прямые:
+: u +: f
S: Полный дифференциал функции +: S: Полный дифференциал функции +: S: Полный дифференциал функции +: S: Полный дифференциал функции +:
S: Полный дифференциал функции +:
S: Полный дифференциал функции +:
S: Предел функции +: 1
S: Предел функции +: 5
S: Предел функции +: 5
S: Предел функции +: 2
S: Предел функции +: 1/2
S: Предел функции +: 3
S: Предел функции +: 2
S: Предел функции +: 4
S: Предел функции +: 2
S: Предел функции +: -1 S: Предел функции +: -2
S: Предел функции +: 3
S: Предел функции +: 0
S: Предел функции +: 0
S: Предел функции +: 0
S: Предел функции +: 0
S: Предел функции +: 0
S: Предел функции +: 0
S: Предел функции +: 0
S: Предел функции +: 0
S: Предел функции +: 0
S: Предел функции +: -2
S: Предел функции +: -1/4
S: Предел функции +: -3/2
S: Предел функции +: 3/10
S: Предел функции +: 5/14
S: Предел функции +: 7/4
S: Предел функции +: 7/10
S: Предел функции +: -5/4
S: Предел функции +: 2/5
S: Предел функции +: 1/6
S: Предел функции +: 3/8
S: Предел функции +: 7/12
S: Предел функции +: 5/14
S: Предел функции +: 7/12
S: Предел функции +: 5/12
S: Предел функции +: 3/8
S: Предел функции +:1/4
S: Предел функции +: 3/4
S: Предел функции +: 7/12
S: Предел функции +: 3/10
S: Предел функции +: 3/8
S: Предел функции +: 1/4
S: Предел функции +: 3/4
S: Предел функции +: -5/2
S: Предел функции +: 0
S: Предел функции +: бесконечность
S: Предел функции +: 10
S: Предел функции +: 14
S: Предел функции +: -10
S: Предел функции +: -14
S: Предел функции +: 12
S: Предел функции +: -12 S: Предел функции +: 6 S: Предел функции +: -6
S: Предел функции +: 3
S: Предел функции +: 3/4
S: Предел функции +: 0
S: Предел функции +: бесконечность
S: При решении системы линейных уравнений с квадратной матрицей коэффициентов +: столбцы матрицы S: При решении системы линейных уравнений с квадратной матрицей коэффициентов +: строки матрицы +: определитель матрицы
S: При решении системы линейных уравнений с квадратной матрицей коэффициентов +: строки матрицы +: определитель матрицы
S: При решении системы линейных уравнений с квадратной матрицей коэффициентов +: ни одна из строк матрицы +: ранг матрицы
S: При решении системы линейных уравнений с квадратной матрицей коэффициентов +: ранг матрицы +: одна из строк матрицы
S: Признак Даламбера сходимости числового ряда заключается в том, что … +:
S: Признак Коши сходимости числового ряда заключается в том, что … +:
S: Производная функции +:
S: Производная функции +:
S: Производная функции +:
S: Производная функции +:
S: Производная функции +:
S: Производная функции +: 2/3
S: Производная функции +: -1
S: Производная функции +: 0
S: Производная функции +: 1
S: Производная функции +: 0
S: Производная функции +: 2
S: Производная функции +: 0
S: Производная функции +: 1/2
S: Производная функции +: 0
S: Производная функции +: 1
S: Производная функции +: 0
S: Производная функции +: 1
S: Производная функции +: 3
S: Производная функции +: 2
S: Производная функции +: 0
S: Производная функции +: 8
S: Производная функции +: 15
S: Производная функции +: 4
S: Производная функции +: 6 S: Производная функции +: -12
S: Производная функции +: -15
S: Производная функции +: 9
S: Производная функции +: 8
S: Производная функции +: -9
S: Производная функции +: 4
S: Производная функции +: -3
S: Производная функции +: -4
S: Производная функции +: 1
S: Производная функции +: -9
S: Производная функции +: -10
S: Производная функции +:
S: Производная функции +:
S: Производная функции +:
S: Производная функции +:
S: Производная функции +: S: Производная функции +:
S: Производная функции +:
S: Производная второго порядка функции -: -: -: -:
S: Производная второго порядка функции +: -1
S: Производная второго порядка функции +: 0
S: Производная второго порядка функции +: 12
S: Производная второго порядка функции +: 18
S: Производная второго порядка функции +: 0
S: Производная второго порядка функции +: 47
S: Производная второго порядка функции +: 14
S: Производная второго порядка функции +: 78
S: Производная второго порядка функции +: 15
S: Производная второго порядка функции +: 198
S: Прямая +: 3
S: Прямая +:
S: Прямые +: 6
S: Прямые +: 6
S: Прямые +: -2
S: Прямые +: -1/2
S: Прямые +: -2
S: Прямая проходит через точки +:
S: Радиус сходимости степенного ряда +: 1
S: Радиус сходимости ряда +:
S: Радиус сходимости степенного ряда +: (–8;8)
S: Радиус сходимости степенного ряда +: (–7;7) S: Радиус сходимости степенного ряда +: (–3;3)
S: Радиус сходимости степенного ряда +: (–14;14)
S: Радиус сходимости степенного ряда +: (–16;16)
S: Разложение функции +:
S: Ранг матрицы +: 2
S: Ранг матрицы +: 1 S: Ранг матрицы +: 1
S: Ранг матрицы +: 4
S: Ранг матрицы +: 3
S: Ранг матрицы +: 4
S: Ранг матрицы +: – 9
S: Ранг матрицы +: 2
S: Ранг матрицы +: 3 S: Расстояние от точки +:
S: Расстояние от точки +: 7
S: Расстояние между фокусами эллипса +: 6
S: Расстояние между фокусами эллипса +: 16
S Расстояние между фокусами гиперболы +: 26
S: Расстояние между фокусами гиперболы +: 40
S: Расстояние между фокусами гиперболы +: 50 S: Ряд +: ряд
S: С помощью преобразования параллельного переноса осей координат уравнение кривой +:
S: Система линейных уравнений +: – 4
S: Система линейных уравнений +: – 2
S: Система линейных уравнений +: -2
S: Система линейных уравнений +: -6
S: Система линейных уравнений L1: L2: L3: R1: 6 R2: 14 R3: – 4
S: Система линейных уравнений L1: L2: L3: R1: 23 R2: 11 R3: 5
S: Система линейных уравнений L1: L2: L3: R1: 16 R2: 2 R3: 3
S: Система линейных уравнений L1: L2: L3: R1: 27 R2: 13 R3: – 3
S: Система линейных уравнений L1: L2: L3: R1: – 1 R2: 7 R3: 6
S: Смешанная производная второго порядка функции +: –3
S: Смешанная производная второго порядка функции
+: 3
S: Смешанная производная второго порядка функции +: -3
S: Смешанная производная второго порядка функции +:
S: Смешанная производная второго порядка функции +:
S: Смешанная производная второго порядка функции +:
S: Соотношение +: окружность
S: Среди перечисленных уравнений дифференциальными уравнениями первого порядка являются … +: +:
S: Среди перечисленных уравнений дифференциальными уравнениями второго порядка являются … +: +:
S: Среди перечисленных уравнений дифференциальными уравнениями второго порядка являются … +: +:
S: Среди перечисленных уравнений дифференциальными уравнениями первого порядка являются … +: +:
S: Среди перечисленных уравнений дифференциальными уравнениями первого порядка являются … +: +:
S: Среди перечисленных уравнений дифференциальными уравнениями первого порядка являются … +: +:
S: Среди перечисленных уравнений дифференциальными уравнениями первого порядка являются … +: +: S: Среди перечисленных уравнений дифференциальными уравнениями первого порядка являются … +: +:
S: Среди перечисленных уравнений дифференциальными уравнениями первого порядка являются … +: +:
S: Среди перечисленных уравнений дифференциальными уравнениями первого порядка являются … +: +:
S: Среди прямых +: +:
S: Сходящимися являются несобственные интегралы … +: +:
S: Сходящимися являются несобственные интегралы … +: +:
S: Сходящимися являются несобственные интегралы … +: +:
S: Сходящимися являются несобственные интегралы … +: +:
S: Сходящимися являются несобственные интегралы … +: +:
S: Сходящимися среди приведенных ниже числовых рядов являются … +: +:
S: Сходящимися среди приведенных ниже числовых рядов являются … +: +:
S: Сходящимися среди приведенных ниже числовых рядов являются … +: +:
S: Сходящимися среди приведенных ниже числовых рядов являются … +: +:
S: Сходящимися среди приведенных ниже числовых рядов являются … +: +:
S: Сходящимися среди приведенных ниже числовых рядов являются … +: +:
S: Сходящимися среди приведенных ниже числовых рядов являются … +: +:
S: Сходящимися среди приведенных ниже числовых рядов являются … +: +:
S: Сходящимися среди приведенных ниже числовых рядов являются … +: +:
S: Сходящимися среди приведенных ниже числовых рядов являются … +: | ||
|
| Поделиться: |

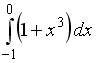
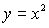 ,
, 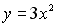 ,
,  , вычисляется с помощью определенного интеграла…
, вычисляется с помощью определенного интеграла…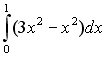
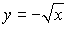 ,
, 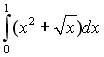
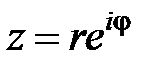
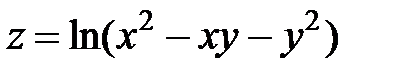 равен …
равен …
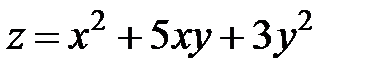 равен …
равен …
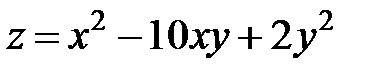 равен …
равен …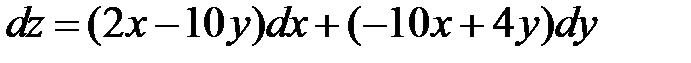
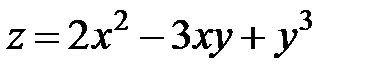 в точке
в точке  равен …
равен …
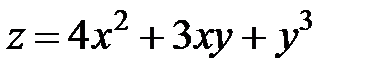 в точке
в точке  равен …
равен …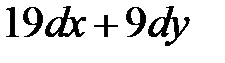
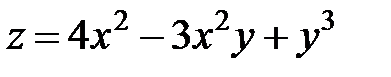 в точке
в точке  равен …
равен …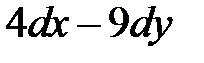
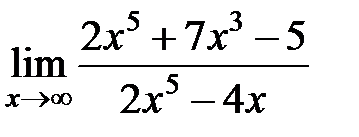 равен...
равен...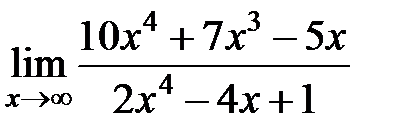 равен...
равен...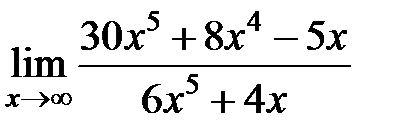 равен...
равен...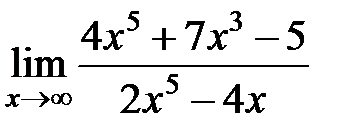 равен...
равен...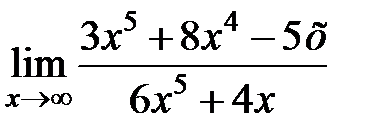 равен...
равен...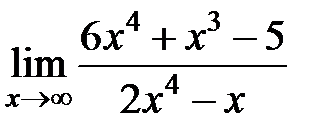 равен...
равен... равен...
равен...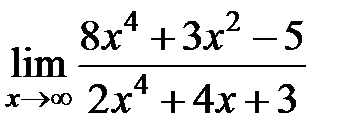 равен...
равен... равен...
равен... равен...
равен...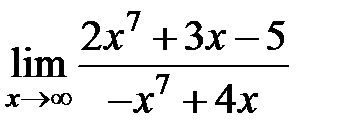 равен...
равен... равен...
равен...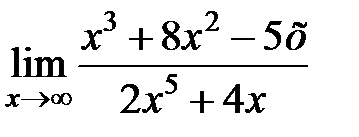 равен...
равен...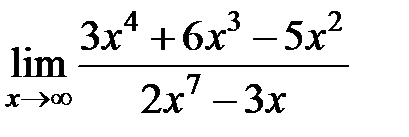 равен...
равен...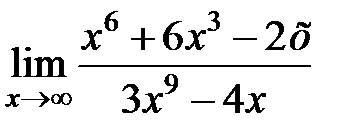 равен...
равен...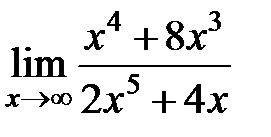 равен...
равен...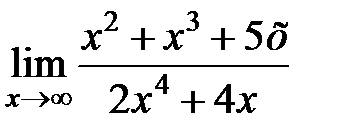 равен...
равен... равен
равен равен...
равен...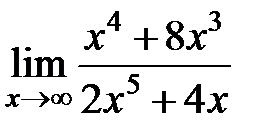 равен...
равен... равен...
равен...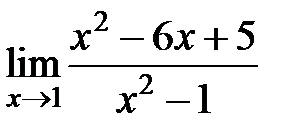 равен...
равен... равен...
равен...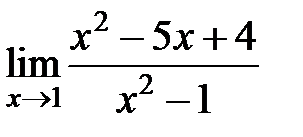 равен...
равен...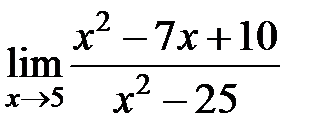 равен...
равен... равен...
равен...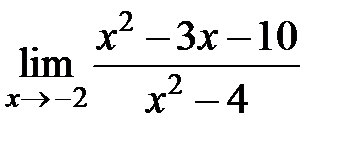 равен...
равен... равен...
равен...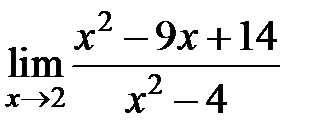 равен...
равен...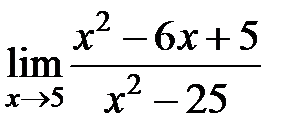 равен...
равен...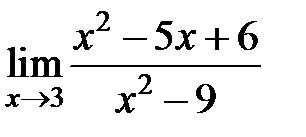 равен...
равен...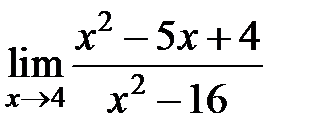 равен...
равен... равен...
равен...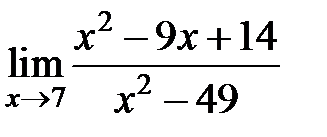 равен...
равен...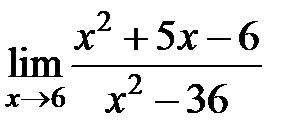 равен...
равен...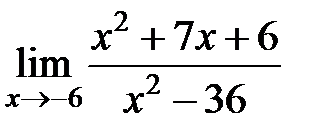 равен...
равен... равен...
равен... равен...
равен... равен...
равен... равен...
равен... равен...
равен...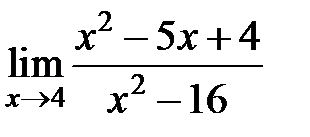 равен...
равен...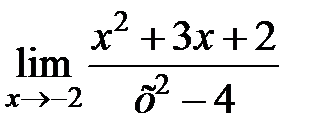 равен...
равен...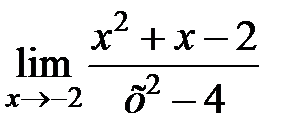 равен...
равен...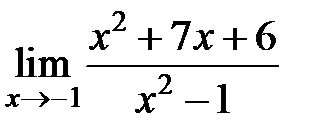 равен...
равен...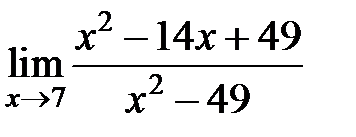 равен...
равен...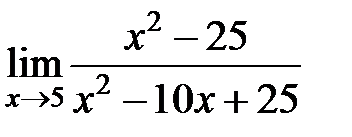 равен...
равен... равен...
равен...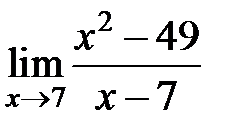 равен...
равен...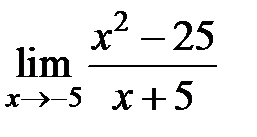 равен...
равен...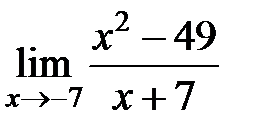 равен...
равен...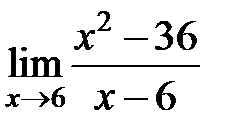 равен...
равен...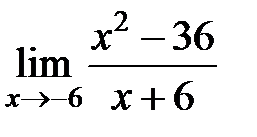 равен...
равен...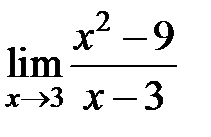 равен...
равен... равен...
равен...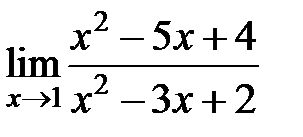 равен...
равен...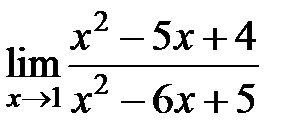 равен...
равен...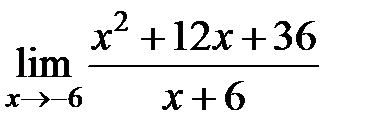 равен...
равен...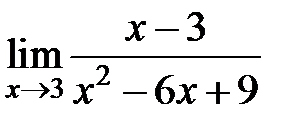 равен...
равен...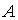 можно применять формулы Крамера, если
можно применять формулы Крамера, если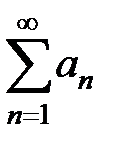 с положительными членами
с положительными членами 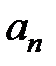
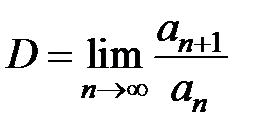 , при
, при  - ряд сходится, при
- ряд сходится, при 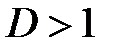 - ряд расходится
- ряд расходится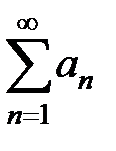 с положительными членами
с положительными членами 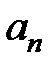
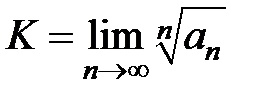 , при
, при 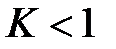 - ряд сходится, при
- ряд сходится, при 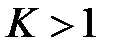 - ряд расходится
- ряд расходится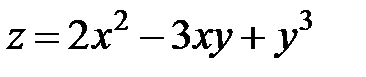 по направлению вектора
по направлению вектора 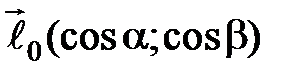 в точке
в точке 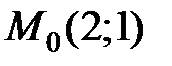 имеет вид …
имеет вид …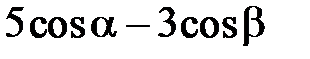
 по направлению вектора
по направлению вектора 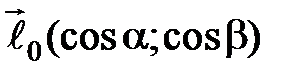 в точке
в точке  имеет вид …
имеет вид …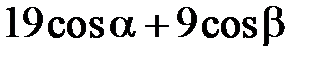
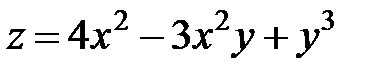 по направлению вектора
по направлению вектора 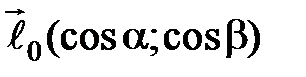 в точке
в точке 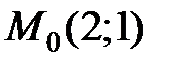 имеет вид …
имеет вид …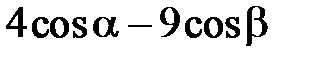
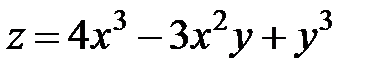 по направлению вектора
по направлению вектора 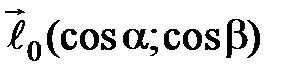 в точке
в точке  имеет вид …
имеет вид …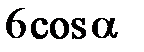
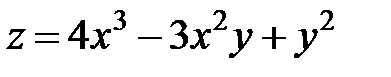 по направлению вектора
по направлению вектора 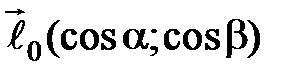 в точке
в точке 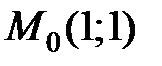 имеет вид …
имеет вид …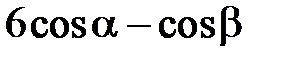
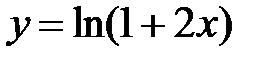 в точке
в точке  равна...
равна...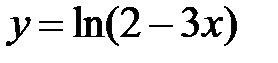 в точке
в точке 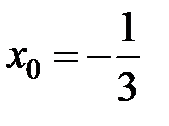 равна...
равна... в точке
в точке 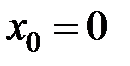 равна...
равна...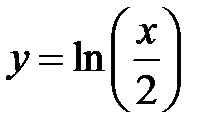 в точке
в точке 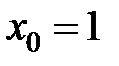 равна...
равна...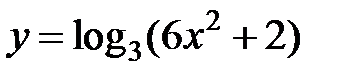 в точке
в точке 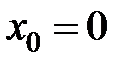 равна...
равна...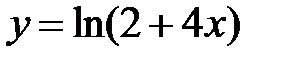 в точке
в точке  равна...
равна...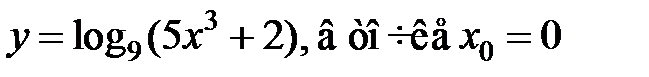 равна...
равна... в точке
в точке 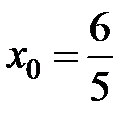 равна...
равна... в точке
в точке 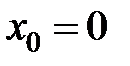 равна...
равна...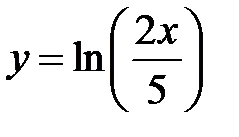 в точке
в точке 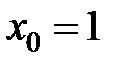 равна...
равна... в точке
в точке 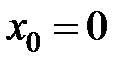 равна...
равна... в точке
в точке  равна...
равна...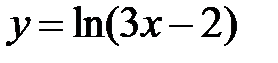 в точке
в точке 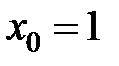 равна...
равна...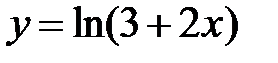 в точке
в точке  равна...
равна...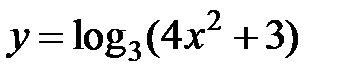 в точке
в точке 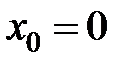 равна...
равна... в точке
в точке 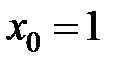
 в точке
в точке  равна...
равна...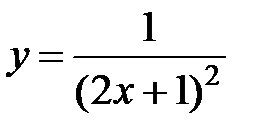 в точке
в точке 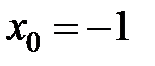 равна...
равна...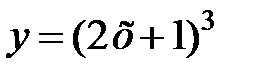 в точке
в точке  равна...
равна...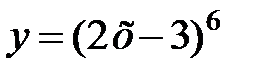 в точке
в точке 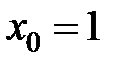 равна...
равна...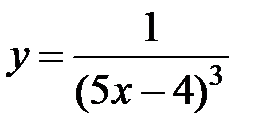 в точке
в точке 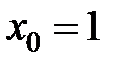 равна...
равна...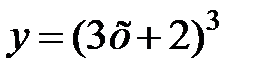 в точке
в точке 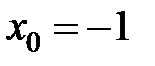 равна...
равна...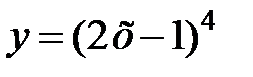 в точке
в точке  равна...
равна... в точке
в точке 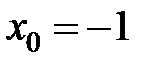 равна...
равна...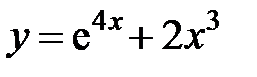 в точке
в точке 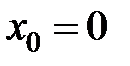 равна...
равна...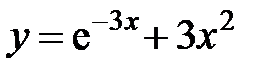 в точке
в точке 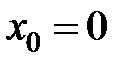 равна...
равна... в точке
в точке 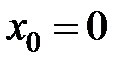 равна...
равна...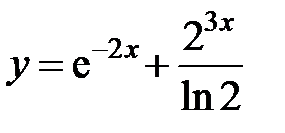 в точке
в точке 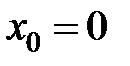 равна...
равна...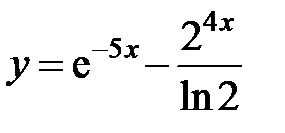 в точке
в точке 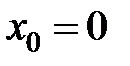 равна...
равна...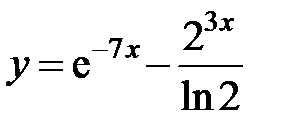
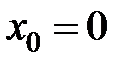 равна...
равна... равна …
равна …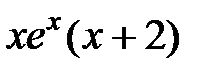
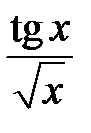 равна…
равна…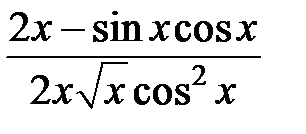
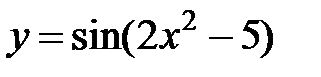 равна…
равна…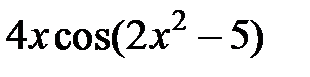
 равна…
равна…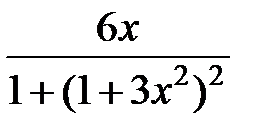
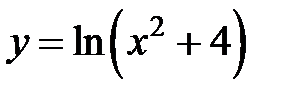 равна…
равна…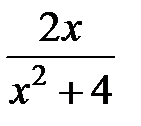
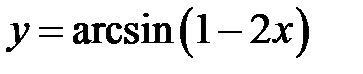 равна…
равна…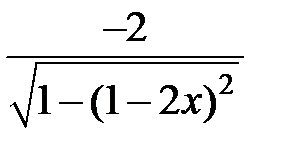
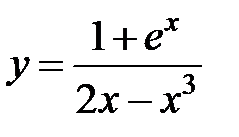 равна…
равна…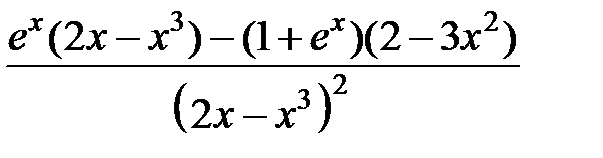
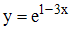 равна …
равна …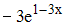
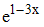
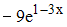
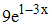
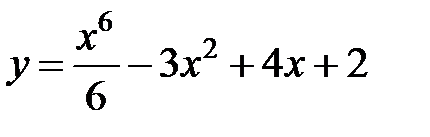 в точке
в точке 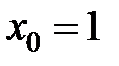 равна...
равна...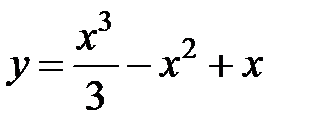 в точке
в точке 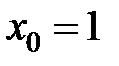 равна...
равна... в точке
в точке 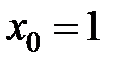 равна...
равна... в точке
в точке 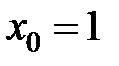 равна...
равна... в точке
в точке 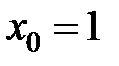 равна...
равна... в точке
в точке 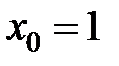 равна...
равна...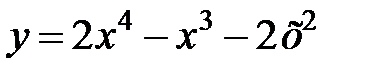 в точке
в точке 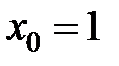 равна...
равна...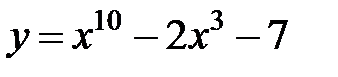 в точке
в точке 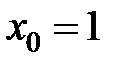 равна...
равна...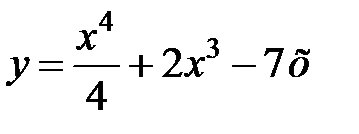 в точке
в точке  равна...
равна...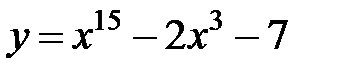 в точке
в точке 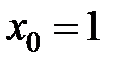 равна...
равна...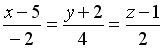 пересекает плоскость
пересекает плоскость 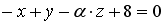 в том случае, когда
в том случае, когда 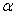 не равно …
не равно …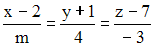 и плоскость
и плоскость 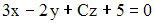 перпендикулярны при значениях m и С, равных …
перпендикулярны при значениях m и С, равных …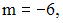
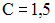
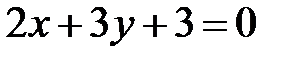 и
и 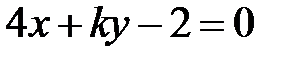 параллельны при
параллельны при 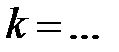
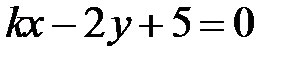 и
и 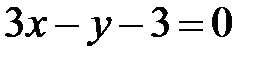 параллельны при
параллельны при 
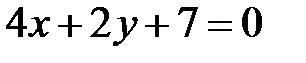 и
и  параллельны при
параллельны при 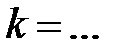
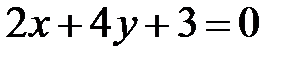 и
и 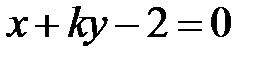 перпендикулярны при
перпендикулярны при 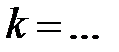
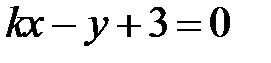 и
и 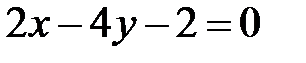 перпендикулярны при
перпендикулярны при 
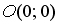 и
и 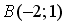 . Тогда ее угловой коэффициент равен…
. Тогда ее угловой коэффициент равен…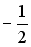
 равен …
равен …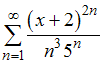 равен …
равен …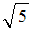
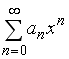 равен 8, тогда интервал сходимости имеет вид…
равен 8, тогда интервал сходимости имеет вид…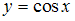 в ряд по степеням
в ряд по степеням 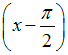 имеет вид …
имеет вид …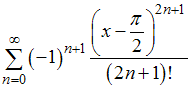
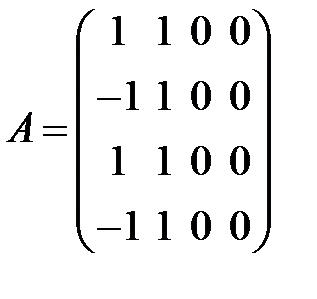 равен …
равен … равен …
равен …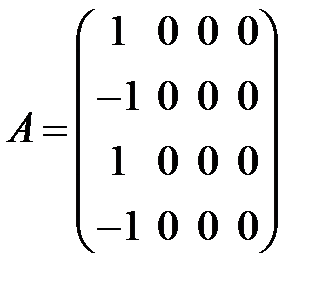 равен …
равен …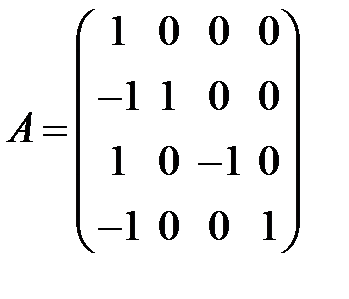 равен …
равен …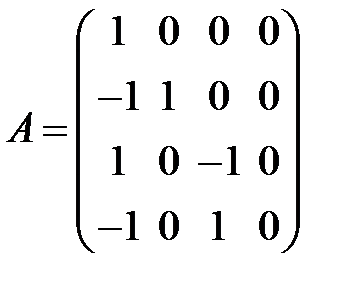 равен …
равен … равен …
равен …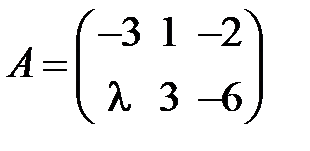 равен рангу матрицы
равен рангу матрицы 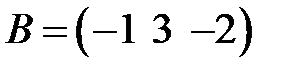 при
при 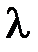 , равном …
, равном …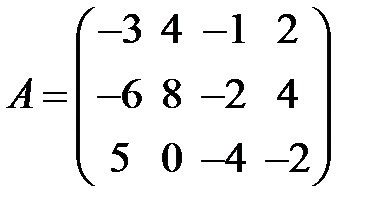 равен …
равен …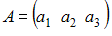 , где
, где 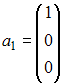 ,
, 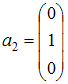 ,
, 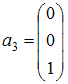 , равен …
, равен …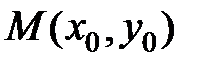 до прямой
до прямой  можно найти по формуле
можно найти по формуле
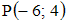 до прямой
до прямой 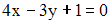 равно …
равно …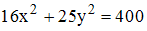 равно …
равно …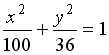 равно …
равно … равно …
равно …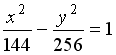 равно …
равно …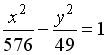 равно …
равно …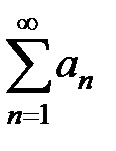 называется абсолютно сходящимся, если
называется абсолютно сходящимся, если сходится
сходится приводится к каноническому виду…
приводится к каноническому виду…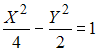
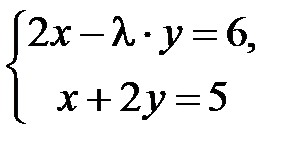 не имеет решений, если
не имеет решений, если 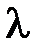 равно …
равно …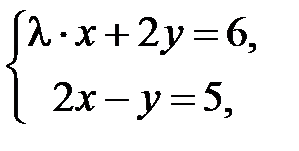 не имеет решений, если
не имеет решений, если 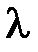 равно …
равно …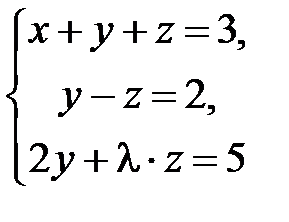 не имеет решений, если
не имеет решений, если 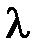 равно …
равно …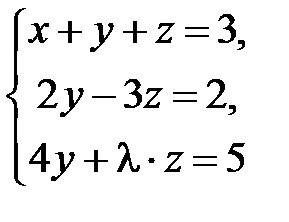 не имеет решений, если
не имеет решений, если  равно …
равно …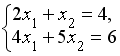 решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
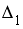
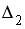
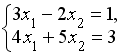 решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.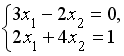 решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.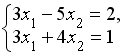 решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.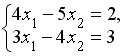 решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.
решается по правилу Крамера. Установите соответствие между определителями системы и их значениями.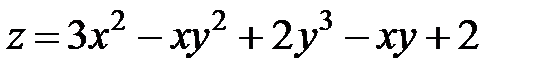 в точке
в точке 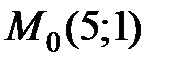 равна …
равна … в точке
в точке 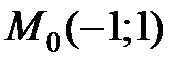 равна …
равна …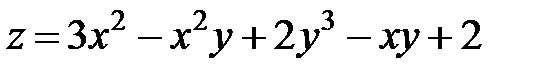 в точке
в точке 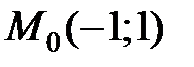 равна …
равна …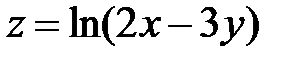 равна …
равна …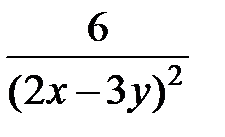
 равна …
равна …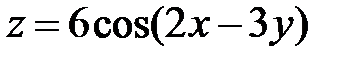
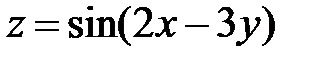 равна …
равна …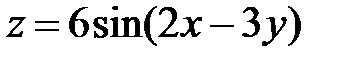
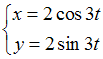 на плоскости
на плоскости 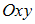 задает …
задает …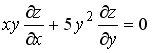
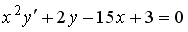
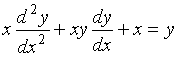
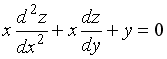
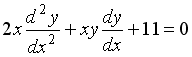

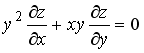
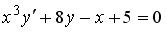
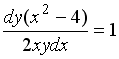
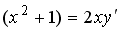
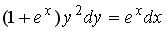
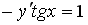
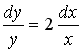
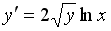
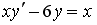
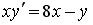
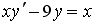
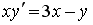

 ,
, 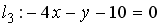 ,
,  параллельными являются …
параллельными являются … и
и 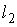
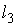 и
и