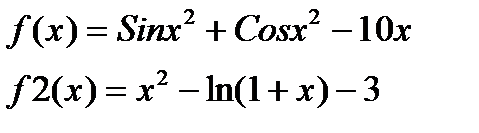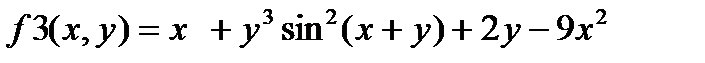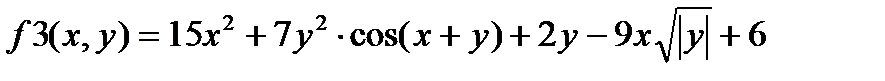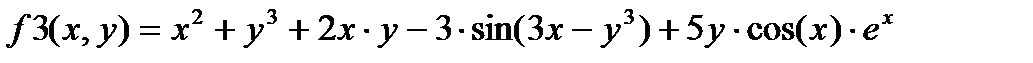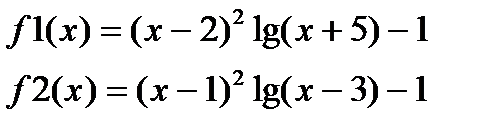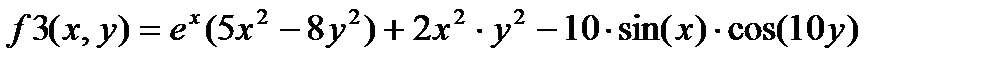Построение графиков и визуализация вычислений в системе MatLab

 

Самый простой способ для построения графика функции одной переменной y=f(x) - это предварительное формирование двух векторов одинаковой длины: век­тора значений аргументов x и вектора соответствующих им значений функции у, а затем выполнение команды plot(x, y). Выполнение команды plot(x, y) открывает графическое окно и отображает в нем график функции y(x).

Рассмотрим пример построения графика функции на отрезке [-1.5;1.5] (рис. 1.2.2-1).

 

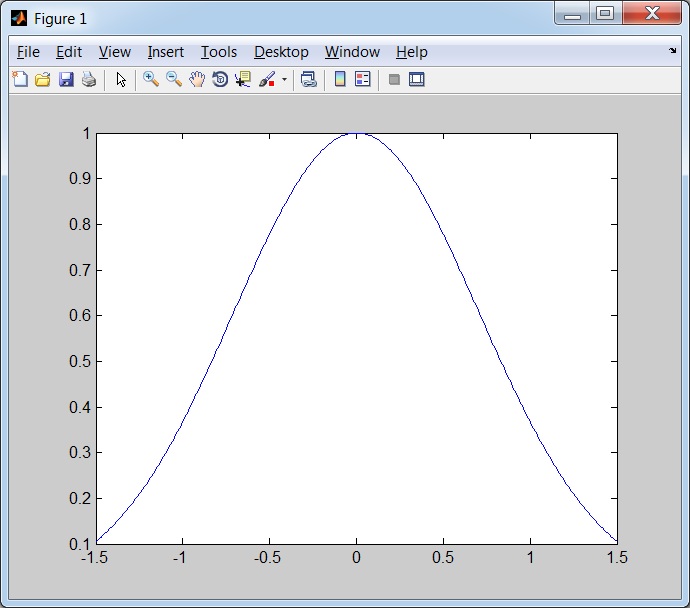
Рис. 1.2.2-1. Команды построения графика функции

В результате выполнения команды plot(x,y) появляется графическое окно с именем Figure 1 (рис. 1.2.2-2).

Рис. 1.2.2-2. Графическое окно с изображением графика функции

 

Переход между окнами (от командного окна к графическому окну и обратно) осуществляется с помощью комбинации клавиш < Alt+Tab> или с помощью мыши.

В общем случае, число аргументов у функции plot() не ограничивается двумя. Эта функция имеет следующий формат:

plot(x1,y1,x2,y2,...).

Таким образом, в одном графическом окне можно построить не один, а несколько графиков. Рассмотрим два способа построения в одном графическом окне трех графиков (рис. 1.2.2-3 и рис. 1.2.2-4).

 

Рис. 1.2.2-3. Использование векторов значений функций

для построения графиков трех функций

 

Рис. 1.2.2-4. Использование матрицы значений функций

для построения графиков трех функций

Приведенные в первом и втором примерах наборы команд позволяют получить один и тот же результат (рис. 1.2.2-5.) Разница в том, что в первом примере формируются три вектора значений функций (y1, y2, y3), а во втором – матрица y, содержащая значения функций в виде столбцов.

График, выведенный в графическое окно Matlab, может быть снабжен заголовком, именами осей, дополнительным текстом, сеткой и другой поясняющей информацией. Аргументами команд, управляющими пояснениями, являются текстовые строки. Например, команда title() добавит к графику заголовок. Команда grid on позволяет отобразить координатную сетку. Для вывода подписи осей используются команды Xlabel(), Ylabel().

 

 

Рис. 1.2.2-5. Графики функций y 1=sin(x); y2=sin(2*x); y3=sin(4*x)

 

Если в одном графическом окне создаются несколько графиков, полезно с использованием функции legend() отобразить легенду графиков. Ее текстовые аргументы соответствуют подписям соответствующих созданию кривых, а числовой параметр определяет место расположения в графическом окне (табл. 1.2.2-1).

Таблица 1.2.2-1

Значение аргумента	Размещение легенды
-1	В правом верхнем углу над областью графика
	Место выбирается автоматически, чтобы не перекрывать область кривых
	В правом верхнем углу (и по умолчанию)
	В левом верхнем углу области графика
	В левом нижнем углу области графика
	В правом нижнем углу области графика

 

При выводе в одно графическое окно нескольких графиков удобнее каждый график выводить с использованием своей команды plot(), однако в этом случае происходит создание нового графического окна. Для того чтобы этого избежать, используется команда holdon. Эта команда позволяет расположить все в дальнейшем выводимые графики в одном окне.

При выводе графика можно сменить принятый по умолчанию Matlab цвет и тип точек, с помощью которых рисуется данный график (табл.1.2.2-2). Символы, указывающие на цвет и тип точки, заключаются в апострофы и указываются в команде plot() после имени функции.

Таблица 1.2.2-2

Символ	Цвет	Символ	Маркер
y	желтый	.	точка
m	фиолетовый	кружок	:
c	голубой	x	x-метка
r	красный	+	плюс
g	зеленый	*	звездочка
b	синий	s	квадрат
w	белый	d	алмаз
k	черный	v	треугольник(вниз)
?	треугольник (вверх)	-	сплошная
<	треугольник (влево)		точечная
>	треугольник (вправо)	-.	штрих - пунктирная
p	шестиугольник	-	пунктирная
h	восьмиугольник

 

Рассмотрим пример (рис. 1.2.2-6), в котором используются перечисленные выше опции, инструкции и функции. Результат выполнения инструкций, комментирующих графики, приведен на рис. 1.2.2-7.

Рис. 1.2.2-6. Использование инструкций при построении графиков

 

Рис. 1.2.2-7. Результат выполнения инструкций,

комментирующих графики

 

Большую часть вышеописанных действий можно реализовать также с помощью команд инструментальной панели графических окон (рис. 1.2.1-8).

 

 

Рис. 1.2.2-8. Компоненты меню графического окна

 

Команды основного меню графического окна представляют большой набор средств, предназначенных для отображения и оформления графиков, позволяющих в интерактивном режиме и без использования команд придать графику желаемый вид, а кнопки панели дублируют наиболее часто используемые пункты меню, ускоряя тем самым доступ к ним.

 

Трехмерные поверхности обычно описываются функцией двух переменных z(x,у). Для построения трехмерных графиков необходимо сформировать два двумерных массива, например, X и Y с использованием функции meshgrid() ( рис. 1.2.2-9).

 

 

Рис. 1.2.2-9. Формирование двумерных массивов функцией meshgrid()

 

Рис. 1.2.2-10. Построение различных видов графиков

функций двух переменных

 

Сформированные в виде двумерных массивов данные используются функциями:

 

· mesh(X,Y,Z) – построение сетчатого графика;

· contour(X,Y,Z) – построение графика контурных линий;

· surf(X,Y,Z) – построения графика сплошной поверхности;

· surfс(X,Y,Z) – построения графика сплошной поверхности и контурных линий;

· plot3(X,Y,Z) – построение точек, соединенных отрезками прямых и др.

 

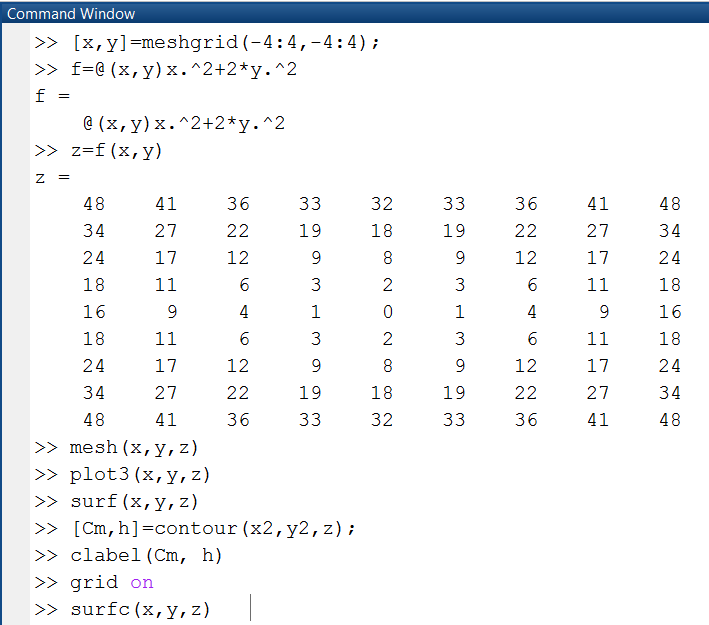
Рассмотрим примеры использования перечисленных выше функций, для чего сформируем матрицу z(x,y) с использованием функции f(x,y)
(рис. 1.2.2-10).

Результатом выполнения команды mesh(x,y,z) является построение графика поверхности в виде сетки (рис. 1.2.2-11).

 

 

Рис. 1.2.2-11. Результат выполнения команды mesh(x,y,z)

 

В результате выполнения команды plot3(x,y,z) происходит построение графика поверхности, где точка соединены отрезками прямой
(рис. 1.2.2-12).

 

 

Рис. 1.2.2-12. Результат выполнения команды plot3(x,y,z)

 

Команда surf(x,y,z) выполняет построение графика сплошной поверхности (рис. 1.2.2-13).

 

 

Рис. 1.2.2-13. Результат выполнения команды surf(x,y,z)

 

Команда contour(x,y,z) позволяет получить график контурных линий (рис. 1.2.2-14).

 

 

Рис. 1.2.2-14. Результат выполнения команды contour(x,y,z)

 

 

Рис. 1.2.2-15

 

Добавление команд, представленных на рис. 1.2.2-15, позволяет нанести на контурные линии значения функции в отдельных точках
(рис. 1.2.2-16).

 

Рис. 1.2.2-16. График контурных линий с

нанесенными значениями функции

Команда surfс(x,y,z) предназначена для построения графика сплошной поверхности, дополненного контурными линиями (рис. 1.2.2-17).

 

 

Рис. 1.2.2-17. Результат выполнения команды surfс(x,y,z)

 

 

Лабораторная работа по теме

«Векторы, матрицы и построение графиков

В системе Matlab»

 

 

Вопросы, подлежащие изучению

1) Работа с векторами и матрицами.

2) Построение графиков функций одной переменной.

3) Средства инструментальной панели графических окон.

4) Построение трехмерных изображений с использованием функций Matlab mesh(), plot3(), surf(), surfс() и controur().

 

 

2. Общее задание

 

1) Изучите материал Темы 1.2 (п.п. 1.2.1 – 1.2.2).

2) Выберите вариант индивидуального задания из табл. 1.3.3-1.

3) Выполните команду clear all для очистки Рабочей области.

4) Опишите функцию f1(x) и получите ее символьное выражение.

5) Задайте диапазон изменения аргумента функции f1(x) и вычислите ее значения.

6) Задайте диапазон изменения аргумента функции f1(x) для построения графика.

7) Выполните команду plot() для получения графика f1(x).

8) Опишите функцию f2(x).

9) Разместите графики функций f1(x) и f2(x) в одном окне, для чего после построения графика первой функции выполните команду hold on.

10) Дополните графики необходимыми пояснениями: заголовок, имена осей, координатная сетка и легенда.

11) Задайте диапазоны изменения значений x и y для функций f3(x,y) и получите таблицы их значений.

12) Опишите функцию f3(x, y).

13) Получите таблицу значений функции f3(x,y).

14) Получите график функции f3(x, y) с использованием команд mesh(), plot3(), surf(), surfс() и controur().

15) Сохраните текст рабочего окна на внешнем носителе.

16) Представьте результаты работы преподавателю, ответьте на поставленные вопросы.

17) Выполните команду clear all для очистки Рабочей среды.

18) Оформите отчет по выполненной работе.

 

Варианты индивидуальных заданий

 

Таблица 1.3.3-1

 

 

Содержание отчета

 

1) В форме комментариев:

· Название лабораторной работы

· ФИО студента, номер группы

· № варианта

· Индивидуальное задание

2) Протокол вычислений (сессии) в окне Command Window, снабженный соответствующими комментариями.

1.2.4. Контрольные вопросы по теме

1) Как создать вектор-строку?

2) Как создать вектор-столбец?

3) Как транспонировать векторы?

4) Какая функция служит для определения длины вектора?

5) Каким образом создать вектор с постоянным шагом?

6) Требуется ли при работе с векторами и матрицами предварительное объявление их размера?

7) Какой символ используется для разделения элементов матрицы в строке, а какой для разделения ее строк?

8) Какие команды предназначены для заполнения матрицы случайными числами, распределенными по равномерному или нормальному закону распределения?

9) Формат команд выбора минимального и максимального значения элемента матрицы.

10) Назначение команды plot().

11) Каким образом построить в одном графическом окне несколько графиков?

12) Какой пояснительной информацией может быть снабжен график, построенный в графическом окне?

13) Для чего используется функция legend()?

14) Каково назначение функции meshgrid() при построении трехмерных изображений?

15) Какие типы графиков позволяют строить встроенные функции: contour(), surf(), survc() и plot3()?