
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование функций и построение их графиковСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Исследование функций и построение их графиков удобно выпол-нять по следующей схеме. 1. Найти область определения функции. 2. Выяснить, является ли функция четной, нечетной, периодической. 3. Исследовать функцию на непрерывность, найти точки разрыва. 4. Найти асимптоты графика функции. 5. Установить интервалы монотонности функции. Найти точки экстремума функции, вычислить значения функции в этих точках. 6. Определить интервалы выпуклости и вогнутости графика функции, точки перегиба. 7. Используя результаты проведенного исследования, построить график функции. При необходимости уточнения отдельных участков кривой можно вычислить координаты нескольких дополнительных точек (в частности, координаты точек пересечения графика с осями координат).
Пример 7.4. Исследовать функцию Функция определена и непрерывна на всей оси, кроме точек Функция нечетная, так как
Следовательно, Производная функции Вторая производная
обращается в нуль при Составим таблицу
Следовательно, Используя полученные данные, строим график функции (рис. 7.1).
Рис. 7.1
КОНТРОЛЬНАЯ РАБОТА № 1
1 – 20. Решить системы по формулам Крамера, матричным способом и методом Гаусса.
1.
3. 5.
7.
9.
11.
13.
15.
17.
19.
21 – 40. Даны вершины треугольника А, В, С. Найти уравнение и длину высоты, опущенной из вершины В.
21.
23.
25.
27.
29.
31.
33.
35.
37.
39.
41 – 60. Найти угол (в градусах) между плоскостью
41.
42.
43. 44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60. 61 – 80. Упростить уравнение кривой и изобразить ее на рисунке.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80. 81 – 100. Найти пределы функций, не пользуясь правилом Лопиталя.
81. а) в) 82. а) в) 83. а) в) 84. а) в) 85. а) в) 86. а) в) 87. а) в) 88. а) в) 89. а) в) 90. а) в) 91. а) в) 92. а) в) 93. а) в) 94. а) в) 95. а) в) 96. а) в) 97. а) в) 98. а) в) 99. а) в) 100. а) в)
101 – 120. Исследовать данные функции на непрерывность и указать вид точек разрыва; в условии б дополнительно построить график функции.
101. а)
102. а)
103. а)
104. а) 105. а)
106. а)
107. а)
108. а)
109. а)
110. а)
111. а) 112. а)
113. а)
114. а)
115. а)
116. а)
117. а)
118. а) 119. а) 120. а)
121 – 140. Найти производные первого и второго порядков от функ-ций, заданных параметрически:
121.
122.
123.
124.
125.
126.
127.
128.
129.
130.
131.
132.
133. 134.
135.
136.
137.
138.
139.
140.
141 – 160. Написать формулу Тейлора третьего порядка с остаточным членом в форме Лагранжа для заданной функции в точке
141. 143.
145.
147.
149.
151.
153.
155.
157.
159.
161-180. Исследовать функцию и построить ее график.
161.
164.
167.
170.
173.
176.
179.
Литература 1. Математика: сборник заданий для аудиторной и самостоятельной работы студентов инженерно-технических специальностей втузов: в 2 ч. / А.Н. Андриянчик [и др.]: – Минск: БНТУ, 2005. – Ч. 1. 2. Элементы линейной алгебры и аналитической геометрии / Р.Ф. Апатенок [и др.]. – Минск: Вышэйшая школа, 1986.
3. Гусак, А.А. Высшая математика: в 2 т. / А.А. Гусак. – Минск: Изд-во БГУ, 1978, 1983. – Т. 1, 2. 4. Данко, П.Е. Высшая математика в упражнениях и задачах: 5. Жевняк, Р.М. Высшая математика: в 2 ч. / Р.М. Жевняк, А.А. Карпук. – Минск: Вышэйшая школа, 1984, 1985. – Ч. 1, 2. 6. Клетеник, Д.В. Сборник задач по аналитической геометрии / Д.В. Клетеник. – М.: Наука, 1986. 7. Кудрявцев, Л.Д. Краткий курс математического анализа / Л.Д. Кудрявцев. – М.: Наука, 1989. 8. Пискунов, Н.С. Дифференциальное и интегральное исчисление для втузов: в 3 т. / Н.С. Пискунов. – М.: Наука, 1985. – Т. 1–3. 9. Сухая, Т.А. Задачи по высшей математике: учебное пособие: в 2 ч. / Т.А. Сухая. – Минск: Вышэйшая школа, 1993. 10. Высшая математика для инженеров / С.А. Минюк [и др.] / под ред. Н.А. Микулика. – Минск: Элайда, 2007. – Т. 1, 2. 11. Индивидуальные задания по высшей математике: в 4 ч. / под ред. А.П. Рябушко. – Минск: Вышэйшая школа, 2004.
С о д е р ж а н и е
Учебное издание
ВЫСШАЯ МАТЕМАТИКА
Методические указания и контрольная работа № 1 для студентов-заочников машиностроительных специальностей
Составители: АНДРИЯНЧИК Анатолий Николаевич МИКУЛИК Николай Александрович ЮРИНОК Виктор Иванович
Редактор Т.Н. Микулик Компьютерная верстка Н.А. Школьниковой Подписано в печать 19.02.2010. Формат 60´84 1/16. Бумага офсетная. Отпечатано на ризографе. Гарнитура Таймс. Усл. печ. л. 4,65. Уч.-изд. л. 3,64. Тираж 700. Заказ 145. Издатель и полиграфическое исполнение: Белорусский национальный технический университет. ЛИ 02330/0494349 от 16.03.2009. Проспект Независимости, 65. 220013, Минск.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 481; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.165.168 (0.009 с.) |

 и построить ее график.
и построить ее график.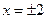 .
. , ее график симметричен относительно начала координат, поэтому достаточно исследовать функцию для
, ее график симметричен относительно начала координат, поэтому достаточно исследовать функцию для 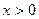 . Прямые х = –2 и х = 2 являются вертикальными асимптотами, поскольку
. Прямые х = –2 и х = 2 являются вертикальными асимптотами, поскольку  . Найдем наклонные асимптоты
. Найдем наклонные асимптоты 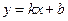 :
: ;
;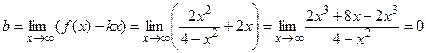 .
. – наклонная асимптота.
– наклонная асимптота. обращается в нуль при
обращается в нуль при  и
и 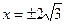 .
.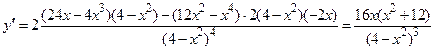
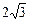 )
)
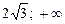 )
)
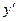
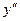

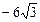
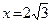 – точка максимума,
– точка максимума,  . В силу нечетности имеем:
. В силу нечетности имеем:  – точка минимума
– точка минимума  . Поскольку
. Поскольку 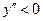 при
при  и
и 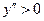 при
при 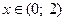 , то х = 0 – абсцисса точки перегиба, 0(0;0) – точка перегиба.
, то х = 0 – абсцисса точки перегиба, 0(0;0) – точка перегиба.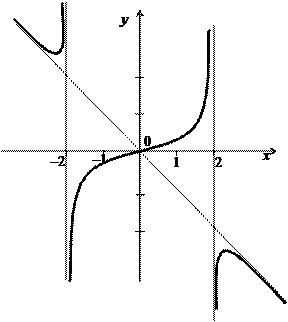
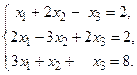 2.
2. 
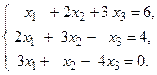 4.
4. 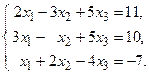
 6.
6. 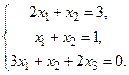
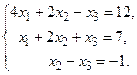 8.
8. 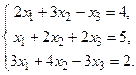
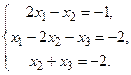 10.
10. 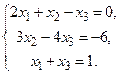
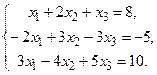 12.
12. 
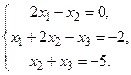 14.
14. 
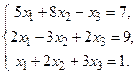 16.
16. 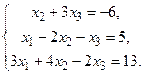
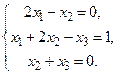 18.
18. 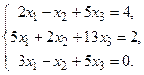
 20.
20. 
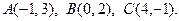 22.
22. 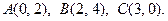
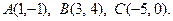 24.
24. 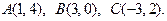
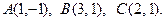 26.
26. 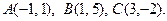
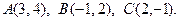 28.
28. 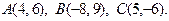
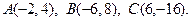 30.
30. 
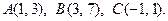 32.
32. 
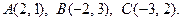 34.
34. 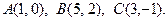
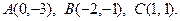 36.
36. 
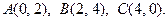 38.
38. 
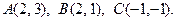 40.
40. 
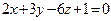 и плоскостью, проходящей через точки М 1, М 2, М 3.
и плоскостью, проходящей через точки М 1, М 2, М 3.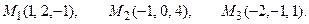



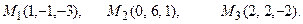
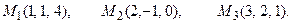
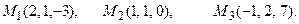
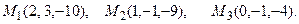

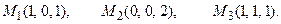
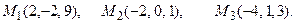
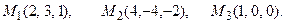
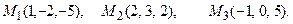
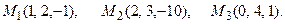
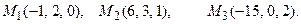
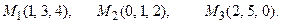
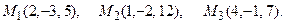
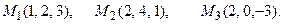

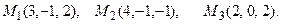
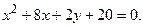
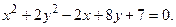
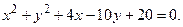
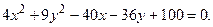

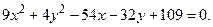
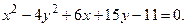

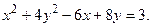
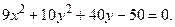


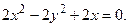
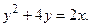

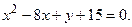
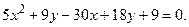



 ; б)
; б) 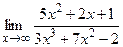 ;
;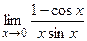 ; г)
; г) 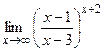 .
. ; б)
; б) 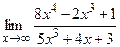 ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г) 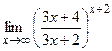 .
.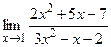 ; б)
; б)  ;
;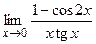 ; г)
; г) 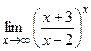 .
. ; б)
; б)  ;
;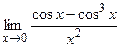 ; г)
; г)  .
.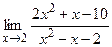 ; б)
; б)  ;
;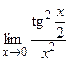 ; г)
; г) 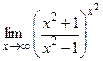 .
.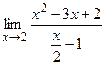 ; б)
; б) 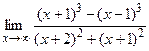 ;
; ; г)
; г)  .
.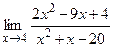 ; б)
; б) 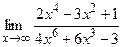 ;
;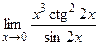 ; г)
; г) 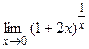 .
. ; б)
; б)  ;
;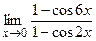 ; г)
; г) 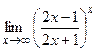 .
. ; б)
; б)  ;
;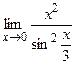 ; г)
; г)  .
. ; б)
; б) 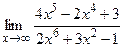 ;
; ; г)
; г)  .
. ; б)
; б)  ;
;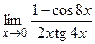 ; г)
; г)  .
.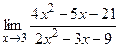 ; б)
; б)  ;
; ; г)
; г) 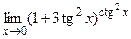 .
.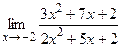 ; б)
; б) 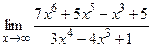 ;
; ; г)
; г) 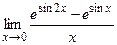 .
.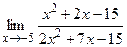 ; б)
; б) 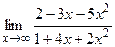 ;
; ; г)
; г)  .
. ; б)
; б) 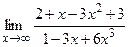 ;
;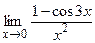 ; г).
; г). 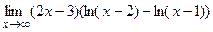 .
.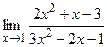 ; б)
; б)  ;
; ; г).
; г).  .
.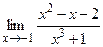 ; б)
; б) 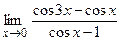 ;
; ; г).
; г). 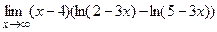 .
. ; б)
; б) 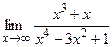 ;
;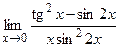 ; г).
; г).  .
. ; б)
; б)  ;
;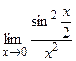 ; г).
; г). 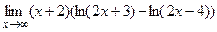 .
. ; б)
; б) 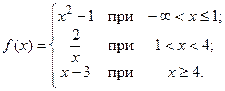
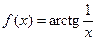 ; б)
; б) 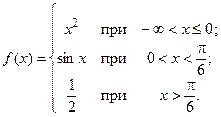
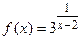 ; б)
; б) 
 ; б)
; б) 
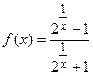 ; б)
; б) 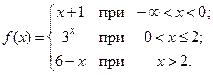
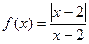 ; б)
; б) 
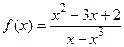 ; б)
; б) 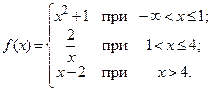
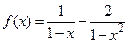 ; б)
; б) 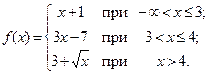
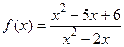 ; б)
; б) 
 ; б)
; б) 
 ; б)
; б) 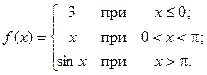
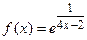 ; б)
; б) 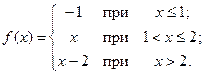
 ; б)
; б) 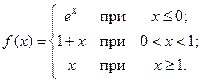
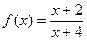 ; б)
; б) 
 ; б)
; б) 
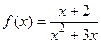 ; б)
; б) 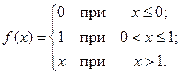
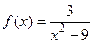 ; б)
; б) 
 ; б)
; б) 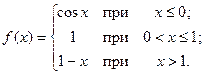
 ; б)
; б) 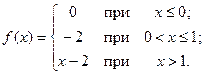
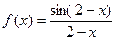 ; б)
; б) 
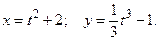
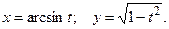

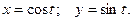


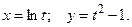

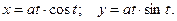
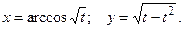
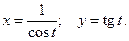
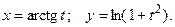
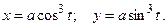
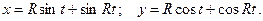
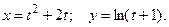
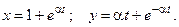
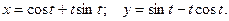


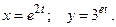
 .
. 142.
142. 
 144.
144. 
 146.
146. 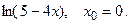
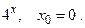 148.
148. 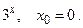
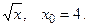 150.
150. 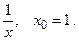
 152.
152. 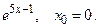
 154.
154. 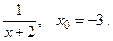
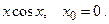 156.
156. 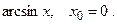
 158.
158. 
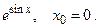 160.
160. 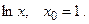
 162.
162.  163.
163. 
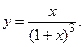 165.
165. 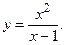 166.
166. 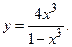
 168.
168. 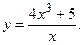 169.
169. 
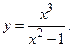 171.
171. 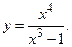 172.
172. 
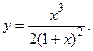 174.
174. 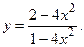 175.
175. 
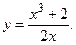 177.
177. 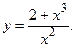 178.
178. 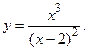
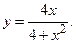 180.
180. 
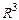 ...............
...............






