
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
По работе над курсом высшей математикиСодержание книги
Поиск на нашем сайте
Введение
Настоящее издание является методическим руководством для изучения общего курса высшей математики студентами-заочниками инженерно-технических специальностей. Оно является переработан-ным и дополненным вариантом изданий 1999 и 2002 годов. В пособии содержатся общие рекомендации студенту-заочнику по работе над курсом высшей математики, приводятся правила выполнения и оформления контрольных работ, представлена программа курса высшей математики, соответствующая учебным планам для 1-го се-местра; изложены основные понятия, определения, теоремы и т.д. из курса высшей математики, приведены образцы решения типовых примеров и контрольная работа № 1. Определение номеров задач из контрольной работы производится следующим образом: номер первой задачи контрольной работы равен двум последним цифрам номера зачетной книжки студента; номера последующих задач получаются от прибавления к номеру предыдущей задачи числа 20. Если две последние цифры номера зачетной книжки составляют число, большее чем 20, то номер первой задачи будет равен номеру из двух последних цифр минус число, кратное 20. Например: Номер зачетной книжки Номера задач 301787/148 8, 28, 48 и т.д. 303797/121 14, 34, 54 и т.д. 301797/100 20, 40, 80 и т.д. 303797/106 6, 26, 46 и т.д.
ОБЩИЕ РЕКОМЕНДАЦИИ СТУДЕНТУ-ЗАОЧНИКУ ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ КОНТРОЛЬНЫХ РАБОТ
При выполнении контрольных работ необходимо строго придер-живаться указанных ниже правил. Работы, выполненные без соблю-дения этих правил, не зачитываются и возвращаются студенту для переработки. 1. Каждая контрольная работа должна быть выполнена в отдельной тетради в клетку чернилами любого цвета, кроме красного. Необходимо оставлять поля шириной 4–5 см для замечаний рецензента. 2. В заголовке работы на обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер (шифр), название дисциплины, номер контрольной работы, номер варианта; здесь же следует указать название учебного заведения, дату отсылки работы в университет и адрес студента. В конце работы следует поставить дату ее выполнения и подпись студента. 3. В работу должны быть включены все задачи, указанные в задании, строго по положенному варианту. Контрольные работы, содержащие не все задачи, а также задачи не своего варианта, не зачи-тываются. 4. Решения задач надо располагать в порядке возрастания их номеров, указанных в заданиях, сохраняя номера задач. 5. Перед решением каждой задачи надо полностью выписать ее условие. В том случае, если несколько задач, из которых студент выбирает задачи своего варианта, имеют общую формулировку, сле-дует, переписывая условие задачи, заменить общие данные конкрет-ными, взятыми из соответствующего номера. Условие задачи должно быть написано так:
Найти работу, произведенную силой
Р е ш е н и е ______________________________________________________________________________________________________________________________________________________________________________
Ответ: А = 10.
6. Решения задач следует излагать подробно и аккуратно, кратко и лаконично объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи. Каждую задачу желательно начинать с новой страницы. 7. После получения прорецензированной работы, как не зачтенной, так и зачтенной, студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить все рекомендации рецензента. Если рецензент предлагает внести в решение задач те или иные исправления и дополнения, то в случае не зачтенной контрольной работы ее следует представить на повторную рецензию в короткий срок. При повторном представлении работы должна обязательно нахо-диться прорецензированная работа и рецензия на нее. Поэтому при выполнении контрольной работы рекомендуется оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений в соответствии с указаниями рецензента.
ПРОГРАММА
Элементы линейной алгебры И аналитической геометрии
1. Системы координат на прямой, плоскости и в пространстве. Про-странства 2. Скалярное произведение векторов и его свойства. Длина вектора и угол между двумя векторами в координатной форме. Условие ортогональности двух векторов. Механический смысл скалярного произведения. 3. Определители второго и третьего порядков, их свойства. Алгебраические дополнения и миноры. Определители n -го порядка. Вы-числение определителя разложением по строке (столбцу). 4. Векторное произведение двух векторов, его свойства. Условие коллинеарности двух векторов. Геометрический смысл определителя второго порядка. Простейшие приложения векторного произведения в науке и технике: моменты сил, сила, действующая на проводник с током в магнитном поле, скорость точки вращающегося тела, направление распространения электромагнитных волн. 5. Смешанное произведение векторов. Геометрический смысл оп-ределителя третьего порядка. 6. Уравнения линий на плоскости. Различные формы уравнения прямой на плоскости. Угол между прямыми. Расстояние от точки до прямой. 7. Кривые второго порядка: окружность, эллипс, гипербола, пара-бола, их геометрические свойства и уравнения. Технические прило-жения геометрических свойств кривых (использование фокальных свойств, математические модели формообразования биологических, технических и других объектов). 8. Уравнения плоскости и прямой в пространстве. Угол между плос-костями. Угол между прямыми. Угол между прямой и плоскостью. 9. Уравнение поверхности в пространстве. Цилиндрические поверхности. Сфера. Эллипсоид. Гиперболоиды. Параболоиды. Геомет-рические свойства этих поверхностей, исследование их формы методом сечений. Технические приложения геометрических свойств поверхностей (использование фокальных свойств, модели строитель-ных конструкций, физические модели элементов и т.п.). 10. Полярные координаты на плоскости. Спираль Архимеда. 11. Цилиндрические и сферические координаты в пространстве. Различные способы задания линий и поверхностей в пространстве. 12. Матрицы, действия с ними. Понятие обратной матрицы. 13. Системы двух и трех линейных уравнений. Матричная запись системы линейных уравнений. Правило Крамера. Система m линейных уравнений с n неизвестными. Метод Гаусса. Нахождение обратной матрицы методом Гаусса. 14. Пространство 15. Линейные и квадратичные формы в 16. Понятие линейного (векторного) пространства. Вектор как эле-мент линейного пространства. Примеры. Линейные операторы. При-меры линейных операторов. Применение линейных операторов для моделирования различных процессов.
Одной переменной
25. Понятие функции, дифференцируемой в точке, его геометрический смысл. Дифференциал функции. Общее представление о методах линеаризации. 26. Производная функции, ее смысл в различных задачах. Правила нахождения производной и дифференциала. 27. Производная сложной и обратной функции. Инвариантность формы дифференциала. Дифференцирование функций, заданных па-раметрически. 28. Точки экстремума функции. Теорема Ферма. 29. Теоремы Ролля, Лагранжа, Коши и их применение. 30. Производные и дифференциалы высших порядков. 31. Правило Лопиталя. 32. Формула Тейлора с остаточным членом в форме Пеано и форме Лагранжа. Представление функций Матрицы
Прямоугольная таблица из чисел вида
состоящая из m строк и n столбцов, называется матрицей размеров m ´ n. Матрица
где Если матрица А – вырожденная Пример 4.1. Найти матрицу
Так как
Следовательно,
Матричный метод. Решение невырожденной системы (4.1) можно найти по формуле Метод последовательного исключения неизвестных (метод Гаусса). С помощью элементарных преобразований над строками система m линейных уравнений с n неизвестными может быть приведена к виду
где Система (4.2) эквивалентна исходной системе. Если хотя бы одно из чисел
Пример 4.2. Методом Гаусса решить систему
Решение. Расширенная матрица системы имеет вид
Производя элементарные преобразования над строками расширенной матрицы, получаем
где цифрами
Этой матрице соответствует система
Отсюда последовательно находим
Ответ:
Пример 4.3. Решить систему уравнений
используя формулы Крамера. Решение. Так как определитель данной системы
то матрица А невырождена и система имеет единственное решение. Находим определители
По формулам Крамера находим решение системы:
4.3. Скалярное произведение векторов в R 3
Скалярным произведением векторов Свойства скалярного произведения: 1. 3. Свойство 4 выражает условие ортогональности векторов. Если векторы Из этой формулы и определения скалярного произведения следует:
Учитывая, что
Пример 4.4. Даны векторы
Решение.
Поскольку
а векторы
Поэтому
Механический смысл скалярного произведения: работа А, про-изводимая силой Прямая на плоскости. В декартовой прямоугольной системе координат Оxy прямая на плоскости может быть задана уравнениями: – общее уравнение прямой
Ax + By + C = 0; (4.3)
– уравнение прямой, проходящей через точку M 0(x 0, y 0)перпендикулярно нормальному вектору
A (x – x 0) + B (y – y 0) = 0;
– уравнение прямой, проходящей через точку M 0(x 0, y 0)параллельно направляющему вектору
– параметрические уравнения прямой
– уравнение прямой в отрезках
Здесь a и b – величины отрезков, отсекаемых на осях координат Ox и Oy (т.е. длины, взятые с соответствующими знаками); – уравнение прямой, проходящей через две данные точки M 1(x 1, y 1) и M 2(x 2, y 2):
– уравнение прямой с угловым коэффициентом k, проходящей через точку M 0(x 0, y 0):
y – y 0 = k(x – x 0).
Расстояние
Две прямые, заданные уравнениями A 1 x + B 1 y + C 1 = 0и A 2 x +
Пример 4.7. Составить уравнение прямой на плоскости, проходящей через точку М (–1, 2) перпендикулярно вектору, проходящему через точки М 1(3, 1) и М 2(4, –2). Найти расстояние от точки М до прямой, проходящей через точки М 1и М 2.
Решение. Уравнение прямой запишем в виде:
A (x – x 0) + B (y – y 0) = 0,
где x 0, y 0– координаты точки М, а А и В – координаты нормального вектора. Так как Для нахождения расстояния от точки М до прямой М 1 М 2 запишем уравнение этой прямой в виде
или 3 x + y – 10 = 0.
Подставляя в формулу (4.4) координаты x 0 = –1, y 0 = 2 точки М, получаем
2. Плоскость. Плоскость в прямоугольной системе координат мо-жет быть задана уравнениями:
Ax + By + Cz + D = 0 – общее уравнение плоскости. (4.5) Если в уравнении (4.5) отсутствует свободный член D, то плоскость проходит через начало координат; если в уравнении (4.5) отсутствует одна из переменных, то плоскость параллельна той оси, название которой не входит в это уравнение;
A (x – x 0) + B (y – y 0) + C (z – z 0) = 0 –
уравнение плоскости, проходящей через точку М 0(x 0, y 0, z 0) перпендикулярно нормальному вектору
где а, b, c – величина отрезков, отсекаемых плоскостью на координатных осях; – уравнение плоскости, проходящей через три данные точки M 1(x 1, y 1, z 1), M 2(x 2, y 2, z 2), M 3(x 3, y 3, z 3):
Величина угла φмежду двумя плоскостями A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z +D 2 = 0 вычисляется по формуле
Условие перпендикулярности данных плоскостей запишется в виде
Условие параллельности рассматриваемых плоскостей имеет вид
Расстояние
Пример 4.8. Cоставить уравнение плоскости, проходящей через точки М 1(1, 0, –1), М 2(2, –3, 0), М3(4, 7, 1).
Решение. Воспользуемся формулой (4.6):
Раскрыв определитель, получаем искомое уравнение плоскости:
13 x – y – 16 z – 29 = 0.
Линии второго порядка
Линией второго порядка называется множество точек плоскости, координаты x, y которых в прямоугольной системе координат удовлетворяют уравнению второй степени
Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0. (4.7)
Уравнение (4.7) называется общим уравнением линии второго порядка (А, В, С не равны нулю одновременно). При помощи преобразования прямоугольной системы координат (параллельного переноса и поворота) всегда можно найти такую новую прямоугольную систему координат, в которой уравнение (4.7) имеет один из следующих трех видов (каноническое уравнение):
где a, b, p – положительные числа. Уравнение (4.7) может определять так называемую вырожденную кривую (пустое множество, точ-ку, прямую, пару прямых). При этом линия, приводимая к виду (4.8), (4.9), (4.10), называется соответственно эллипсом, гиперболой или параболой. Эллипс с каноническим уравнением
Рис. 4.4
Точки F 2(– с, 0) и F 1(с, 0), где Числа а и b называются полуосями эллипса. Гипербола с каноническим уравнением
Рис. 4.5 Гипербола имеет две оси симметрии (координатные оси), с одной из которых (осью абсцисс) она пересекается в двух точках А 1(а,0), А 2(– а, 0), называемых вершинами гиперболы. Числа a и b – полуоси гиперболы: а – действительная полуось, b – мнимая. Точки F 2(– c, 0) и F 1(c, 0), где Парабола с каноническим уравнением
Рис. 4.6
Число p называется параметром параболы, точка О – ее вершиной, а ось Оx – осью параболы, вектор
Пример 4.9. Упростить уравнение
Решение. Выделим полные квадраты по переменным x и y соответственно.
Обозначая х – 3 = X, y + 1 = Y, получим каноническое уравнение эллипса
Рис. 4.7
Поверхности второго порядка
Поверхностью второго порядка называется множество точек про-странства, координаты x, y, z которых в прямоугольной системе координат удовлетворяют уравнению второй степени:
Уравнение (4.11) называется общим уравнением поверхности второго порядка (коэффициенты A, B, C, D, E, F не равны нулю одновременно). Если поверхность невырожденная, то при помощи преобразования прямоугольных координат (параллельного переноса и поворота) всегда можно найти такую новую систему координат, в которой уравнение (4.11) имеет один из следующих видов (каноническое уравнение):
В уравнениях (4.12)–(4.20) a, b, c, p положительны. Пример 4.10. Построить тело, ограниченное поверхностями
Решение. Тело ограничено снизу поверхностью параболоида:
Тело изображено на рис. 4.8.
Рис. 4.8
Пример 4.11. Построить тело, ограниченное поверхностями
Решение. Поверхность
Рис. 4.9
ОДНОЙ ПЕРЕМЕННОЙ
Дифференцирование функций
Производной функции y = f(x) в точке х называется предел отношения приращения функции к приращению аргумента, когда при-ращение аргумента стремится к нулю:
где
Производная обозначается у', y' (x), y'x.
Правила дифференцирования функций. Пусть С – постоянная, а u(x) и v(x) – дифференцируемые функции. Тогда C' = 0,
Производная сложной функции y = f (u (x)). Если функция u = u (x) дифференцируема в точке х, а функция y = f(u) дифференцируемая в соответствующей точке u = u (x), то сложная функция y = f (u (x)) дифференцируема в точке х и ее производная равна
Таблица производных.
1. 2. 3. 4. 5. 6.
7. 8. ( 9. 10. 11. 12.
13. 14.
Функция Для вычисления производной функции, заданной неявно, следует тождество
Пример 6.1. Найти производную показательно-степенной функции
Решение. Логарифмируя, а затем дифференцируя левую и правую части, получим
Умножая обе части равенства на у, имеем:
Пример 6.2. Найти производную функции
Решение. Дифференцируя по х тождество
Дифференциал При достаточно малых Пример 6.3. Найти приближенное значение объема шара, радиус которого равен 1,02 м.
Решение. Воспользуемся формулой
Приложение теорем Ролля, Лагранжа, Коши. Правило Лопиталя 1. Теорема Ролля. Если функция 2. Теорема Лагранжа. Если функция 3. Теорема Коши. Если функции
Пример 6.8. Доказать, что уравнение
Решение. Поскольку функция Тогда по теореме Ролля на интервале
Пример 6.9. Используя формулу Лагранжа, доказать неравен-ство
Решение. Функция
Пример 6.10. Написать формулу Коши и найти значение Решение. Все условия теоремы Коши выполнены:
Правило Лопиталя (раскрытие неопределенностей Пусть
Теорема. Пусть функции
Если | ||
|
| Поделиться: |

 , если ее точка приложения перемещается из точки
, если ее точка приложения перемещается из точки  в точку
в точку 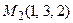 .
.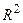 и
и  . Векторы. Линейные операции над векторами. Проекция вектора на ось. Направляющие косинусы и длина вектора. Понятие о векторных диаграммах в науке и технике (диаграммы сил, моментов сил, электрических токов, напряжений и др.). Координаты центра масс.
. Векторы. Линейные операции над векторами. Проекция вектора на ось. Направляющие косинусы и длина вектора. Понятие о векторных диаграммах в науке и технике (диаграммы сил, моментов сил, электрических токов, напряжений и др.). Координаты центра масс. . Линейные операции над векторами. Различ-ные нормы в
. Линейные операции над векторами. Различ-ные нормы в 
 по формуле Тейлора. Применение формулы Тейлора.
по формуле Тейлора. Применение формулы Тейлора. ,
,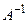 называется обратной к квадратной матрице А, если
называется обратной к квадратной матрице А, если  , где Е – единичная матрица. Для невырожденной матрицы
, где Е – единичная матрица. Для невырожденной матрицы 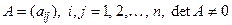 , где
, где 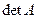 – определитель матрицы А, существует единственная обратная матрица
– определитель матрицы А, существует единственная обратная матрица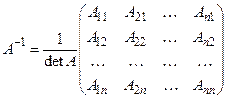 ,
, – алгебраические дополнения элементов
– алгебраические дополнения элементов  матрицы А.
матрицы А.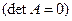 , то обратной к ней не существует.
, то обратной к ней не существует. .
. , то
, то  – невырожденная и
– невырожденная и  ;
;
 .
. .
. , (4.2)
, (4.2)
 отлично от нуля, то система (4.2), а следовательно, и исходная система несовместны. Если же
отлично от нуля, то система (4.2), а следовательно, и исходная система несовместны. Если же 
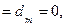 то система совместна и из уравнений (4.2) выражают последовательно неизвестные
то система совместна и из уравнений (4.2) выражают последовательно неизвестные  через
через  .
.
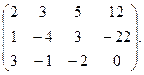

 обозначены следующие операции:
обозначены следующие операции: – первую и вторую строки поменяли местами;
– первую и вторую строки поменяли местами; 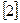 – ко второй строке прибавили первую, умноженную на (–2); к третьей прибавили первую, умноженную на (–3);
– ко второй строке прибавили первую, умноженную на (–2); к третьей прибавили первую, умноженную на (–3);  – к третьей строке прибавили вторую, умноженную на (–1).
– к третьей строке прибавили вторую, умноженную на (–1).
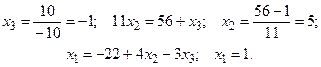






 и
и  называется число, обозначаемое
называется число, обозначаемое  или
или  и равное
и равное  где
где  – угол между
– угол между  2.
2. 
 4.
4. 
 и
и  представлены своими координатами в ортонормированном базисе
представлены своими координатами в ортонормированном базисе 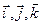 , то скалярное про-изведение равно
, то скалярное про-изведение равно 

 где
где  – проекция вектора
– проекция вектора  скалярное произведение векторов
скалярное произведение векторов  можно записать в виде
можно записать в виде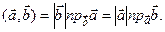
 Найти
Найти  .
.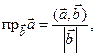
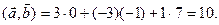

 точка приложения которой перемещается из точки
точка приложения которой перемещается из точки  в точку
в точку  вычисляется по формуле
вычисляется по формуле 
 :
: (каноническое уравнение прямой):
(каноническое уравнение прямой):
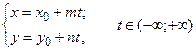 ;
;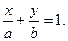
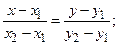
 от точки M 0(x 0, y 0) до прямой l, заданной уравнением (4.3), определяется по формуле
от точки M 0(x 0, y 0) до прямой l, заданной уравнением (4.3), определяется по формуле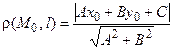 . (4.4)
. (4.4) , и перпендикулярны, если A 1 A 2 + B 1 B 2 = 0.
, и перпендикулярны, если A 1 A 2 + B 1 B 2 = 0.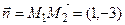 , то уравнение имеет вид 1(x + 1) –
, то уравнение имеет вид 1(x + 1) – 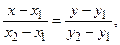 т.е.
т.е. 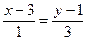 ,
,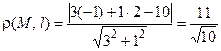 .
.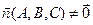 ;
;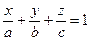 – уравнение плоскости в отрезках,
– уравнение плоскости в отрезках,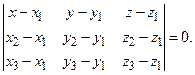 (4.6)
(4.6)
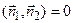 или
или 

 от точки M 0(x 0, y 0, z 0) до плоскости
от точки M 0(x 0, y 0, z 0) до плоскости 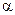 , заданной уравнением (4.5), вычисляется по формуле
, заданной уравнением (4.5), вычисляется по формуле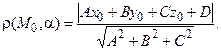
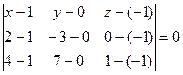 или
или 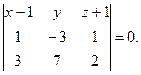
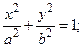 (4.8)
(4.8)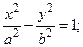 (4.9)
(4.9)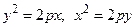 , (4.10)
, (4.10)
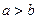 , имеет форму, изображенную на рис. 4.4.
, имеет форму, изображенную на рис. 4.4.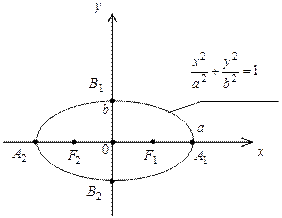
 называются фокусами эллипса.
называются фокусами эллипса. имеет форму, изображенную на рис. 4.5.
имеет форму, изображенную на рис. 4.5.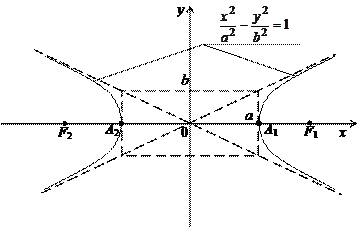
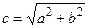 , называются фокусами гиперболы.
, называются фокусами гиперболы.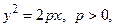 имеет форму, изображенную на рис. 4.6.
имеет форму, изображенную на рис. 4.6.

 – фокальный радиус-вектор точки М. Прямая
– фокальный радиус-вектор точки М. Прямая  называется директрисой параболы.
называется директрисой параболы.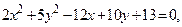 пользуясь переносом начала координат. Построить линию, определяемую этим уравнением.
пользуясь переносом начала координат. Построить линию, определяемую этим уравнением.
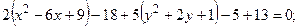
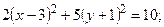

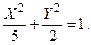 Начало новой системы координат – точка О 1(3, –1); оси ОX, ОY параллельны осям Оx и Оy соответственно. Большая полуось эллипса
Начало новой системы координат – точка О 1(3, –1); оси ОX, ОY параллельны осям Оx и Оy соответственно. Большая полуось эллипса  , малая полуось
, малая полуось 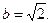 Изобразим кривую на рис. 4.7.
Изобразим кривую на рис. 4.7.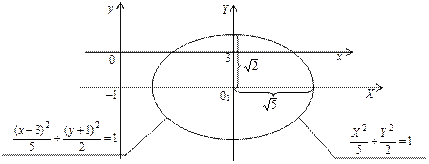
 (4.11)
(4.11)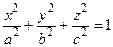 – эллипсоид; (4.12)
– эллипсоид; (4.12) – однополостный гиперболоид; (4.13)
– однополостный гиперболоид; (4.13)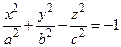 – двухполостный гиперболоид; (4.14)
– двухполостный гиперболоид; (4.14) – конус; (4.15)
– конус; (4.15)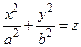 – эллиптический параболоид; (4.16)
– эллиптический параболоид; (4.16)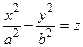 – гиперболический параболоид; (4.17)
– гиперболический параболоид; (4.17)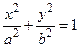 – эллиптический цилиндр; (4.18)
– эллиптический цилиндр; (4.18)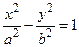 – гиперболический цилиндр; (4.19)
– гиперболический цилиндр; (4.19)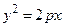 – параболический цилиндр. (4.20)
– параболический цилиндр. (4.20)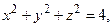
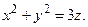
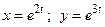 , а сверху – поверхностью сферы
, а сверху – поверхностью сферы 
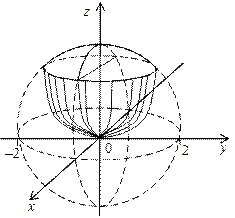
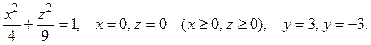
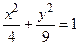 – эллиптический цилиндр. Он пересечен плоскостями х = 0, z = 0 (координатные плоскости Ozy и Оxy). По оси Оy тело ограничено плоскостями y = 3, y = –3 (рис. 4.9).
– эллиптический цилиндр. Он пересечен плоскостями х = 0, z = 0 (координатные плоскости Ozy и Оxy). По оси Оy тело ограничено плоскостями y = 3, y = –3 (рис. 4.9).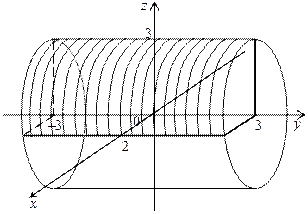



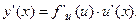






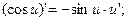







 неявно задана уравнением
неявно задана уравнением  если для всех
если для всех  выполняется равенство
выполняется равенство 
 продифференцировать по х (рассматривая левую часть как сложную функцию от х), а затем полученное уравнение решить относительно f'(x).
продифференцировать по х (рассматривая левую часть как сложную функцию от х), а затем полученное уравнение решить относительно f'(x). .
.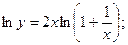

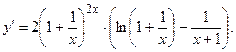
 , заданной неявно уравнением
, заданной неявно уравнением 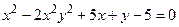 .
.
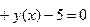 , получим
, получим  . Выражая
. Выражая  из этого равенства, находим:
из этого равенства, находим: .
. функции
функции 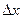 независимой переменной:
независимой переменной:  или
или 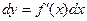 .
. , т.е.
, т.е.  или
или  .
. . Тогда
. Тогда 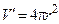 . Полагая
. Полагая  , получим
, получим 
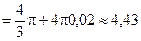 м3.
м3. непрерывна на отрезке
непрерывна на отрезке  , дифференцируема на интервале
, дифференцируема на интервале  и
и  , то существует хотя бы одна точка
, то существует хотя бы одна точка 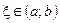 такая, что
такая, что  .
. такая, что
такая, что  (формула Лагранжа).
(формула Лагранжа). непрерывны на отрезке
непрерывны на отрезке  , то существует точка
, то существует точка  (формула Коши).
(формула Коши). имеет только один действительный корень.
имеет только один действительный корень.
 непрерывна и на концах отрезка
непрерывна и на концах отрезка  принимает значение разных знаков
принимает значение разных знаков  , то по первой теореме Больцано–Коши на интервале
, то по первой теореме Больцано–Коши на интервале  уравнение
уравнение  имеет корень. Предположим, от противного, что это уравнение имеет два действительных корня
имеет корень. Предположим, от противного, что это уравнение имеет два действительных корня 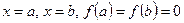 .
. существовала бы точка
существовала бы точка  , в которой
, в которой  . Но
. Но  при действительных
при действительных  . Полученное противоречие доказывает, что действительный корень – единственный.
. Полученное противоречие доказывает, что действительный корень – единственный.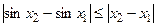 .
. удовлетворяет условиям тео-ремы Лагранжа на любом отрезке
удовлетворяет условиям тео-ремы Лагранжа на любом отрезке  . Поэтому
. Поэтому  . Отсюда, учитывая, что
. Отсюда, учитывая, что  , имеем
, имеем  .
. на отрезке
на отрезке  .
. . Поэтому
. Поэтому
 и
и  ).
). – окрестность точки
– окрестность точки 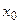 с выброшенной точки
с выброшенной точки  ;
;  .
.


