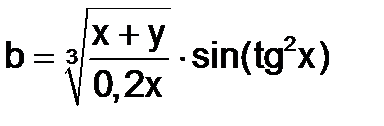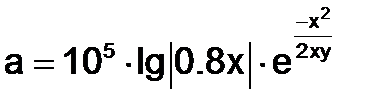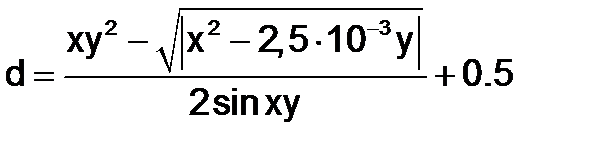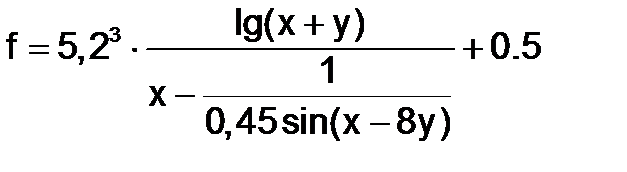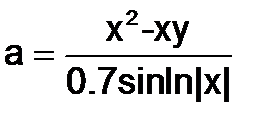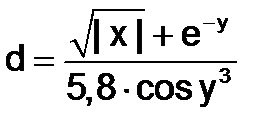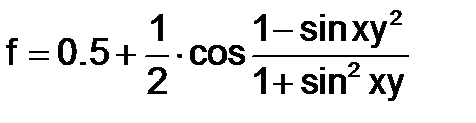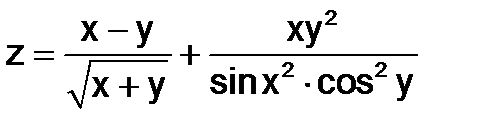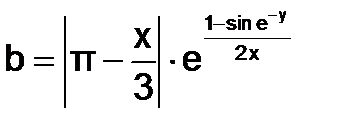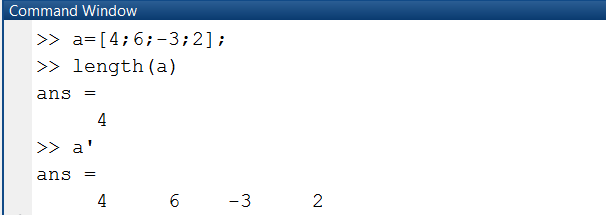Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Последние четыре операции, так называемые операции с точкой, осуществляют поэлементные операции над массивами.Содержание книги
Поиск на нашем сайте
Таблица 1.1.2-2
Подробнее операции над векторами и матрицами рассмотрены в Теме 1.2.
Приоритет исполнения математических операций в Matlab аналогичен приоритету в языках программирования высокого уровня: возведения в степень, умножения и деления, сложения и вычитания. Для изменения приоритета в математических выражениях используются круглые скобки. Функции – это имеющие уникальные имена объекты, выполняющие определенные преобразования своих аргументов (параметров) и при этом возвращающие результаты этих преобразований. Возврат результата – отличительная черта функций. Функции могут быть встроенными (внутренними) функциями системы Matlab, функциями пользователя, которые могут дополнять встроенные функции и описанные конкретным пользователем для своих нужд, внешними функциями, или m-функциями. Matlab обладает большим набором элементарных встроенных (библиотечных) функций, в том числе математических. Встроенные функции хранятся в откомпилированном виде в ядре системы Matlab. Некоторые из них приведены в табл. 1.1.2-3. Таблица 1.1.2-3
Система Matlab содержит более 1000 встроенных функций, однако предоставляет пользователю средства для создания и использования своих собственных функций – так называемых функций пользователя. О создании и использовании функций в виде m-файлов речь пойдет в параграфе 1.1.3. Рассмотрим несколько примеров (рис. 1.1.2-1).
Рис. 1.1.2-1. Примеры использования встроенных функций Matlab
Кроме математических выражений в Matlab используются логические выражения. Логические выражения в Matlab строятся на основе математических выражений, операций отношения и соответствующих им функций, логических операций и функций, а также круглых скобок. Результатом логического выражения является значение равное 1, если выражение Истинно (True), и значение 0 в противном случае – выражение Ложно (False). Если операнды – действительные числа, то использование операций тривиально. Операции отношения и соответствующие им функции служат для сравнения двух величин, векторов и матриц. Список операций отношений приведен в табл. 1.1.2-4. Таблица 1.1.2-4
Операции отношений выполняют поэлементное сравнение векторов или матриц одинакового размера и возвращают значение равное 1, если элементы идентичны, и значение 0 в противном случае.
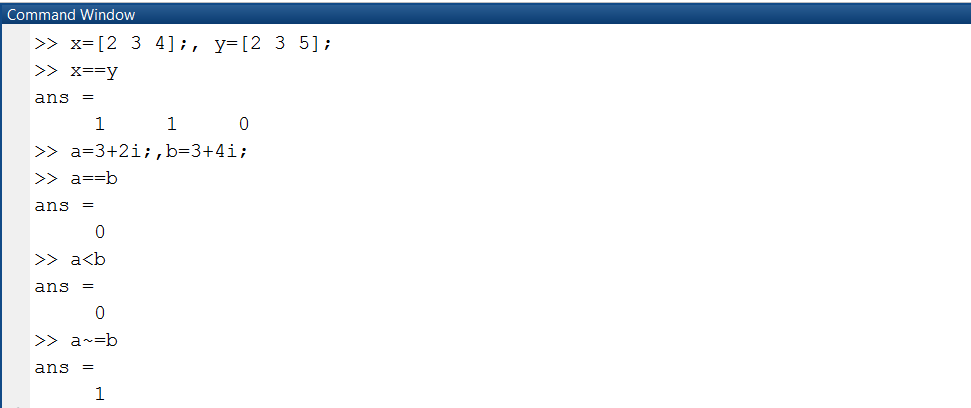
Следует отметить, что операции <, <=, >, >= при комплексных операндах используются для сравнения только действительных частей операндов – мнимые отбрасываются. В то же время операции == и ~= ведут сравнения с учетом как действительной, так и мнимой частей операндов (рис. 1.1.2-2).
Рис. 1.1.2-2. Примеры операций отношения над векторами и комплексными числами
Операции отношения обычно применяются в логических выражениях, которые являются условиями операторов if, for, while, switch и служат для изменения последовательности выполнения операторов программы Matlab.Использование этих операторов подробно рассмотрено в Теме 1.3. При вычислении выражений операции отношений имеют более низкий приоритет, чем арифметические, но более высокий, чем логические операции. Логические операции и соответствующие им функции служат для поэлементных логических операций над элементами одинаковых по размеру массивов. Список логических операций отношений приведен в Таблица 1.1.2-5
Логические функции дополняют логические операции и представлены в табл. 1.1.2-6, где в примерах используются вектора x=[1 0 0] и y=[111]. Таблица 1.1.2-6
Специальные операции реализуются с помощью специальных символов (табл. 1.1.2-7). Они предназначены для создания самых разнообразных объектов входного языка системы Matlab и придания им различных форм. Таблица 1.1.2-7
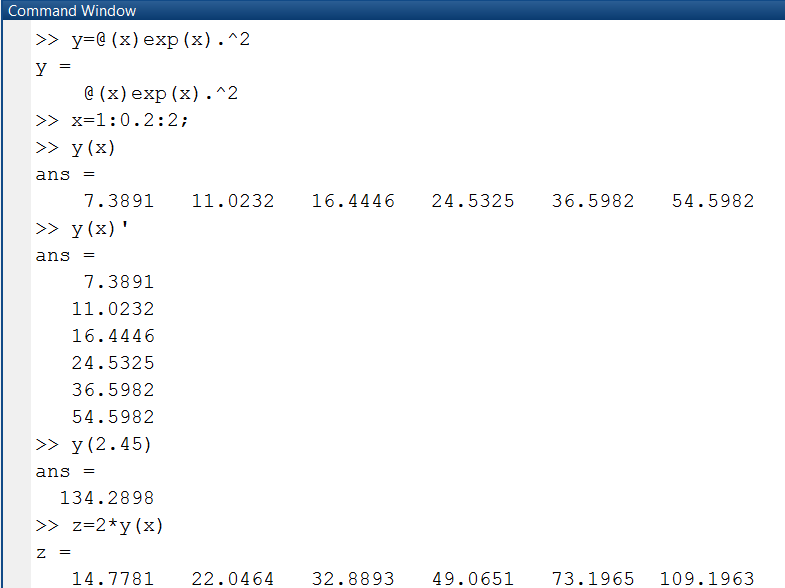
Функции пользователя – это функции, создаваемые пользователем системы, которые значительно облегчают работу за счет частого использования в математических выражениях, получении таблиц значений функций и построении графиков. Как правило, функции создаются для обработки множества значений аргументов, поэтому при описании их математических выражений используются операции с точкой. Для создания функции с помощью оператора @ используется следующий формат: Имя = @( Аргументы ) Выражение Функция может иметь несколько аргументов, тогда они перечисляются через запятую. Имя функции формируется аналогично имени переменной и должно быть уникально. Если в конце строки не введен символ точки с запятой, то в следующей строке выводится выражение функции. В примере (рис. 1.1.2-3) описана функция Для создания функции с использование inline() применяется следующий формат: Имя = inline (' Выражение ') Здесь выражение заключено в апострофы, а аргумент функции inline() символьный. Функция сама распознает аргументы и выводит в следующей строке принятое обращение. В приведенном ниже примере (рис. 1.1.2-4) показано описание функции с использованием inline(), вычисление значения функции s(x,y) для аргументов, заданных числами, и для аргументов, являющихся векторами. В последнем случае векторы, являющиеся аргументами функции, должны быть одной длины.
Рис. 1.1.2-3. Создание функции с помощью оператора @
Рис. 1.1.2-4. Создание функции с помощью inline() Наряду с рассмотренными выше функциями пользователя в Matlab имеется возможность создания функций (или некоторой последовательности вычислений) в виде m-файлов, которые можно сохранять и использовать в других сеансах работы. Подробнее материал о создании и работе с m-файлами, а также о средствах программирования в среде Matlab, изложен в Теме 3.1.
Символьная константа – это последовательность символов, заключенных в одиночные апострофы. Например, 'Кафедра ВМиП' Комментарии в Matlab определяются с помощью символа %. Например, % Это комментарий 1.1.3. Лабораторная работа по теме
Вопросы, подлежащие изучению
1) Элементы основного окна Matlab. 2) Окно панели Command Window. 3) Установка свойств среды системы Matlab. 4) Основные объекты системы Matlab. 5) Правила записи и вычисления арифметических выражений. 6) Работа с функциями пользователя, заданными в окне Command 7) Окна Workspace и Command History.
2. Общее задание
1) Изучите материал Темы 1.1 (п.п. 1.1.1 – 1.1.2). 2) Настройте стандартную конфигурацию Рабочей среды, выполнив команду Default. 3) Выполните команду clear all для очистки Рабочей среды. 4) Выберите вариант задания формул из табл. 1.1.3-1. 5) Задайте переменным x и y допустимые числовые значения. 6) Проанализируйте информацию, возникшую в окне Workspace. 7) Введите формулу для вычислений арифметического выражения и получите результат. 8) Измените значения исходных данных. 9) Измените формат вывода результата, выполнив команду 10) Верните формат вывода данных short. 11) Представьте арифметическое выражение в виде правой части функции f(x). 12) Опишите функцию f(x) с помощью оператора @, и получите вначале ее символьное выражение, а затем ее числовое значение при новом значении переменной х. 13) Опишите функцию f(x) с помощью inline(). 14) Измените значение переменной y, вычислите значения выражения b и функции f(x). 15) Объясните, почему изменение значения y привело к изменению значения b, но не повлияло на значение функции. 16) Задайте диапазон изменения аргумента функции с шагом, позволяющим получить таблицу значений функции f(x) для заданных значений аргумента (порядка 8-10 точек), и выведете значения функции f(х) в выбранном интервале вначале в строку, а затем в столбец. 17) Выполните команду who и проанализируйте выведенную информацию о данных. 18) Выполните команду whos и проанализируйте выведенную информацию о данных. 19) Установите путь к папке, находящейся на вашей флешь-карте, для сохранения содержимого окна Command Window. 20) Создайте файл в текущей папке. 21) Выделите в окне Command Window с использованием команд diary on и diary off область сохранения. 22) Сохраните текст рабочего окна на внешнем носителе. 23) Представьте результаты работы преподавателю, ответьте на поставленные вопросы. 24) Выполните команду clear all для очистки Рабочей среды. 25) Оформите отчет по выполненной работе. Варианты индивидуальных заданий
Таблица 1.1.3-1
Содержание отчета
1) В начале сессии введите в формате комментариев: · название лабораторной работы; · ФИО студента, номер группы; · № варианта; · индивидуальное задание. 2) Протокол вычислений (сессии) в окне Command Window в соответствии с общим заданием, снабженный подробными комментариями.
1.1.4. Контрольные вопросы по теме 1) Назначение окна Command Window. 2) Назначение окна Command History. 3) Окно отображения информации о данных. 4) Назначение команд who и whos. 5) Каким образом установить формат для вывода числовых значений на экран? 6) Каким образом перенести командную строку из окна Command History в окно Command Windows? 7) Каким образом установить формат для вывода числовых значений на экран? 8) Форматы числовых данных в системе Matlab. 9) Что такое системные константы? 10) Что такое символьные константы? 11) Команда объявления символьных переменных. 12) Какой символ используется для определения комментария? 13) Какая из операций.* или * является операцией поэлементного умножения? 14) Какой символ предназначен для запрета вывода результата выполнения команды на экран? 15) Создание функций с помощью команды @. 16) Создание функции с помощью inline(). Тема 1.2. Векторы, матрицы и 1.2.1. Вектора и матрицы 1.2.2. Построение графиков и визуализация вычислений в системе MatLab 1.2.3. Лабораторная работа по теме 1.2.4. Контрольные вопросы по теме
Векторы и матрицы
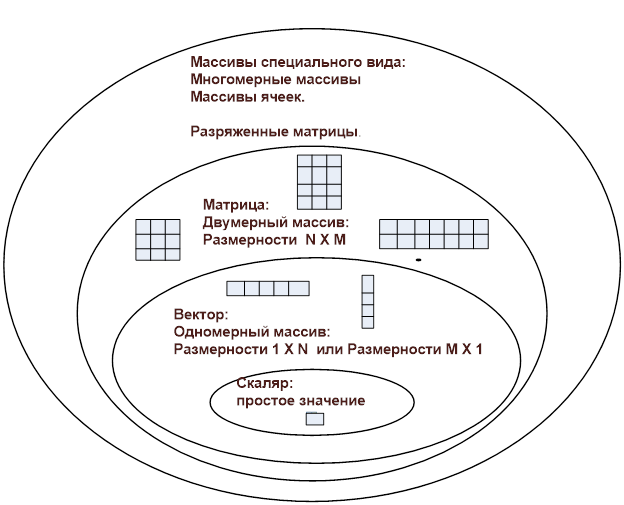
Matlab построена как система, ориентированная на работу с матрицами, то есть все численные вычисления производятся в матричной форме. Даже обычные числа и переменные в Matlab рассматриваются как матрицы размера 1 x 1. К особенностям работы с массивами в Matlab относится то, что одномерный массив может быть вектором-строкой или вектором-столбцом
Рис. 1.2.1-1. Представление данных в Matlab: переменные,
Для определения вектора используется операция квадратные скобки (операция объединения), а элементы вектора (рис. 1.2.1-2) отделяются друг от друга: · точкой с запятой, если нужно получить вектор-столбец; · пробелом или запятой, если нужно разместить элементы в векторе-строке.
Рис. 1.2.1-2. Создание вектора-строки a=[ ] и вектора-столбца b=[ ]
Для определения длины вектора используется функция length(а), где а – имя вектора, а для операции транспонирования используется символ апостроф (') (рис. 1.2.1-3).
Рис. 1.2.1-3. Определение длины вектора и его транспонирование
В следующем примере (рис. 1.2.1-4) при описании вектора х символ двоеточие, поставленный между двумя числами, указывает, что его элементы последовательно принимают значения, начиная от первого числа (0) до последнего числа (5) с шагом 1 (по молчанию шаг равен 1). При описании вектора y использован шаг 0.1, и выведены значения элементов вектора.
Рис. 1.2.1-4. Способы описания векторов с постоянным шагом
Для описания матрицы необходимо ввести ее имя и знак присваивания, а затем в квадратных скобках значения ее элементов. При этом значения элементов строк вводятся через пробел, а строки матрицы разделяет символ точка с запятой (;) (рис. 1.2.1-5):
А=[v1;v2;v3 ], где v1, v2, v3 - векторы одинаковой размерности.
Рис. 1.2.1-5. Создание матрицы A(3,4) и доступ к ее элементам
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1286; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.184.125 (0.013 с.) |


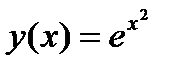 и получены ее значения для множества значений аргумента x. Традиционное обращение к функции выводит значения функции в строку, а добавление символа апостроф (') – в столбец. Также в примере показаны возможности вычисления значения функции от числового аргумента и использования функции пользователя в выражениях.
и получены ее значения для множества значений аргумента x. Традиционное обращение к функции выводит значения функции в строку, а добавление символа апостроф (') – в столбец. Также в примере показаны возможности вычисления значения функции от числового аргумента и использования функции пользователя в выражениях.