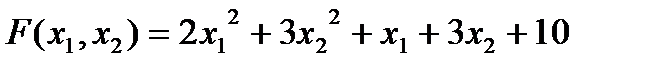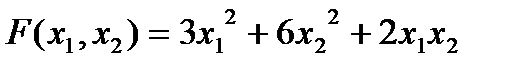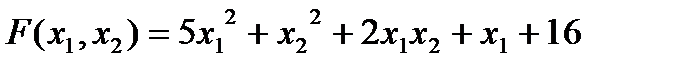Тема 2.6. Технология решения задач многомерной оптимизации

2.6.1. Решение задач многомерной оптимизации функций

2.6.2. Лабораторная работа по теме «Технология решения задач

многомерной оптимизации»

2.6.3. Контрольные вопросы по теме

Решение задач многомерной оптимизации

 

Задача, требующая нахождения оптимального значения функции m переменных Q(Х) = Q(x₁, x₂, …, x_m), называется задачей многомерной оптимизации. Так же, как и для случая одномерной оптимизации, задача нахождения максимума функции сводится к задаче нахождения минимума путем замены целевой функции Q на -Q.

В постановке задачи безусловной оптимизации для Q(Х)=Q(x₁,x₂,…,x_m) требуется найти хотя бы одну точку минимума Х* и вычислить Q*=f(Х*). Точка Х*Î R^m называется точкой глобального минимума функции Q на множестве Х, если для всех Х Î R^m выполняется неравенство Q(Х*) £ Q(Х). В этом случае значение Q(Х*) называется минимальным значением функции Q на R^m. Точка Х*ÎR^m называется точкой локального минимума функции Q, если существует такая d - окрестность U_d этой точки (d>0), что для всех Х Î Х_d = Х U_d выполняется неравенство Q(X*) £ Q(X).

Для всякой непрерывно дифференцируемой функции Q достаточным условием того, что функция имеет точку минимума, является положительная определенность матрицы вторых частных производных (матрицы Гессе):

Известно, что для того чтобы матрица была положительно определена, необходимо, чтобы все угловые миноры были положительны. Так, для функции двух переменных Q(x, y) матрица Гессе имеет вид:

,

а достаточным условием существования минимума является выполнение неравенств:

Аналитический метод поиска минимума применяется только для ограниченного круга задач. В основном это связано с необходимостью решения системы нелинейных уравнений, которая, как правило, решается численными методами. Гораздо проще решать задачу многомерной оптимизации численными методами, например, такими как метод градиентного спуска с дроблением шага и методы наискорейшего спуска с аналитическим или численным выбором шага [1].

 

Вычисление экстремума функции нескольких переменных

z = f(x₁, x₂, …x_n)

в MatLab осуществляет функция:

 

[X, Z] = fminsearch(name, x0),

где:

· name – имя функции, зависящее от n переменных;

· x0 – вектор из n элементов, содержащий координаты точки начального приближения;

· X – вектор из n элементов, содержащий координаты точки, в которой достигается минимум;

· Z – значение функции в точке с координатами X.

 

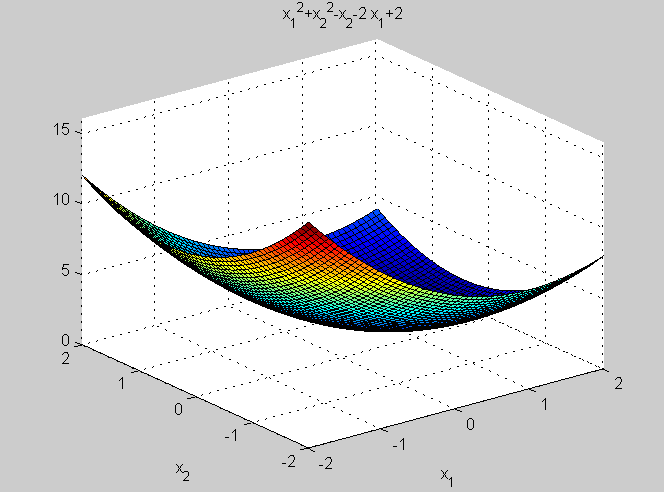
Рассмотрим работу функции fminsearch() на примере определения минимума двумерной функции f(x1, x2) = x₁² + x₂² - x₂ - 2x₁ + 2.

 

 

 

 

Рис. 2.6.1-1. Результат выполнения функции ezsurf()

 

Построим график (рис. 2.6.1-1) с использованием функции ezsurf(), аргументами которой служат: выражение функции, заключенное в одинарные кавычки, вектор изменения первой производной и вектор изменения второй переменной.

 

>> ezsurf ('x1.^2+x2.^2-x2-2*x1+2', [-2 2], [-2 2])

 

При нахождении минимума функции оформим многомерную функцию в виде m-функции (рис. 2.6.1-2).

 

 

Рис. 2.6.1-2. Целевая функция F(x)

 

Определим координаты точки минимума и значение функции в этой точке с использованием функции Matlab minsearch() (рис. 2.6.1-3).

 

 

Рис. 2.6.1-3. Использование функции fminsearch() для нахождения

минимума многомерной функции

 

Лабораторная работа по теме

«Технология решения задач многомерной оптимизации»

 

 

Вопросы, подлежащие изучению

 

1) Построение графиков функции от двух переменных F(x₁,х₂) средствами пакета Matlab.

2) Нахождение координат точки минимум функции F(x₁,х₂) с использованием встроенных функций пакета Matlab - fminsearch().

 

 

2. Общее задание

 

1) Изучите материал Темы 2.6 (п. 2.6.1).

2) Выберите индивидуальное задание из табл. 2.6.2-1.

3) Постройте график функции F(x₁,х₂).

4) Найдите координаты точки минимум функции F(x₁,х₂) с использованием встроенной функции fminsearch().

5) Получите значение функции в точке минимума.

6) Сохраните текст рабочего окна на внешнем носителе.

7) Представьте результаты работы преподавателю, ответьте на поставленные вопросы.

8) Выполните команду clear all.

9) Оформите отчет по выполненной работе.

Варианты индивидуальных заданий

 

Таблица 2.6.2-1

 

№	Функции для вычисления минимума

Содержание отчета

1) В форме комментариев:

· Название лабораторной работы

· ФИО студента, номер группы

· № варианта

· Индивидуальное задание

2) Протокол вычислений (сессии) в окне Command Window, снабженный необходимыми комментариями.

2.6.3. Контрольные вопросы по теме

 

1) Какую функцию называют многомерной?

2) Что является достаточным условием существования минимума для многомерной функции?

3) Назначение функции fminsearch(name, x0) и ее параметров.

4) Можно ли с использованием функции fminsearch() вычислить локальный максимум?

5) Что служит результатом выполнения функции fminsearch()?

6) Какие средства Matlab используются для описания целевой функции и как это влияет на параметры функции fminsearch()?

 

Список литературы

 

1. Васильев А.Н. Matlab. Самоучитель. Практический подход. – СПб.: Наука и Техника, 2012. – 448 с.

2. Дьяконов В.П. Полный самоучитель. – М.: ДМК Пресс, 2012.

3. Половко А.М., Бутусов П.Н. MATLAB для студентов. – СПб.: БХВ-Петербург, 2005. – 320 с., ил.

4. Кетков Ю.Л., Кетков А.Ю., Шульц М.М. Matlab 6.x: программирование численных методов. – СПб.: БХВ-Петербург, 2004. – 672 с., ил.

 

 

 

План УМД на 2016/17 уч.г.

 

 

Виктор Николаевич Шакин

Татьяна Игоревна Семенова

 

 

Основы работы с
математическим пакетом Matlab

Учебное пособие

 

Подписано в печать 2015г. Формат 60х90 1/16.

Объём 8,3 усл.п.л. Тираж экз. Изд. №. Заказ.

ООО «Брис-М». Москва, ул. Авиамоторная, д. 8а.