
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение графиков поверхностиСодержание книги Поиск на нашем сайте
I. Построение графика поверхности z=x2-y2 в диапазоне х Î[-2;2], y Î[-1;1] при шаге изменения аргументов D х= 0,2;D у= 0,2.
3.5.1. Провести табуляцию аргумента х: · ввести в А2 число –2; · ввести в А3 число –1,8; · выделить ячейки А2:А3; · поставить указатель мыши в правый нижний угол ячейки А3 (указатель примет вид тонкого крестика) и провести заполнение ячеек до А22. 3.5.2. Провести табуляцию аргумента у: · ввести в В1 число –1; · ввести в С1 число –0,8; · выделить ячейки В1:С1; · заполнить значениями аргумента у ячейки D1:L1.
3.5.3. Ввести формулы для вычисления Z: · ввести в ячейку В2 формулу =$A2^2-B$1^2; · скопировать формулу в ячейки В3:L22 и С2:L2. Для этого следует скопировать формулу в ячейки В3:В22, затем выделить ячейки В2:В22 и скопировать весь выделенный столбец в ячейки С2:L22. В результате получим табл. 7 (режим показа вычислений) и табл. 8 (часть табл. 7 в режиме показа формул). Таблица 7
Таблица 8
3.5.4. Построить график поверхности: а) Выполнить команды Вставка – Диаграмма – Поверхность – выбрать левый верхний тип поверхности (рис. 8) – Далее ( при работе с Excel 2007 команды Вставка - Другие диаграммы);
б) На втором шаге Мастера диаграмм: · ввести Диапазон данных В2:L22; · перейти на вкладку Ряд; · ввести Подписи оси Х А2:А22; · в поле Ряд выбрать Ряд 1, щелкнув по нему мышью; · щелкнуть по полю Имя, щелкнуть мышью по ячейке В1 (рис. 9); · в поле Ряд щелкнуть мышью по Ряд 2; · щелкнуть по полю Имя, щелкнуть мышью по ячейке С1. Аналогичным образом ввести Ряд Адрес ячейки Ряд 3 D1 Ряд 4 E1 ……………….. Ряд 11 L1, щелкнуть Далее.
в) На третьем шаге ввести название осей: Х, Y, Z и щелкнуть Далее.
г) На четвертом шаге выбрать опцию На отдельном листе и щелкнуть Готово.
В результате получим график поверхности (рис. 10).
Рис. 10. График функции z=x2-y2
3.5.5. Теперь построим график функции а) Добавить новый рабочий лист (Вставка – Лист) в открытой книге Excel; б) В ячейках А2:А12 провести табуляцию переменной х (аналогично п. 3.5.1); в) В ячейках В1:L1 провести табуляцию переменной y (аналогично п. 3.5.2); г) Для вычисления функции Z ввести формулы в ячейки В2:L22: · в ячейку В2 ввести формулу =КОРЕНЬ($A2^2+B$1^2+1); Можно для извлечения квадратного корня вместо функции КОРЕНЬ использовать возведение в дробную степень (1/2). Тогда формула будет выглядеть так: =($A2^2+B$1^2+1)^(1/2); · Скопируем формулу из В2 в В3:L12 и С2: L2 (аналогично п. 3.5.3);
4. Отчет по работе Распечатки диаграмм и графиков.
Литература: [3], с. 123-132.
Работа 3. Графическое решение уравнений и систем уравнений
Цель работы
Ознакомиться с графическими методами решения уравнений и систем уравнений.
Основные теоретические положения
Кроме аналитического способа решения уравнений f (x)=0 можно пользоваться и графическим способом. Графический способ наиболее эффективен для решения трансцендентных уравнений. При графическом способе для уравнения строится график y=f (x) и решением уравнения является точка пересечения графика с осью х при у =0. Если разбить уравнение на две произвольные части, то можно для каждой части построить график. В этом случае решением уравнения будет абсцисса точки пересечения графиков для этих частей. Такой способ может использоваться и для решения систем двух линейных уравнений с двумя неизвестными.
Порядок выполнения работы Задание 1. Решить графически уравнение y =cos2(p x) на интервале [0;1]. Задание 2. Решить графически уравнение х 3-4 х 2-3 х +6=0. Задание 3. Решить графически систему уравнений Задание 4. Решить систему уравнений согласно индивидуальному заданию.
3.1. Выполнение задания 1 Решить графически уравнение y =cos2(p x) на интервале [0;1] значит найти все значения х внутри данного интервала, где функция у пересекает ось Х.
3.1.1.Провести табуляцию значений х и у (см. Работу 2). В результате получим табл. 9.
3.2. Выполнение задания 2
Найдем графическое решение уравнения х 3-4 х 2-3 х +6=0. Для этого представим его в виде х 3=4 х 2+3 х -6 (2) и построим на одной диаграмме графики двух функций: у 1= х 3 левая часть уравнения (2) и у 2=4 х 2+3 х -6 правая часть уравнения (2)
Так как мы ищем корни кубического уравнения, число корней должно быть равно трем. Заранее значения корней неизвестны, поэтому сначала возьмем для построения графиков интервал х Î[-2;2], с шагом 0,4 и построим на этом интервале графики функций у 1 и у 2. Координаты точек х пересечения этих графиков дадут нам искомые значения корней.
Таблица 10
Рис. 15. Решение уравнения х 3-4 х 2-3 х +6=0.
3.2.3. Для нахождения третьего корня нужно увеличить диапазон решения. Из графика видно, что при х <-2 функции у 1 и у 2 расходятся. Значит, решение нужно искать при х >2. Увеличим диапазон до х =4,8, т. е. х Î[-2; 4,8]: а) продолжить табулирование аргумента х до ячейки А20; б) скопировать формулу из ячейки В13 в ячейки В14:В20; в) скопировать формулу из ячейки С13 в ячейки С14:С20; г) построить график для этого случая. На этом графике функции у 1 и у 2 пересекаются трижды. Третий корень х 3=4,4.
3.3. Выполнение задания 3 Решить графически систему уравнений значит найти координаты точек, в которых пересекаются графики функций, входящих в систему уравнений. При выполнении задания 2 мы решили практически систему уравнений
Для нахождения корней уравнений системы
в диапазоне х Î[0;3] с шагом D х =0,2, следует выполнить следующие действия.
3.3.1. Добавить новый рабочий лист
3.3.2. Провести табулирование переменных х, y =sin x, y =cos x, аналогично Работе 2 и пп. 3.1, 3.2 данной работы: - в ячейку А1 ввести заголовок Аргумент х, в ячейку А2 – значение 0, в ячейку А3 - значение 0,2 и провести табуляцию аргумента х в ячейках А2:А17; - в ячейку В1 ввести заголовок y =sin(x); - в ячейку В2 ввести формулу =SIN(A2) и скопировать ее в ячейки В3:В17; - в ячейку С1 ввести заголовок y =cos(x); - в ячейку С2 ввести формулу =COS(A2) и скопировать ее в ячейки C3:C17.
3.2.3. Построить график функций y =sin x, y =cos x на одной диаграмме: а) выполнить команды Вставка – Диаграмма (Вставка – График); б) в первом диалоговом окне Мастера диаграмм выберем Тип диаграммы График, Вид - Левый верхний, Далее; в) во втором окне Мастера диаграмм на вкладке Диапазон данных ввести: Диапазон В2:С17 Ряды в: столбцах; Затем щелкнуть по вкладке Ряд и ввести: Подписи оси Х А2:А17; Щелкнуть по кнопке Далее; г) в третьем окне Мастера диаграмм ввести: Название диаграммы Система Ось Х Аргумент Ось У Значения щелкнуть по кнопке Далее; д) на последнем шаге Мастера диаграмм выбрать опцию На отдельном листе и щелкнуть Готово. На полученном графике (рис. 16) видно, что в указанном диапазоне система имеет единственное решение (графики имеют только одну точку пересечения).
Рис. 16. Решение системы уравнений
Для нахождения решения: - поставить указатель мыши в точку пересечения графиков; - щелкнуть левой клавишей мыши. Появится надпись с указанием приблизительного решения системы уравнений: Ряд “y=cos(x)” Точка “0,8” Значение: 0,6967067 Следовательно, решением уравнения являются: х =0,8 у =0,697. 3.4. Выполнение задания 4
3.4.1. Выбрать из табл. 11 индивидуальное задание по указанию преподавателя.
3.4.2. Добавить новый рабочий лист. 3.4.3. Графически решить систему уравнений в указанном диапазоне с заданным шагом по индивидуальному заданию.
Таблица 11
Отчет по работе Распечатка графиков.
Литература: [3], с. 187-193. Работа 4. Приближенное решение уравнений
1. Цель работы
Изучение работы с процедурой Подбор параметра.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1107; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.166.207 (0.011 с.) |

 Рис. 8. Окно мастера диаграмм Excel
Рис. 8. Окно мастера диаграмм Excel
 Рис. 9. Построение диаграммы Поверхность
Рис. 9. Построение диаграммы Поверхность

 , где х Î[-5;5], y Î[-5;5]; D x =1; D y =1.
, где х Î[-5;5], y Î[-5;5]; D x =1; D y =1.
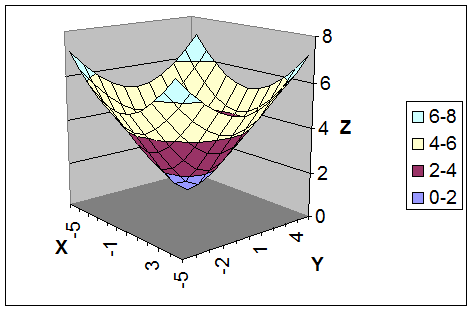 Рис. 13. График функции
Рис. 13. График функции  в диапазоне х Î[0;3] с шагом D х =0,2.
в диапазоне х Î[0;3] с шагом D х =0,2.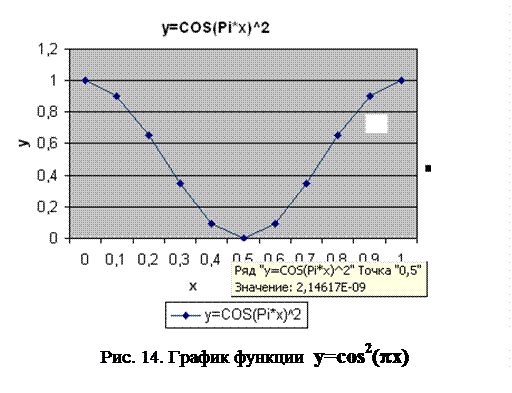

 .
.













